软件工程（2019）第三次作业

一、题目要求

题目(1)：最大连续子数组和（最大子段和）

（1）问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n。例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

（2）代码托管地址：https://dev.tencent.com/u/wyd76/p/zuoye/git/tree/master

代码如下：

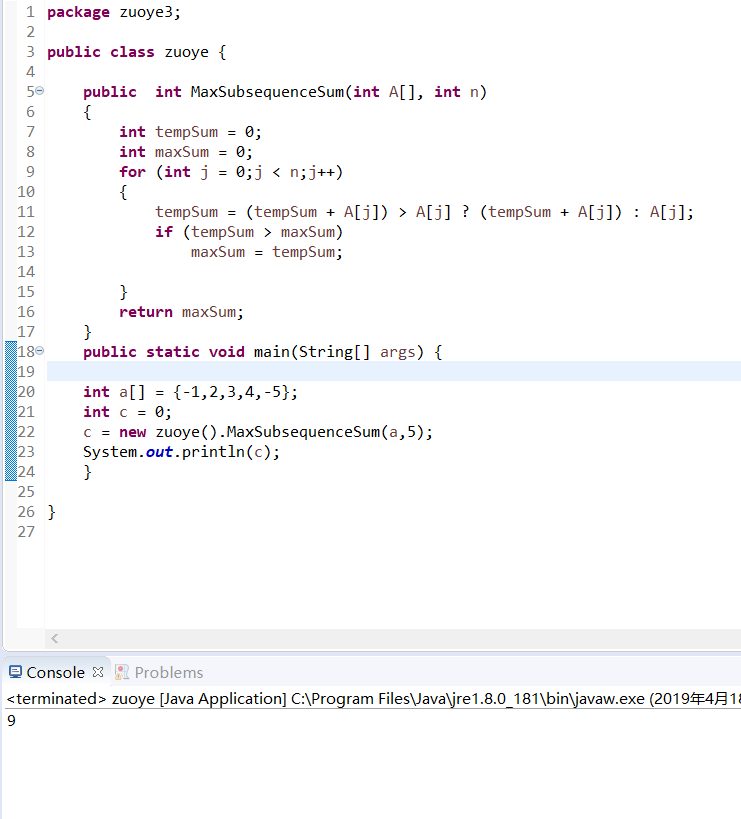
package zuoye3;

public class zuoye {
	
	public  int MaxSubsequenceSum(int A[], int n)
	{
	    int tempSum = 0;
	    int maxSum = 0;
	    for (int j = 0;j < n;j++)  
	    {
	        tempSum = (tempSum + A[j]) > A[j] ? (tempSum + A[j]) : A[j];
	        if (tempSum > maxSum) 
	            maxSum = tempSum;

	    }
	    return maxSum;
	}

}

（3）代码分析：只进行一次for循环，用tempSum接收前j项和第j项最大值，然后进入判断语句，比较得到的新的最大值与之前的最大值，更新maxSum的值。

二、用条件组合覆盖设计测试用例

（1）tempSum + A[j] > A[j]并且更新后tempSum > maxSum
（2）tempSum + A[j] > A[j]并且更新后tempSum <= maxSum
（3）tempSum + A[j] <= A[j]并且更新后tempSum > maxSum
（4）tempSum + A[j] <= A[j]并且更新后tempSum <= maxSum
测试用例1:a[ ] = { 1， -2， 3， -4， 5},覆盖了（2）（3）
测试用例2:a[ ] = {-1， 2， -3， 4， 5},覆盖了（1）（4）

三、单元测试

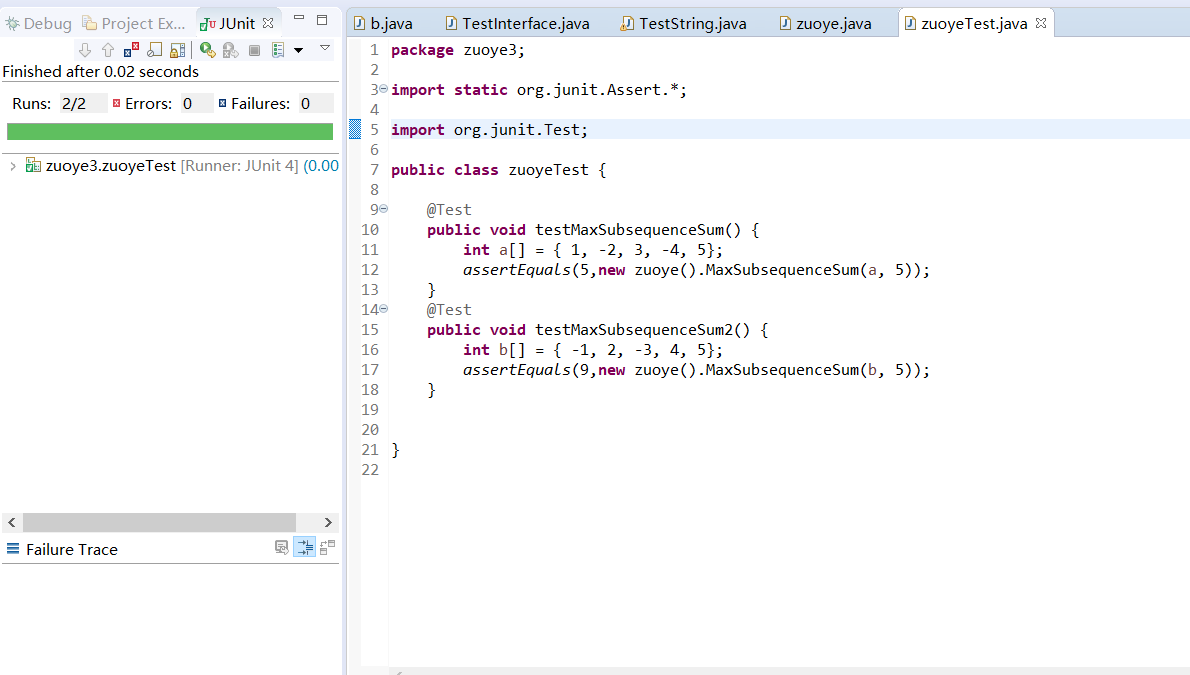
（1）代码如下

package zuoye3;

import static org.junit.Assert.*;

import org.junit.Test;

public class zuoyeTest {

	@Test
	public void testMaxSubsequenceSum() {
		int a[] = { 1, -2, 3, -4, 5};
		assertEquals(5,new zuoye().MaxSubsequenceSum(a, 5));
	}
	@Test
	public void testMaxSubsequenceSum2() {
		int b[] = { -1, 2, -3, 4, 5};
		assertEquals(9,new zuoye().MaxSubsequenceSum(b, 5));
	}
	

}

（2）单元测试截图

四、程序运行截图