Fibonacci 常见性质

Fibonacci 常见性质

参考：斐波那契数列的性质 - Milkor - 博客园

定义

\(f[1]=f[2]=1\)

\(f[i]=f[i-1]+f[i-2]\)

可以构造矩阵：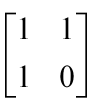
和矩阵：

二者乘积为：

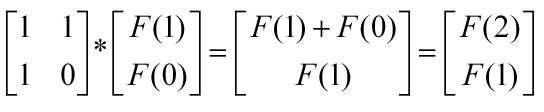
所以可以矩阵快速幂 \(log(n)\) 求 \(f[n]\)

性质

1. \(\gcd(f[i],f[i+1])=1\)

   证明：由辗转相除法：\(gcd(f[i],f[i+1])=gcd(f[i-1],f[i])=...=gcd(f[1],f[2])=1\)

2. \(f[m]=f[m-n+1]\times f[n]+f[m-n]\times f[n-1]\)

   证明：设 \(f[n]=a,f[n+1]=b\) ，有：\(f[n+2]=a+b\quad f[n+3]=a+2b\quad f[n+4]=2a+3b\)

   容易发现，\(f[n+x]\) 的系数为 \(f[x-1]\) 。

   衍生的，我们有：

   • 性质4
   • 取 \(m=2n\) 我们得到：\(f[2n]=(f[n+1]+f[n-1)\times f[n]\)
   • 归纳证明：\(\forall k\in N,f[n]|f[nk]\)
   • 可逆：\(\forall f[a]|f[b],a|b\)

3. \(\sum_{i=1}^nf[i]=f(n+2)-1\)

   发现，\(f[i+1]-f[i-1]=f[i]\) ，直接把每一项拆开即可。

   衍生的，我们有：

   • \(\sum_{i=1}^nf[i]^2=f[n]f[n+1]\)
   • \(\sum_{i=0}^{\lfloor n/2 \rfloor}f[2i+1]=f[2n]\)
   • \(\sum_{i=1}^{\lfloor n/2 \rfloor}f[2i]=f[2n+1]-1\)

4. \(\gcd(f[n],f[m])=f[\gcd(n,m)]\)

   证明：我们可以把 \(f[m]\) 通过性质2 拆开：

   \(\gcd(f[n],f[m])=\gcd(f[n],f[m-n+1]\times f[n]+f[m-n]\times f[n-1])\)

   \(=\gcd(f[n],f[m-n]\times f[n-1])=\gcd(f[m-n],f[n])=f[\gcd(n,m)]\)

   （其中其实还用到了性质一）