【图论】强联通分量

强联通分量(Tarjan)

　　什么是强联通分量？强联通分量就是在有向图中，每两个点都可以相互到达。

　　　  比如说下面这个图就是强联通分量：

 

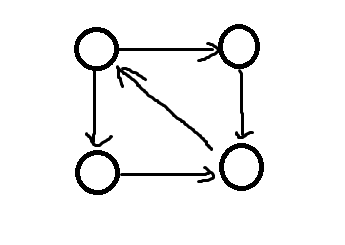
　　　　那么怎么求强联通分量呢？

　　　   我们设两个数组：dfn，low

　　　　dfn：i节点是第几个被访问到的

　　　　low：从i节点出发可以追溯到的dfn值最小的节点。

　　　　当low==dfn说明它就是一个强联通分量。

　　　　比如说：

　　　　

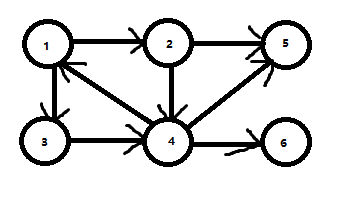
　　　　首先，1的dfn1=low1=1

　　　   然后访问到2，2的dfn2=low2=2

　　　   然后是5，5的dfn5=low5=3

　　　   回溯，访问到4，4的dfn4=low4=4

　　　   5已经访问过了，由5的dfn值更新4的low，low4=3

　　　   访问到1，由1的dfn值更新4的low，low4=1

　　　   访问到6，dfn6=low6=5

　　　   返回2，更新low2=min(low2,low4)=1

　　　　1访问3，low3=dfn3=6

　　　　4已经访问过了，用4的dfn更新3也就是low3=4

　　　　得出下表：

	dfn	low
1	1	1
2	2	1
3	6	4
4	4	1
5	3	3
6	5	5

 

 

 

 

 

　　　　那么就可以在这个过程中得出强联通分量了。

　　　   代码:

void Tarjan(int x){
	++tot; dfn[x]=low[x]=tot;
	vis[x]=true; que[++tmp]=x;
	for(int i=0;i<vec[x].size();i++){
		int to=vec[x][i];
		if(!dfn[to]){//继续访问 
			Tarjan(to);
			low[x]=min(low[x],low[to]);
		}
		else if(vis[to]) low[x]=min(dfn[to],low[x]);//更新low 
	}
	if(dfn[x]==low[x]){
		++Col; tar[x]=Col;//标记该点属于哪一个强联通分量 
		vis[x]=false;//退栈 
		while(que[tmp]!=x){//将这个强联通分量的点依次弹出 
			int k=que[tmp];
			tar[k]=Col; vis[k]=false;
			tmp--;
		}
		tmp--;
	}
}

　　　　　Tarjan的功能：①LCA

　　　　　　　　　　　  ②缩点(缩点后图成为DAG)    

　　　　　　　　　　　　例题：【图论】Popular Cows

　　　　　　　　　　　　　  【图论】The Bottom of a Graph

　　　　　　　　　　　 　 　【图论】Network of Schools