拓扑排序

差分约束

要求构造长度为 \(n\) 的序列使其满足 \(m\) 条形如 \(a_i - a_j \le x_k\) 或 \(a_i < a_j\) 的约束。

对于每个约束 \(a_i - a_j \le x_k\)（即 \(a_j + x_k \ge a_i\)）由 \(j\) 向 \(i\) 连一条边权为 \(x_k\) 的有向边，若图中存在负环，则无解。建立超级源点并向每个点连一条边权为 \(0\) 的边，再计算源点到每个点 \(u\) 的最短路 \(dis_u\)，\(a_u = dis_u\) 即为原约束的一组可行解。

特别地，若约束全部为 \(a_i < a_j\) 形式（即 \(x\) 全部为 \(1\)），由 \(i\) 向 \(j\) 连一条有向边，若图中存在环，则无解，否则构成一个有向无环图。设 \(f_v\) 为 \(a_v\) 的最小可能取值，则 \(f_v = \max \limits_{u \to v} f_u + 1\)。

[POI2015] PUS

线段树优化差分约束建图。注意只有叶子结点才会在转移时加 \(1\)，线段树上的虚点不影响。

反图逆向最大字典序

[HNOI2015] 菜肴制作

在 DAG 拓扑序中要求第 \(i\) 个数在前 \(i - 1\) 个数尽量优先的情况下尽量优先，最终答案就是反图中字典序最大的拓扑序的逆向序列。

二分图判定

如果要将图分为两个内部没有连边的部分，可以染色法判奇环。

P1330 封锁阳光大学

欧拉路径

欧拉回路

「连通无向图中所有点的度数为偶数」为「图中存在欧拉回路」的充分必要条件。

必要性：如果图中存在欧拉回路，那么回路上的点每被经过一次就会使其度数加 \(2\)。

充分性：构造性证明。每次在图中找出一个环，如果它是欧拉回路，结论成立。如果不是，就在图中删去这个环，所有点的度数依然是偶数，然后重新寻找环。因为图是连通的，所以每次找到的环与剩下的图都会有交集，可以连接起来形成一个回路。

同时也证明了，如果图中存在欧拉回路，那么图的边集可以划分为若干个简单环的并集。

欧拉通路

「连通无向图中度数为奇数的点个数为 \(0\) 或 \(2\)」为「图中存在欧拉通路」的充分必要条件。

必要性：如果图中存在欧拉通路，那么通路的起点和终点度数加 \(1\) ，其余点每次经过度数加 \(2\)。

充分性：将两个奇度数点相连，可以找到一条欧拉回路，再将连接的边断开，就形成了欧拉通路。

同理，如果一个连通图中有 \(k\) 个奇度数点（显然 \(k\) 为偶数），则可以用 \(\max(1, \frac{k}{2})\) 条欧拉通路覆盖所有边。

Hierholzer 算法

考虑通过递归简化寻找欧拉路径。

其实我们并不需要真正找出每一个环再合并，可以在 DFS 找回路的回溯过程中直接对回路上的每个点找回路。也就是说，将原本找回路的顺序倒过来，这样就没有必要显式地求出当前回路了，而是在回溯的过程中，一边对当前点找回路，一边往回路中插入当前回路。

[USACO3.3] 骑马修栅栏

void dfs(int u)
{
	for (int j = g.last[u]; j != -1; j = g.next[j])
	{
		g.last[u] = g.next[j];
		if (mark[j] == 0) mark[j] = mark[pos[e[j].id ^ 1]] = 1, dfs(g.to[j]);
	}
	ans.push(u);
}

并查集

一般用于维护集合中带有传递性的信息，在每个集合中用一个点上的信息统一代表一个集合。

也可以用于在树上将子节点与父亲节点合并以快速修改。

单调队列

如果状态转移都是由一段连续的状态中的最值得到，可以考虑用单调队列维护。

[SCOI2010] 股票交易

后两个可以分别通过单调队列维护。

[NOI2005] 瑰丽华尔兹

最小生成树

CF827D Best Edge Weight

每一条不在最小生成树上的边都会在最小生成树中形成一个环。如果非树边必须要在最小生成树中，它的边权就要小于环上所有边权的最小值。如果树边必须要在最小生成树中，它的边权就要小于所有覆盖它的非树边的权值的最小值。

同理，如果一条树边或非树边原本就满足条件，它就一定在最小生成树上。

Kruskal 重构树

加边时新建一个点权为所加边权的虚点代表大集合，将原来两个点所在的集合虚点设为左儿子和右儿子。

这样，从某节点只经过权值小于等于某个数的边所能到达的点就是重构树上的一棵子树。

线段树

线段树进阶

对于较复杂的线段树操作，需要注意每一次上传和下传标记时有没有将所有维护的值和标记对应修改，还有不同标记的关系和下放顺序。

[SCOI2010] 序列操作

可以发现，反转和赋值两种操作可以统一使用一个 tag。

#include <cstdio>
#include <algorithm>

const int maxn = 100000 + 10;

struct segmenttree
{
	struct node
	{
		int l, r;
		int cnt[2], left[2], right[2], mid[2];
		int tag;
	}
	T[maxn << 2];
	
	void rep(int p, int k)
	{
		if (k == 0 || k == 1)
		{
			T[p].tag = k;
			T[p].cnt[k]     = T[p].left[k]     = T[p].right[k]     = T[p].mid[k]     = T[p].r - T[p].l + 1;
			T[p].cnt[k ^ 1] = T[p].left[k ^ 1] = T[p].right[k ^ 1] = T[p].mid[k ^ 1] = 0                  ;
		}
		else if (k == 2)
		{
			T[p].tag ^= 1;
			std::swap(T[p].cnt[0], T[p].cnt[1]), std::swap(T[p].left[0], T[p].left[1]);
			std::swap(T[p].right[0], T[p].right[1]), std::swap(T[p].mid[0], T[p].mid[1]);
		}
	}
	
	void updata(int p)
	{
		for (int j = 0; j <= 1; j++)
		{
			T[p].cnt[j] = T[p << 1].cnt[j] + T[(p << 1) | 1].cnt[j];
			T[p].left[j]  = T[p << 1].left[j]        + T[(p << 1) | 1].left[j] * (T[p << 1].cnt[j ^ 1]       == 0);
			T[p].right[j] = T[(p << 1) | 1].right[j] + T[p << 1].right[j]      * (T[(p << 1) | 1].cnt[j ^ 1] == 0);
			T[p].mid[j] = std::max(T[p << 1].right[j] + T[(p << 1) | 1].left[j], std::max(T[p << 1].mid[j], T[(p << 1) | 1].mid[j]));
		}
	}
	
	void downdata(int p) { rep(p << 1, T[p].tag), rep((p << 1) | 1, T[p].tag), T[p].tag = 3; }
	
	void build(int p, int l, int r, int a[])
	{
		T[p].l = l, T[p].r = r, T[p].tag = 3;
		if (l == r) rep(p, a[l]), T[p].tag = 3;
		else build(p << 1, l, (l + r) >> 1, a), build((p << 1) | 1, ((l + r) >> 1) + 1, r, a), updata(p);
	}
	
	void modify(int p, int l, int r, int k)
	{
		if (T[p].l > r || T[p].r < l) return;
		else if (l <= T[p].l && T[p].r <= r) rep(p, k);
		else downdata(p), modify(p << 1, l, r, k), modify((p << 1) | 1, l, r, k), updata(p);
	}
	
	int cnt(int p, int l, int r)
	{
		if (T[p].l > r || T[p].r < l) return 0;
		else if (l <= T[p].l && T[p].r <= r) return T[p].cnt[1];
		else return downdata(p), cnt(p << 1, l, r) + cnt((p << 1) | 1, l, r);
	}
	
	int queryleft(int p, int r)
	{
		if (T[p].l > r) return 0;
		else if (T[p].r <= r) return T[p].left[1];
		else
		{
			downdata(p);
			if (r <= T[p << 1].r || T[p << 1].cnt[0]) return queryleft(p << 1, r);
			else return T[p << 1].left[1] + queryleft((p << 1) | 1, r);
		}
	}
	
	int queryright(int p, int l)
	{
		if (T[p].r < l) return 0;
		else if (T[p].l >= l) return T[p].right[1];
		else
		{
			downdata(p);
			if (l >= T[(p << 1) | 1].l || T[(p << 1) | 1].cnt[0]) return queryright((p << 1) | 1, l);
			else return T[(p << 1) | 1].right[1] + queryright(p << 1, l);
		}
	}
	
	int query(int p, int l, int r)
	{
		if (T[p].l > r || T[p].r < l) return 0;
		else if (l <= T[p].l && T[p].r <= r) return T[p].mid[1];
		else
		{
			downdata(p);
			int ans = std::max(query(p << 1, l, r), query((p << 1) | 1, l, r));
			if (l <= T[p << 1].r && r >= T[(p << 1) | 1].l) ans = std::max(ans, queryright(p << 1, l) + queryleft((p << 1) | 1, r));
			return ans;
		}
	}
}
T;

int a[maxn];

int main()
{
	int n, m;
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	T.build(1, 1, n, a);
	for (int i = 1; i <= m; i++)
	{
		int opt, l, r;
		scanf("%d %d %d", &opt, &l, &r), l++, r++;
		if (opt <= 2) T.modify(1, l, r, opt);
		else if (opt == 3) printf("%d\n", T.cnt(1, l, r));
		else printf("%d\n", T.query(1, l, r));
	}
	return 0;
}

线段树优化区间相关 DP

浅谈几类线段树、树状数组优化 DP - recollect_i - 洛谷博客

对于区间相关 DP，可以将区间按右端点排序，在每个区间的右端点处统计答案。

同时，如果转移方程是类似 \(f_i = \max\limits_{j = 1}^{i} f_j + \operatorname{g}(j, i)\) 的形式，可以用线段树维护 \(T_j\) 表示枚举到 \(i\) 时 \(f_j + \operatorname{g}(j, i)\) 的值，每次计算 \(f_i\) 时先更新 \(T_j\) 中 \(\operatorname{g}(j, i)\) 的值。

[USACO05DEC] Cleaning Shifts S

CF115E Linear Kingdom Races

\(f_i\) 表示在 \([1, i]\) 道路中能获得的最大利润。\(f_i = \max\limits_{j = 0}^{i - 1} f_j - \operatorname{cost}_{j + 1, i} + \operatorname{val}_{j + 1, i}\)。

使用线段树维护 \(T_j\) 表示当前 \(f_j - \operatorname{cost}_{j + 1, i} + \operatorname{val}_{j + 1, i}\) 的值。

依次枚举 \(i \in [1, n]\)，先更新 \(\operatorname{cost}_{j + 1, i}\) 的值，即 \(T_j \gets T_j - a_i (j \in [0, i - 1])\)，再更新 \(\operatorname{val}_{j + 1, i}\) 的值，即对于所有 \(r_k = i\) 更新 \(T_j \gets T_j + w_k (j \in [0, l_k - 1])\)。于是 \(f_i = \max(f_{i - 1}, \max\limits_{j = 0}^i T_j)\)，\(T_i \gets f_i\)。

最终答案即为 \(\max\limits_{i = 1}^n f_i\)。

AT_dp_w Intervals

[NOIP2023] 天天爱打卡

[ZJOI2010] 基站选址

标记永久化

不用上传和下传标记。

如果区间修改完全覆盖了某节点，就更新其 tag，否则正常更新。那么在每个节点的 tag 中保存的就是对其子树整体所做的修改。因此查询时需要同时维护该点所有祖先节点的 tag 的合并结果。

但是使用场景有限制，比如不能处理受顺序影响的标记。

同时，因为可持久化线段树和树套树等数据结构无法下传标记，所以也需要标记永久化。

「学习笔记」线段树标记永久化

zkw 线段树

不能优化时间复杂度的技巧都是奇技淫巧。需要结合标记永久化，除了卡常用处不大。

算法学习笔记(76): zkw线段树

算法学习——zkw线段树

zkw线段树 模板整理与例题

图的连通性

主打一个感性理解。

参考：Tarjan 论文，【洛谷日报#237】Tarjan，你真的了解吗？，图论基础 - Alex_Wei - 博客园。

强连通分量

wiki：

Each node v is assigned a unique integer v.index, which numbers the nodes consecutively in the order in which they are discovered. It also maintains a value v.lowlink that represents the smallest index of any node on the stack known to be reachable from v through v's DFS subtree, including v itself. Therefore v must be left on the stack if v.lowlink < v.index, whereas v must be removed as the root of a strongly connected component if v.lowlink == v.index. The value v.lowlink is computed during the depth-first search from v, as this finds the nodes that are reachable from v.

The lowlink is different from the lowpoint, which is the smallest index reachable from v through any part of the graph.

v.lowlink := min(v.lowlink, w.index) is the correct way to update v.lowlink if w is on stack. Because w is on the stack already, (v, w) is a back-edge in the DFS tree and therefore w is not in the subtree of v. Because v.lowlink takes into account nodes reachable only through the nodes in the subtree of v we must stop at w and use w.index instead of w.lowlink.

DeepL 翻译：

每个节点 v 都有一个唯一的整数 v.index，它按照节点被发现的顺序连续编号。它还会维护一个值 v.lowlink，该值代表栈中已知可通过 v 的 DFS 子树（包括 v 本身）从 v 到达的任何节点的最小索引。因此，如果 v.lowlink < v.index 则 v 必须留在堆栈上，而如果 v.lowlink == v.index 则 v 必须作为强连接组件的根节点被删除。v.lowlink 的值是在从 v 开始的深度优先搜索中计算出来的，因为这样可以找到从 v 可以到达的节点。

lowlink 与 lowpoint 不同，后者是 v 通过图的任何部分可到达的最小索引。

如果 w 在栈上，则 v.lowlink := min(v.lowlink, w.index) 是更新 v.lowlink 的正确方法。由于 w 已在堆栈上，(v, w) 是 DFS 树中的后沿，因此 w 不在 v 的子树中。由于 v.lowlink 考虑了只能通过 v 子树中的节点到达的节点，因此我们必须在 w 处停止更新，并使用 w.index 代替 w.lowlink。

虽然我看不懂，但总之 zhw 讲的是错的。差评。

int dfn[maxn], low[maxn], dfx = 0;
int scc[maxn], scccnt = 0;
std::stack<int> stack;

void tarjan(int u)
{
	dfn[u] = low[u] = ++dfx;
	stack.push(u);
	for (int j = g.last[u]; j != 0; j = g.next[j])
	{
		int v = g.to[j];
		if (dfn[v] == 0) tarjan(v), low[u] = std::min(low[u], low[v]);
		else if (scc[v] == 0) low[u] = std::min(low[u], dfn[v]);
	}
	if (dfn[u] == low[u])
	{
		scccnt++;
		while (1)
		{
			int t = stack.top();
			stack.pop();
			scc[t] = scccnt;
			if (t == u) break;
		}
	}
	return;
}

每个强连通分量中任意两个点都可以互相到达，缩点后形成有向无环图，可以进行 DP。计数、概率题记得判重边。

有时可能会发现题目最后需要求每个点在 DAG 中可达点个数，可以考虑在缩点前的图中发现性质，比如可到达的点都是一段连续区间，就可以在 DP 过程中转移左端点和右端点。

割点和桥

如图，无向图中只存在树边和返祖边，不存在前向边和横叉边。返祖边和被返祖边覆盖的树边都不是桥。

也因为非树边都是返祖边，所以求 Tarjan 割点和桥时不需要栈。

int dfn[maxn], low[maxn], dfx = 0;
bool cut[maxn], bridge[maxm];

void dfs(int u, int fa)
{
	dfn[u] = low[u] = ++dfx;
	int son = 0;
	for (int j = g.last[u]; j != 0; j = g.next[j])
	{
		int v = g.to[j];
		if (v == fa) continue;
		if (dfn[v] == 0)
		{
			son++;
			dfs(v, u);
			low[u] = std::min(low[u], low[v]);
			if (low[v] >= dfn[u]) cut[u] = 1;
			if (low[v] > dfn[u]) bridge[(j + 1) / 2] = 1;
		}
		else low[u] = std::min(low[u], dfn[v]);
	}
	if (fa == 0) cut[u] = son >= 2;
}

[AHOI2005] 航线规划

使用树链剖分动态维护两点间桥的数量。因为只有不被非树边覆盖的树边是桥，所以可以维护区间内被覆盖次数的最小值和个数。

点双连通分量

每个割点会处于多个点双中，每条边则会处于唯一的点双。

找出点双有两种写法，洛谷题解区常见的一种是找出每个点所在的点双，但因为割点会处于多个点双，所以出栈时不能弹出其本身。

int dfn[maxn], low[maxn], dfx = 0;
std::stack<int> stack;
std::vector<std::vector<int>> vdcc;

void tarjan(int u, int fa)
{
	dfn[u] = low[u] = ++dfx;
	if (g.last[u] == 0) { vdcc.push_back({u}); return; }
	stack.push(u);
	for (int j = g.last[u]; j != 0; j = g.next[j])
	{
		int v = g.to[j];
		if (v == fa) continue;
		if (dfn[v] == 0)
		{
			tarjan(v, u);
			low[u] = std::min(low[u], low[v]);
			if (low[v] >= dfn[u])
			{
				std::vector<int> t;
				t.push_back(u);
				int top;
				do top = stack.top(), t.push_back(top), stack.pop();
				while (top != v);
				vdcc.push_back(t);
			}
		}
		else low[u] = std::min(low[u], dfn[v]);
	}
}

for (int i = 1; i <= n; i++) if (dfn[i] == 0) tarjan(i, 0);

又因为每条边都处于一个唯一的点双，也可以找出每条边所在的点双，再转换到点上。

int dfn[maxn], low[maxn], dfx = 0;
std::stack<int> stack;
bool mark[maxm];
std::vector<std::set<int>> vdcc;

void tarjan(int u, int fa)
{
	dfn[u] = low[u] = ++dfx;
	if (g.last[u] == 0) { vdcc.push_back({u}); return; }
	for (int j = g.last[u]; j != 0; j = g.next[j])
	{
		int v = g.to[j];
		if (mark[(j + 1) / 2] == 0) stack.push((j + 1) / 2), mark[(j + 1) / 2] = 1;
		if (v == fa) continue;
		if (dfn[v] == 0)
		{
			tarjan(v, u);
			low[u] = std::min(low[u], low[v]);
			if (low[v] >= dfn[u])
			{
				std::set<int> t;
				int top;
				do top = stack.top(), stack.pop(), t.insert(g.st[top * 2 - 1]), t.insert(g.to[top * 2 - 1]);
				while (top != (j + 1) / 2);
				vdcc.push_back(t);
			}
		}
		else low[u] = std::min(low[u], dfn[v]);
	}
}

for (int i = 1; i <= n; i++) if (dfn[i] == 0) tarjan(i, 0);

虽然第二种写法比较冷门，但实际上更好用，因为点的信息不好转移到边上，但边的信息可以转移到点。

将每一个割点与其每一个所在的点双连边，缩边后形成 Block-Cut Tree（不是圆方树）。树上点双和割点交替出现。

[POI2008] BLO-Blockade

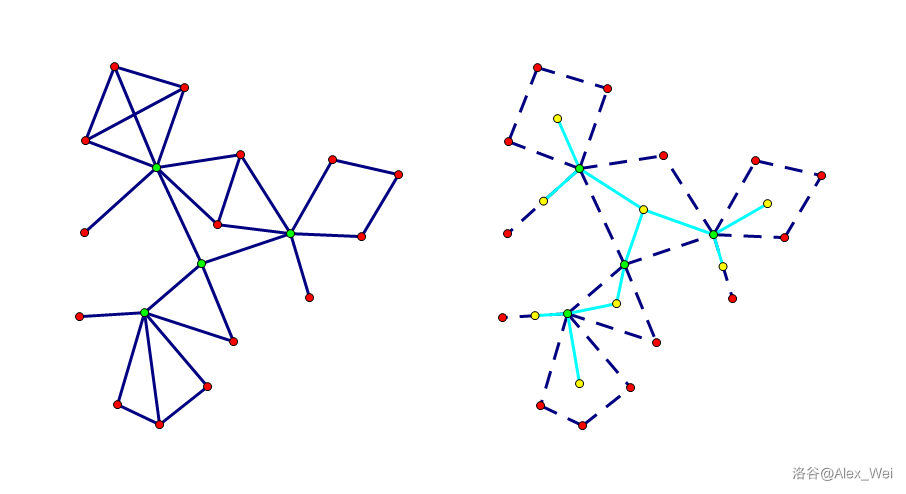
如果封锁某个非割点城镇，不会发生的访问活动为 \(2 \times (n - 1)\) 个。如果封锁割点城市 \(u\)，依旧会发生的访问活动就只能在各个连通块中单独举行。因为割点会处于多个点双中，所以在统计某节点的子树大小时要减去它的子节点个数。

[HNOI2012] 矿场搭建

非割点坍塌没有影响，为避免割点坍塌只需要在点双缩点树上的每个叶子节点中任选一个设置救援出口。特别地，如果连通块本身就没有割点，需要两个救援出口。

边双连通分量

每个点都属于一个唯一的边双连通分量。记得判重边。

int dfn[maxn], low[maxn], dfx = 0;
std::stack<int> stack;
std::vector<std::vector<int>> edcc;

void tarjan(int u, int fa)
{
	dfn[u] = low[u] = ++dfx;
	if (g.last[u] == 0) { edcc.push_back({u}); return; }
	stack.push(u);
	for (int j = g.last[u]; j != 0; j = g.next[j])
	{
		int v = g.to[j];
		if ((j + 1) / 2 == fa) continue;
		if (dfn[v] == 0)
		{
			tarjan(v, (j + 1) / 2);
			low[u] = std::min(low[u], low[v]);
			if (low[v] > dfn[u]) 
			{
				std::vector<int> t;
				int top;
				do top = stack.top(), stack.pop(), t.push_back(top);
				while (top != v);
				edcc.push_back(t);
			}
		}
		else low[u] = std::min(low[u], dfn[v]);
	}
}

for (int i = 1; i <= n; i++) if (dfn[i] == 0)
{
	tarjan(i, 0);
	if (!stack.empty())
	{
		std::vector<int> t;
		while (!stack.empty()) t.push_back(stack.top()), stack.pop();
		edcc.push_back(t);
	}
}

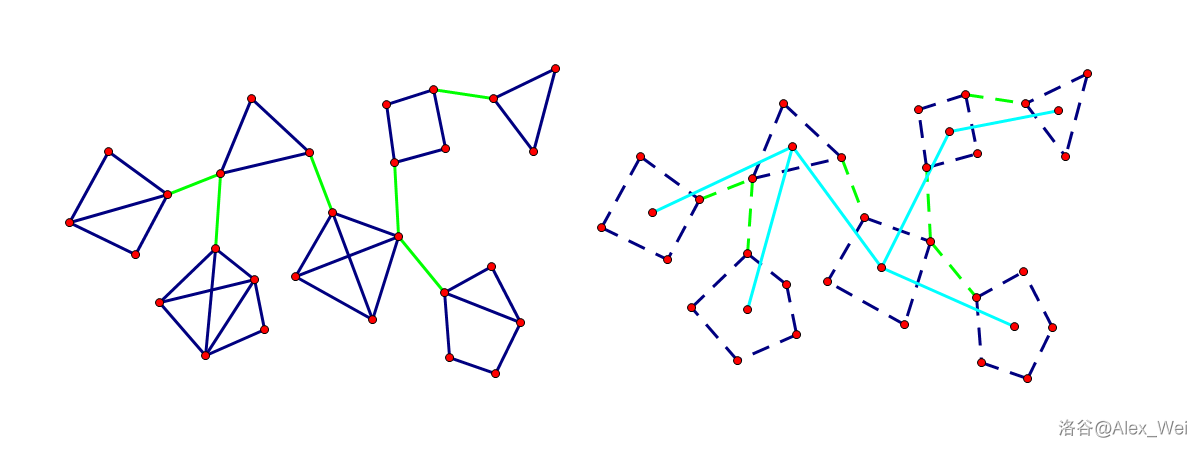
缩点后每个边双是一个点，每个桥是一条边，形成一棵树。树上两点间的距离就是原图中两点间桥的个数。