信息论领域内得计算方法仿真，Entropy。计算熵

目标：

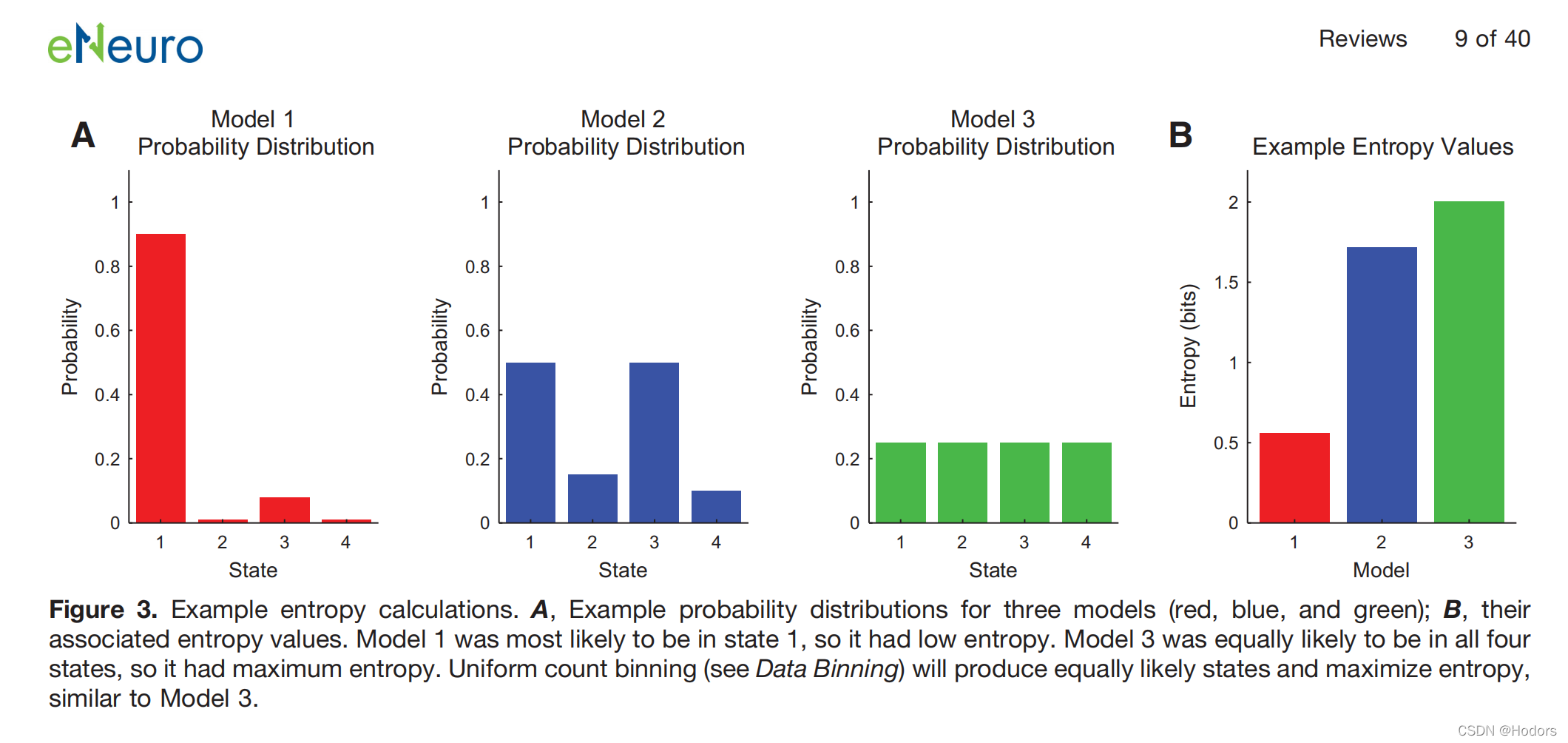
我的code 

#### Figure 2 两种生成概率直方图的方法；

#生成长度为100，值从3到15的随机数序列；
import numpy as np
np.random.seed(2)

data = np.random.randint(low=3, high=15, size=100, dtype=np.uint8)

minv = min(data)
maxv = max(data)
numb = 4

delt = (maxv - minv)//numb
stat1 = [minv, minv+delt*1]
stat2 = [minv+delt*1, minv+delt*2]
stat3 = [minv+delt*2, minv+delt*3]
stat4 = [minv+delt*3, maxv]

count = [0, 0, 0, 0]
for va in data:
    if stat1[0] <= va <= stat1[1]:
        count[0] += 1
    elif stat2[0] <= va <= stat2[1]:
        count[1] += 1
    elif stat3[0] <= va <= stat3[1]:
        count[2] += 1
    elif stat4[0] <= va <= stat4[1]:
        count[3] += 1
    else:
        print("no")

print(count)

#绘制直方图
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
x = [1, 2, 3, 4]
y = count
ax.bar(x, y, width=1, edgecolor="white", linewidth=0.7)
plt.show()

#计算熵
p1 = count[0] / len(data)
p2 = count[1] / len(data)
p3 = count[2] / len(data)
p4 = count[3] / len(data)

Hdata = p1 * np.log2(1/(p1))+p2 * np.log2(1/(p2))+p3 * np.log2(1/(p3))+p4 * np.log2(1/(p4))
print(u"The entropy of variable data is H(x) = {:.2f} bits".format(Hdata))

#再来一个等概率的图

#绘制直方图
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
x = [1, 2, 3, 4]
y = [25, 25, 25, 25]
ax.bar(x, y, width=1, edgecolor="white", linewidth=0.7)
ax.set_ylim(0, 50)
plt.show()
#计算熵
p1 = 0.25
p2 = 0.25
p3 = 0.25
p4 = 0.25

Hdata = p1 * np.log2(1/(p1))+p2 * np.log2(1/(p2))+p3 * np.log2(1/(p3))+p4 * np.log2(1/(p4))
print(u"The entropy of variable data is H(x) = {:.2f} bits".format(Hdata))

结果：

1、

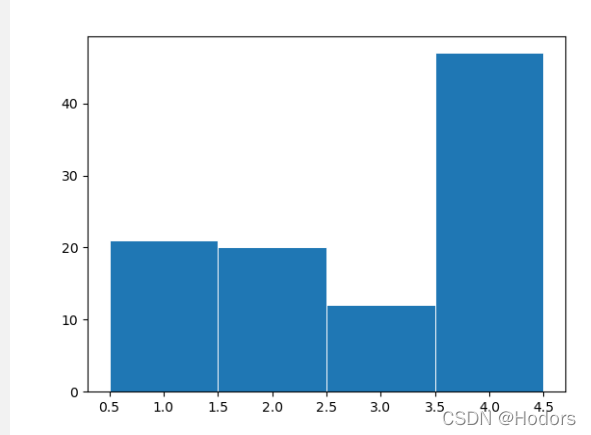
2、

The entropy of variable data is H(x) = 1.82 bits

3、再来一个等概率的图；

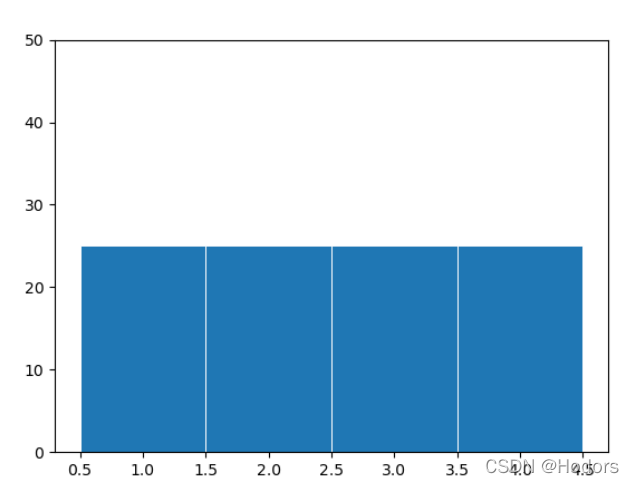
3、

 The entropy of variable data is H(x) = 2.00 bits

所以，等概率，就是2.0bit

什么含义呢？要确定变量data的值，至少得问两次“是否”问题。