博客作业06--图
1.学习总结
1.1图的思维导图
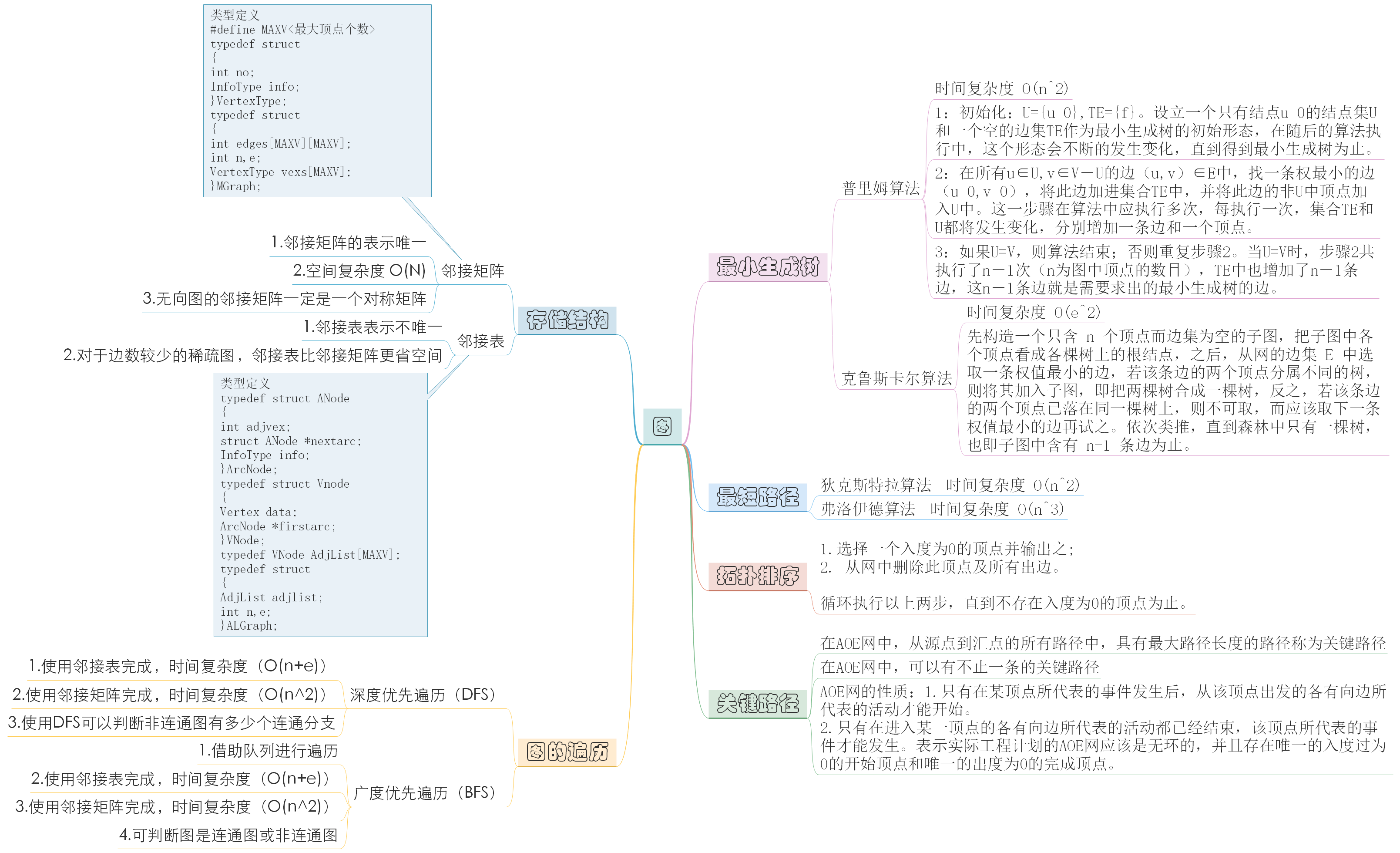
1.2 图结构学习体会
- 深度优先遍历与广度优先遍历算法应该说是图中最基本的两个算法,许多算法都带有深度遍历与广度遍历的影子,所以是必须掌握的。
- 克鲁斯卡尔算法是比普里姆算法更为精确的算法,但对于规模较大的最小生成树问题,求解速度较慢,所以稀疏图用克鲁斯卡尔算法,而稠密图用普里姆算法求解。
- 在最小生成树中从一个顶点到另一顶点的路径不一定是最短的,但在狄克斯特拉树中从根结点到每个叶子结点的路径都是最短的。
- 只有有向无环图才可以进行拓扑排序,所以拓扑排序可以用来判断图中是否存在环。
2.PTA实验作业
2.1.1 题目1:图着色问题
2.1.2 设计思路
int main()
{
CreateMGraph();//建图
for i=0 to N
flag=1;colornum=0;//颜色数量
for j=0 to n
输入颜色;颜色数组存储颜色
int Flag=0;
for k=0 to k<j
if 颜色数组中存在与当前颜色相同的,则判断错误,即Flag=1
if 颜色正确
颜色数量加一
if 颜色数量不为K,判断为错误,即flag=0
if 颜色数量正确
for j=0 to n
for k=0 to n
judge(j);//进入函数判断配色方案是否正确
if flag==0
break;//停止循环
if flag==1 输出 Yes
else 输出 No
}
void judge(int p)
{
if p遍历过 或 此时flag为0,则不再进行任何操作
else
标记p遍历过
for i=0 to n
if p与i有关联,即edges[p][i]==1
if p处颜色与i处颜色相同
flag=0 并且停止循环
else if i未遍历过
i进入函数judge进行递归
}
2.1.3 代码截图
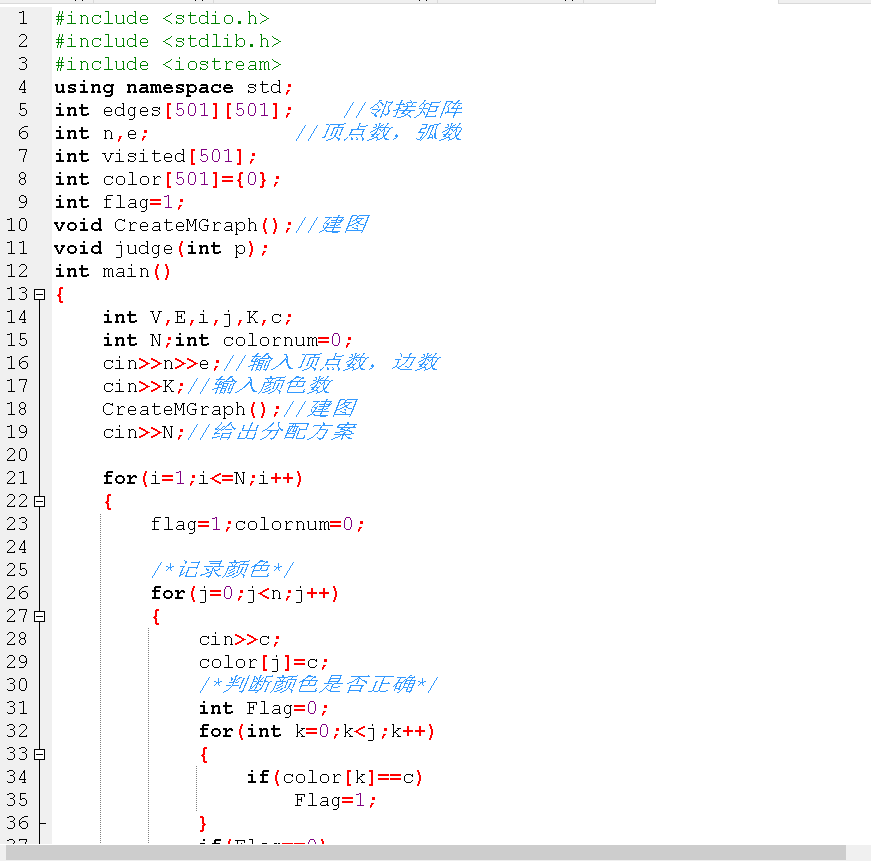
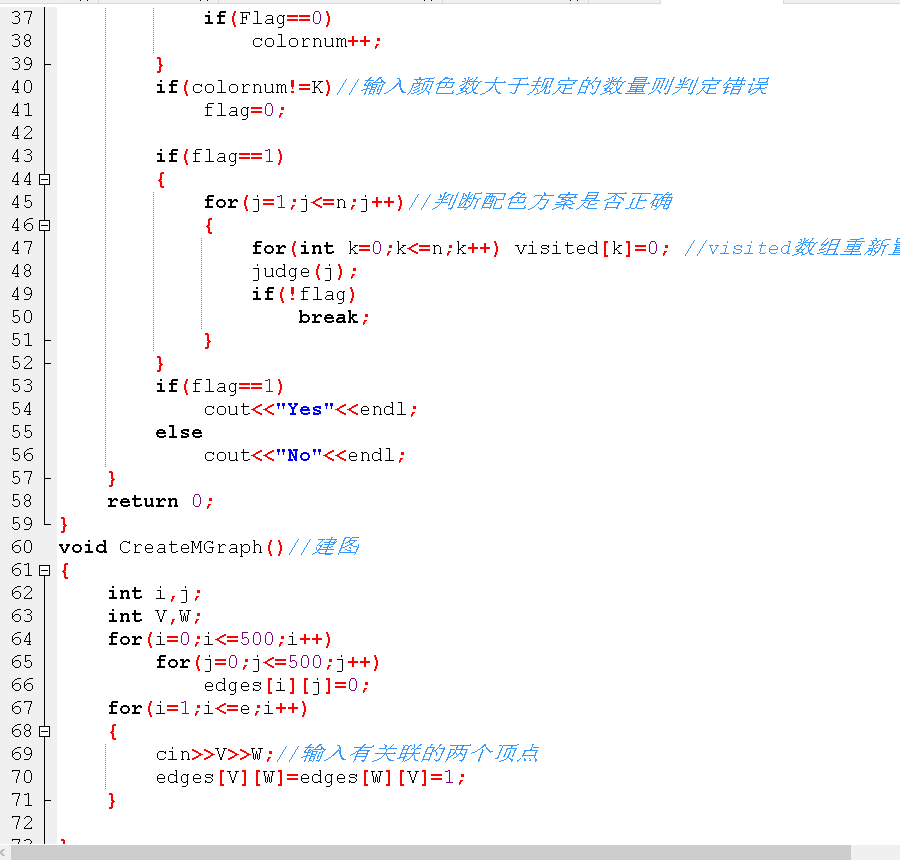

2.1.4 PTA提交列表说明
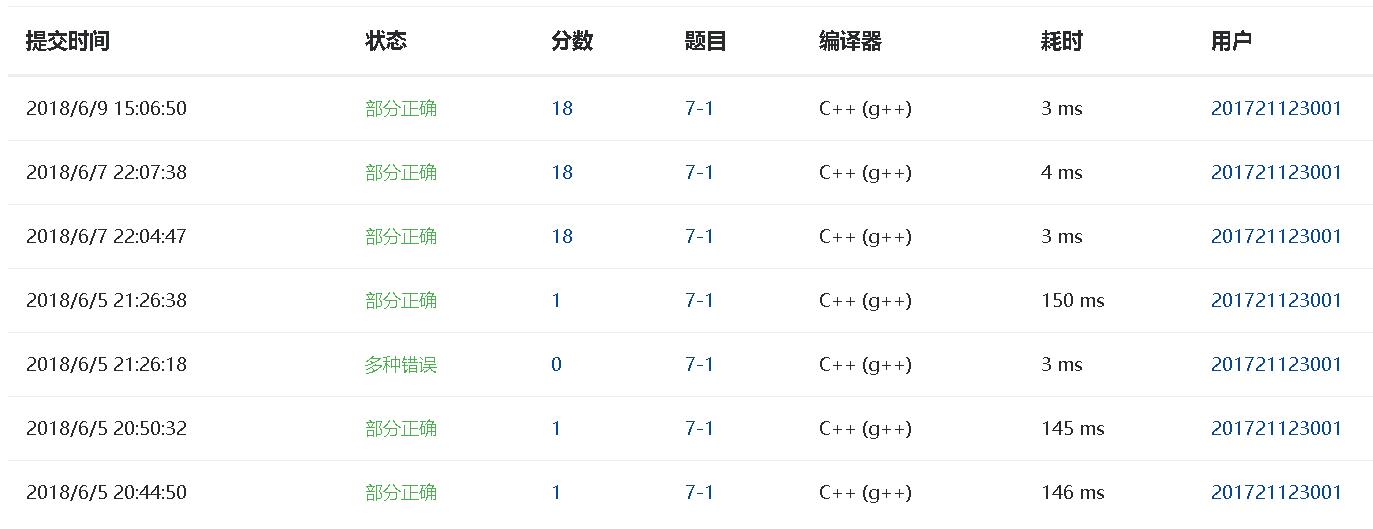
- 1.结构体中无法定义过大的数组
- 2.缺少判断颜色数量是否正确的操作
- 3.忘记将visited数组重置为0
- 4.还有错误存在,但目前未找出来
2.2.1 题目2:公路村村通
2.2.2 设计思路
/*由普里姆算法改造*/
int prime(int n)
{
cost[1]=0; //初始化
for i=2 to n
cost[i]=road[1][i];
for i=1 to n
min初始为一个极大值
for j=1 to n
if 通往j的费用不为0 且 小于 min
min=cost[j];k=j;
if k!= 0
num=cost[k]+num;//记录最小费用
cost[k]=0; // 作为记录过的标志
for j=1 to n
if j未访问过 且 k到j的费用小于当前j的费用
cost[j]=coad[k][j];
else
输出 -1;flag=1;退出结束循环
if flag==0
输出最低成本
}
2.2.3 代码截图


2.2.4 PTA提交列表说明
第一次提交时只有第一个测试点对,调试的时候发现当k==0时即表示找不到最小路径,此时就可以停止循环退出,多考虑反而会导致结果错误,但是仍有一个测试点不对,最后的通过是在完成7-7 即旅游规划那道题后面,尝试着也在数组初始化的时候做修改,于是通过了。

2.3.1 题目3:旅游规划
2.3.2 设计思路
/*该道题主要运用狄克斯特拉算法*/
void Dijkstra(int n,int c1,int c2)
{
for i=0 to n //初始化
cost[i]=fare[c1][i];
dist[i]=city[c1][i];
visited[c1]=1;dist[c1]=0;
for i=0 to n //找出距离c1最小的点
mindis初始化为最大数值
for j=0 to n
if j点未访问过 且 j到c1的距离小于mindis
k=j;
mindis=dist[j];//更新最小距离
for j=0 to n //修改未访问过顶点的距离
if j未访问过
if k到j的距离加上此时最小距离小于j到c1的距离,改变j的数值
dist[j]=dist[k]+city[k][j];
cost[j]=cost[k]+fare[k][j];
else if 距离相同 且 所用费用小于此时总费用
cost[j]=cost[k]+fare[k][j];
}
2.3.3 代码截图


2.3.4 PTA提交列表说明
之前提交的时候只有第一个测试点是对的,上课的时候听同学讲矩阵中对角线初始为0,其余设为最大值,考虑到本题要求不大于500,INF就设为501,但是提交后发现当N,M为最大值时段错误,将初始数组的范围由M改成501,就对了。

3.截图本周题目集的PTA最后排名
本次题目集总分:310分
3.1 PTA排名
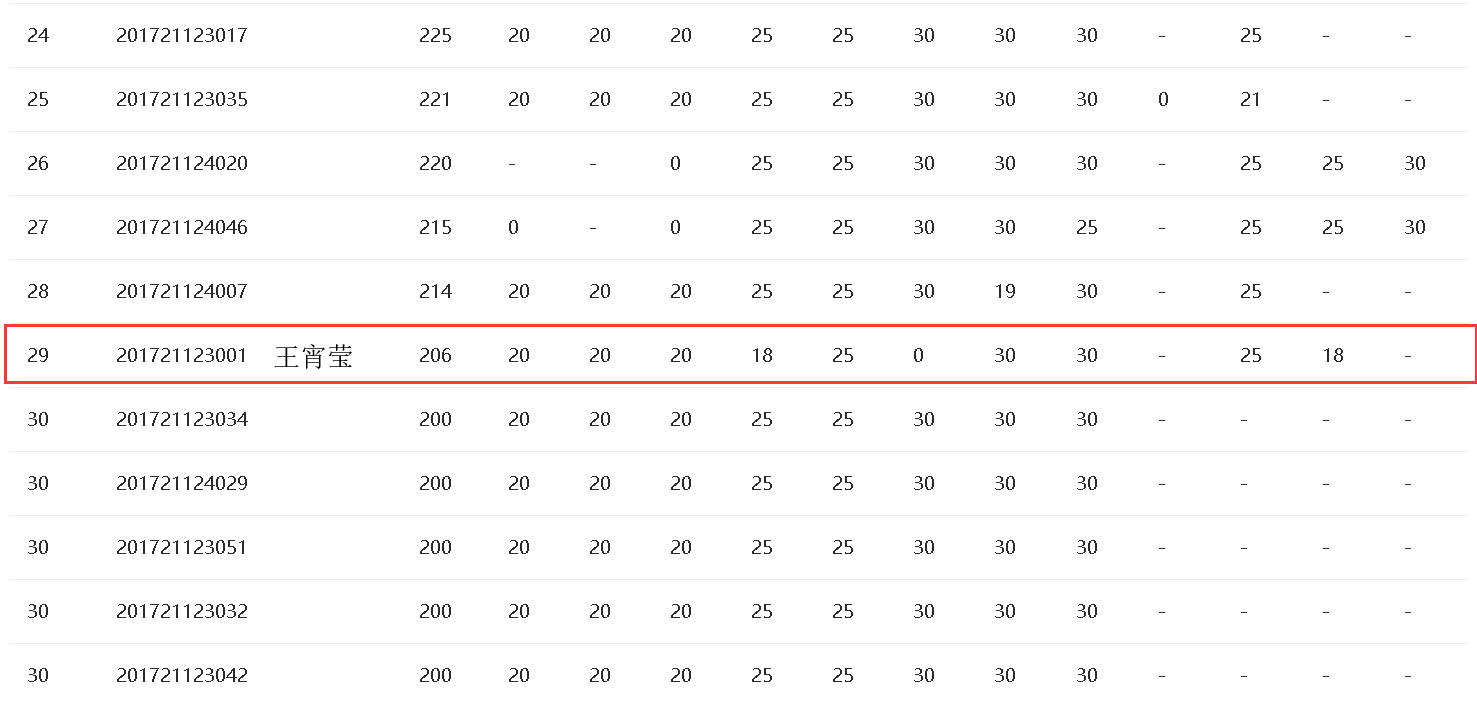
3.2 我的总分:206
4. 阅读代码
利用图完成数独
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long
typedef pair<int,int>pii;
const int N = 20;
const int mod = 765431;
int n=9;
char mp[N][N]; // 原图
char opt[N][N]; // 中间图
bool vol[N][N],row[N][N]; //row[i][j] 第i行中已经有j数字,vol[i][j]第i列中已经有j数字
pii P[100];int sz; // 存储所有的未知位置
int flag;
bool check(int now,int val){ // 查询 3*3宫
pii p = P[now];
int n=(p.first-1)/3*3;
int m=(p.second-1)/3*3;
for(int i=n+1;i<=n+3;i++){
for(int j=m+1;j<=m+3;j++){
if(opt[i][j] == val+'0') return false;
}
}
return true;
}
void dfs(int now){
if(flag) return ;
if(now==sz) {
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) {
if(j!=1) putchar(' ');
printf("%c",opt[i][j]);
}
puts("") ;
}
flag=1;
return ;
}
pii p = P[now];
for(int j=1;j<=9;j++){
if( !row[p.first][j] && !vol[p.second][j] && check(now,j)){
row[p.first][j]=1; vol[p.second][j]=1;
opt[p.first][p.second]=j+'0';
dfs(now+1);
row[p.first][j]=0; vol[p.second][j]=0;
opt[p.first][p.second]=mp[p.first][p.second];
}
}
}
int main(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%c",&mp[i][j]);
opt[i][j]=mp[i][j];
if(mp[i][j] == '*') {
P[sz].first=i;
P[sz++].second=j;
}else {
int val=mp[i][j]-'0';
vol[j][val]=1;
row[i][val]=1;
}
}
getchar();
}
flag=0;
dfs(0);
return 0 ;
}
前不久在玩数独,碰巧看到了用图来解决数独问题,觉得很有意思。
数独游戏要求九宫格中每一行每一列不能有重复的数字出现,那么就意味着这个程序需要不断进行比较判断,不能出现重复的数字。首先利用深度遍历往宫格里填数字,然后检查在该数字所处的行列是否有出现过,再在3*3的宫格里判断是否有相同的数字,若最后结果都不行则需要改变宫格中的数字,再次判断。
测试结果:
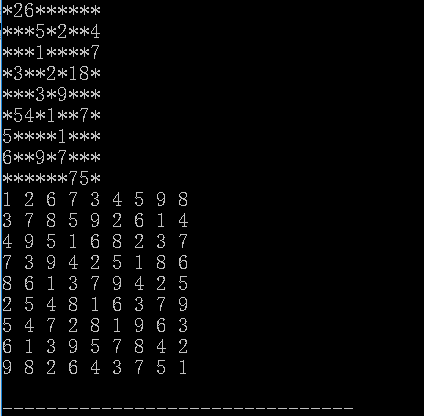
博客指路→(https://blog.csdn.net/qq_37383726/article/details/79703157)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号