栈
栈 Stack
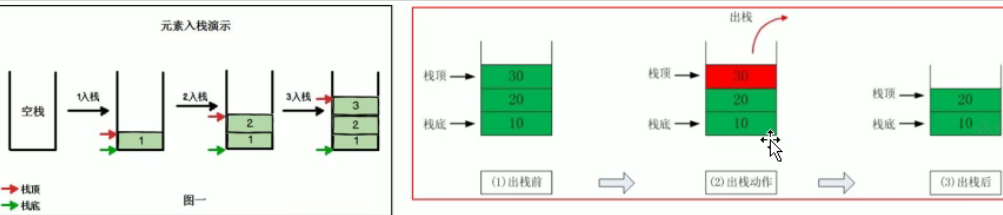
- 先入后出
- 栈顶Top (变化的一端),栈底Bottom(固定的一端)
- pop push isEmpty
- 应用场景:
子程序调用,处理递归调用,表达式的转换,二叉树的遍历,图的深度优先搜索
1. 数组模拟栈
class myArrayStack{
private int maxSize;
private int[] stack;
private int top=-1; //栈顶,初始值为-1
//构造器
public myArrayStack(int maxSize){
this.maxSize = maxSize;
stack = new int[maxSize];
}
public boolean isFull(){
return top==maxSize-1;
}
public boolean isEmpty(){
return top==-1;
}
public void push(int value){
if (isFull()){
System.out.println("栈满,无法入栈~");
return;
}
top++;
stack[top] = value;
}
public int pop(){
if (isEmpty()){
throw new RuntimeException("栈空,无法出栈~");
}
return stack[top--];
}
public void list(){
if (isEmpty()){
System.out.println("栈为空,无法遍历~~");
}
//从栈顶开始遍历
for (int i = top; i >=0; i--) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
}
2. 单向链表模拟栈(头插法)
class LinkedListStack{
//初始化头节点
private Node head = new Node(-1);
public boolean isEmpty(){
return head.next==null;
}
//头插法 模拟 入栈
public void push(Node node){
Node top = head.next; //第一个节点
node.next = top;
head.next = node;
}
//出栈
public Node pop(){
if (isEmpty()){
throw new RuntimeException("栈空,无法出栈~");
}
Node top = head.next;
head.next = top.next;
return top;
}
//遍历
public void list(){
if (isEmpty()){
System.out.println("栈空,无法遍历~");
return; //停止函数
}
Node top = head.next;
int i=0;
while (top!=null){
System.out.printf("stack[%d]=%d\n",i,top.value);//stack[i]为逆序
i++;
top = top.next;
}
}
}
栈实现计算器
单个数字之间的 加减乘除: "3+2*6-2"
-
索引index 遍历表达式
-
创建数栈 numStack,符号栈 operStack(分别存数字num 与操作符oper )
-
符号栈:
-
运算符优先级
oper <= operStack[top]:numStack.pop 两个数 + operStack.pop一个符号进行运算 【b x a】
numStack.push运算结果,operStack.push 操作符
-
符号栈为空,操作符优先级 oper > operStack[top],直接入栈
-
-
表达式扫描完毕后,pop 数栈与符号栈 进行运算
-
直到 数栈只有一个数字时,得到表达式结果
前,中,后缀表达式
(扫描到 运算符 就pop出两个数字进行运算,只需要一个栈【用来存数字】)
- 前缀表达式:
- 从右至左扫描表达式, 栈顶 * 次顶 (*为运算符)
- 【- X + 3 4 5 6】 ---> (3+4) X 5 - 6
- 中缀表达式:
- 常见的运算表达式
- 后缀表达式:(逆波兰表达式)
- 从左至右扫描, 次顶 * 栈顶
- 【3 4 + 5 X 6 -】---> (3+4) X 5 - 6
逆波兰计算器
- 题目:
(3+4)x5-6 => [ 3 4 + 5 x 6 - ] 先中缀转后缀
输入后缀表达式(逆波兰表达式),使用栈 计算其结果 29
支持 括号和多位整数
表达式输入用 空格隔开 - 思路:
- 先把表达式的值 放到数组里面
- 遍历数组,压入栈
- 数字:直接入栈
- 运算符:pop 次顶元素 * 栈顶元素 (*代表运算符)
逆波兰计算器 代码实现
public class PolandNotation {
public static void main(String[] args) {
String suffixExpression = "3 4 + 5 x 6 -";
List list = getListString(suffixExpression);
int res = calculate(list);
System.out.printf("逆波兰表达式:%s = %d",suffixExpression,res);
}
//1.创建数组 存表达式
public static List getListString(String expression){
List<String> list = new ArrayList<>();
String[] listString = expression.split(" ");
for (String s : listString) {
list.add(s);
}
return list;
}
//2.遍历数组 入栈 进行计算
public static int calculate(List<String> list){
Stack<String> stack = new Stack<>();//创建栈
for (String s : list) {
if (s.matches("\\d+")){ //匹配多个数字
stack.push(s);
}else{ //遇到运算符时,进行运算 次顶*栈顶
int num1 = Integer.parseInt(stack.pop()); //栈顶
int num2 = Integer.parseInt(stack.pop()); //次顶 (字符串转int)
int res = 0;
if (s.equals("+")){
res = num2 + num1;
}else if (s.equals("-")){
res = num2 - num1;
}else if (s.equals("x")){
res = num2 * num1;
}else if (s.equals("/")){
res = num2 / num1;
}else {
throw new RuntimeException("运算符有误");
}
stack.push(""+res); //结果入栈 (int转字符串)
}
}
return Integer.parseInt(stack.pop()); //弹出最后一个数(即结果)
}
}
中缀转后缀表达式
- 初始化两个栈:运算符栈s1 和 存储中间结构的栈s2
- 从左到右 扫描中缀表达式
- 遇到数字:压入s2
- 遇到运算符:
- s1为空 或 栈顶为左括号( 或 优先级高于栈顶运算符:压入s1;
- 否则将 s1的栈顶pop 放到s2中,继续比较。
- 遇到括号:
- 左括号( ,直接压入s1;
- 右括号) ,不断pop s1放到s2 直到遇到左括号,将这对括号丢弃。
- 扫描完毕后,将s1剩余的元素 pop到s2中
- 依次弹出s2的元素,结果的逆序即为 后缀表达式。
( 栈s2没有pop操纵,故可以将s2用数组代替,就不用再逆序)
中缀转后缀表达式 代码实现
//中缀 转后缀
public static List toSuffixExpression(List<String> ls){
//1.初始化两个栈
Stack<String> s1 = new Stack<>(); //运算符栈
List<String> s2 = new ArrayList<>(); //存放中间结果 list替代stack
//2.遍历中缀表达式
for (String item : ls) {
if (item.matches("\\d+")){ //a匹配到数字
s2.add(item);
}else if (item.equals("(")){ //b匹配到左括号
s1.push(item);
}else if (item.equals(")")){ //c匹配到右括号
while (! s1.peek().equals("(")){ //s1栈顶不是 ( 时 !!!!!
s2.add(s1.pop()); //在匹配到左括号前 不断把pop(s1) 放到s2中
//System.out.println("s2: "+s2.toString());
}
s1.pop(); //并消除这对括号
}else { //d匹配到运算符
//d2 否则,s1的元素pop到s2中,并继续匹配
while(s1.size() !=0 && priority(item) <= priority(s1.peek())){
s2.add(s1.pop());
}
//d1 匹配到 栈顶为空 或 运算符优先级 大于栈顶运算符
s1.push(item); //直接入栈
}
}
//3. 扫描完后,将s1剩余元素pop到s2中
while (s1.size() != 0){
s2.add(s1.pop());
}
//4. s2剩下的元素弹出 结果的逆序就是后缀表达式 --> s2转用数组,直接遍历就是结果
return s2;
}
//字符串转数组
public static List getInfixList(String str){
//先把字符串转为数组
List<String> list = new ArrayList<>();
int i = 0; //记录位置
String num; //拼接多位数
char ch; //代表每一位字符
do {
ch = str.charAt(i); //获取第i个字符
if (ch <48 || ch>57){ //为运算符的情况
list.add(""+ch); //字符转字符串
i++;
}else { //为数字的情况
num="";
while (i < str.length() && str.charAt(i)>=48 &&str.charAt(i)<=57){ //ascll码 48-57代表数字0-10
num+=str.charAt(i);
i++; //字符后移
}
list.add(num);
}
}while (i < str.length());
return list;
}
//获取运算符优先级
public static int priority(String oper){
if (oper.equals("+") || oper.equals("-")){
return 1;
}else if (oper.equals("x") || oper.equals("/")){
return 2;
}else
return 0;
}
我是菜鸡啊


 浙公网安备 33010602011771号
浙公网安备 33010602011771号