题解:P14026 [ICPC 2024 Nanjing R] 我将如潮水般归来
洛谷题目传送门:P14026 [ICPC 2024 Nanjing R] 我将如潮水般归来
在博客园阅读效果更佳:https://www.cnblogs.com/wwwidk1234/p/19107414
作为一个那维莱特厨看到这个题目名啪的一下就点进来了啊,然后被硬控了 9.5 个小时,从中午 12:00 一直搞到了 19:30 才调完。
这道题需要用到的妙妙工具是:任意角三角函数、向量(是的没错就这么多,不需要复数微积分等等一些奇怪的东西)
题目大意
那维莱特是一只可爱的小海獭,他初始时站在原点 \(O(0,0)\) 并面向方向 \((x_0,y_0)\),进行 \(t\) 秒的「重击·衡平推裁」,并以 \(\omega=1 \operatorname{rad/s}\) 的恒定的角速度转圈。
一个点能被攻击到,当且仅当这个点与从 \(O\) 指向那维莱特方向的射线(攻击射线 \(l\))的距离 \(\le d\),其中 \(d\) 为喷水范围。如果一个魔物(\(n\) 个点的凸多边形)被攻击到(即与攻击范围的交集不为空),那么每秒将会受到 \(1\) 点伤害。求 \(t\) 秒内那维莱特打出的伤害。
题目解析
那维莱特转圈显然是有周期性的:每秒转 \(1 \operatorname{rad}\),转一圈就是 \(2\pi \operatorname{rad}\),于是只需要把题目中所有的角度都化成 \(\theta \in [0,2\pi)\) 就可以了。
看到数据范围 \(t \le 10^4\),每 \(1\) 秒钟就要调整一下那维莱特的角度然后计算有没有交集,这样时间复杂度就爆炸了。这时想到一个 trick:只考虑“端点”部分(该 trick 应用比较广泛,一个例子是 NOIP2023 T4 天天爱打卡)。
对于这道题,我们需要考虑的“端点”为那维莱特是否能打到怪物的临界角度,如果上 \(1 \operatorname{rad}\) 那维莱特能打到,这 \(1 \operatorname{rad}\) 打不到了;或者上 \(1 \operatorname{rad}\) 打得到,但是这 \(1 \operatorname{rad}\) 打不到了,这就是临界角度。
【思考 1】
什么角度可能出现那维莱特是否能攻击到怪物的状态发生改变?
显然地,要么那维莱特的攻击范围刚刚接触到怪物的某个点,要么刚刚离开某个点。如下图所示:

怎么求出这两个角度?
对于多边形的第 \(i\) 个点 \(P(x,y)\),记:
- 其到原点距离为 \(r=\sqrt{x^2+y^2}\),用幼儿园学过的勾股定理推导即可;
- 其方位角(即 \(OP\) 与 \(x\) 轴的夹角)为 \(\theta\)(可用
C++ atan2函数求出) - 其角度偏差(射线 \(OP\) 与攻击射线 \(l\) 的夹角)为 \(\Delta=\arcsin \dfrac{d}{r}\)(\(d\) 为喷水范围)这个 \(\arcsin\) 怎么来的?请看下面这张图:
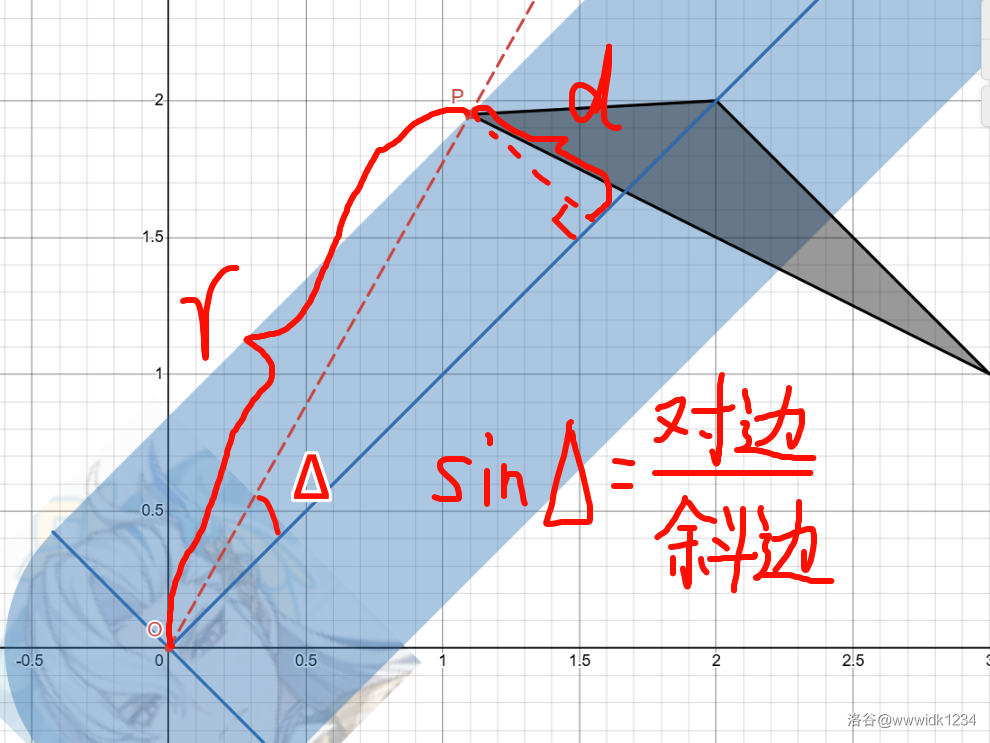
然后我们就可以求出这个点的临界角度:\(\theta \pm \Delta\)。
注:atan2 函数的值域为 \((-\pi,2\pi]\),我们要把这个角度转换成 \([0,2\pi)\) 内的一个角。
将这些临界角度去重排序之后,可以得到若干个需要考虑的角度区间 \([l_i,r_i]\),只需要在这些区间上判断怪物有没有被打到,然后就可以算每一个区间的贡献了。
对于每一个角度区间 \([l_i,r_i]\),我们不妨直接在区间里面随便选择一个角度 \(\theta=\dfrac{l_i+r_i}{2}\) 检查有没有被那维莱特击中(因为这一个区间里面被击中的状态一直都是不变的)然后就可以算贡献了。
注意:为了方便第一个和最后一个角的区间的贡献计算,我们要把 \(0\) 和 \(2\pi\) 加进临界角度里面。
【思考 2】
如何判断当那维莱特旋转到 \(\theta\) 时,能不能打到怪物?
直接判断攻击区域与多边形是否有交集会很麻烦,所以我们只需要考虑多边形的点和边有没有被击中就好了。
考虑以那维莱特为原点,攻击射线(由 \(x\) 轴正方向逆时针旋转 \(\theta\) 得到的射线)方向为 \(u\) 轴正方向,垂直于攻击射线方向为 \(v\) 轴正方向,建立平面直角坐标系 \(uOv\)。对于原平面直角坐标系的一个点 \(P(x,y)\),这个点在 \(u\) 轴上的投影为 \(x \cos \theta+y \sin \theta\),在 \(v\) 轴上的投影为 \(-x\sin \theta+y\cos \theta\),推导过程如下:
新坐标系 \(u\) 轴的单位基向量 \(\boldsymbol{e}_u\),在原坐标系 \(xOy\) 中坐标为 \((\cos \theta,\sin \theta)\)(因为 \(u\) 轴是由 \(x\) 轴逆时针旋转 \(\theta\) 过来的)
新坐标系 \(v\) 轴的单位基向量 \(\boldsymbol{e}_v\),在原坐标系 \(xOy\) 中坐标为 \((\cos (\theta+\dfrac \pi 2),\sin(\theta + \dfrac{\pi}{2}))\),由三角函数诱导公式得坐标为 \((-\sin \theta,\cos \theta)\)。
因为点 \(P(x,y)\) 的位置向量 \(\overrightarrow{OP}\) 是固定的,所以:
- 在原坐标系 \(xOy\) 中,\(\overrightarrow{OP} = x\cdot\boldsymbol{i} + y\cdot\boldsymbol{j}\)(\(\boldsymbol{i},\boldsymbol{j}\) 为原 \(x,y\) 轴单位基向量);
- 在新坐标系 \(uOv\) 中,\(\overrightarrow{OP} = u\cdot\boldsymbol{e}_u + v\cdot\boldsymbol{e}_v\)(\(u,v\) 即为点 \(P\) 在 \(u,v\) 轴上的投影,也就是新坐标)。
由于位置向量本身不变,将 \(\boldsymbol{e}_u, \boldsymbol{e}_v\) 的原坐标代入,得:
\[x\boldsymbol{i} + y\boldsymbol{j} = u(\cos\theta\boldsymbol{i} + \sin\theta\boldsymbol{j}) + v(-\sin\theta\boldsymbol{i} + \cos\theta\boldsymbol{j}) \]由等式两侧 \(\boldsymbol{i}\) 和 \(\boldsymbol{j}\) 的系数分别对应相等,得:
- \(\boldsymbol{i}\) 的系数:\(x = u\cos\theta - v\sin\theta\)
- \(\boldsymbol{j}\) 的系数:\(y = u\sin\theta + v\cos\theta\)
求 \(u\)(\(P\) 在 \(u\) 轴上的投影):将第一个方程乘 \(\cos\theta\),第二个方程乘 \(\sin\theta\),两式相加:\(x\cos\theta + y\sin\theta = u(\cos^2\theta + \sin^2\theta) = u\),得:
\[{u = x\cos\theta + y\sin\theta} \]求 \(v\)(\(P\) 在 \(v\) 轴上的投影):将第一个方程乘 \(\sin\theta\),第二个方程乘 \(\cos\theta\),两式相减(第二个减第一个):\(y\cos\theta - x\sin\theta = v(\cos^2\theta + \sin^2\theta) = v\),得:
\[{v = -x\sin\theta + y\cos\theta} \]推导完毕。
(注:如果你不了解投影,可以简单地理解为:平面直角坐标系 \(xOy\) 内一点 \(P(x,y)\),在平面直角坐标系 \(uOv\) 的投影就是这个点在 \(uOv\) 内的坐标 \(P(u,v)\))。
对于多边形上的一个点 \(P(x,y)\),判断这个点在不在攻击范围内,首先将点投影到坐标系 \(uOv\) 中,然后判断分别 \(u,v\) 轴上的投影 \(u_P,v_P\) 是否同时满足以下两个条件:
- \(P\) 在 \(u\) 轴正方向或原点:即 \(u=x \cos \theta+y \sin \theta \ge 0\);(因为攻击是一个射线)
- \(P\) 到 \(v\) 轴距离不超过 \(d\):即 \(v=\left|-x\sin\theta + y\cos\theta\right| \le d\)。(因为攻击范围只有 \(d\))
这样攻击范围 \(G\) 就可用以下集合表示:(忽略在 \((0,0)\) 处半径为 \(d\) 的一个圆,因为题目保证这个圆与多边形没有公共点)
(注:\((u,v)\) 的意义是在坐标系 \(uOv\) 下某一点的坐标)
对于多边形的一条边 \(PQ,P(x_p,y_p),Q(x_q,y_q)\),要根据求出投影 \(P(u_p,v_p),Q(u_q,v_q)\)(求投影的方法同上),线段 \(PQ\) 也可以用集合 \(L\) 表示(其中 \(t \in [0,1]\) 对应线段上所有点):
其中:\(\Delta u = u_q - u_p,\Delta v = v_q - v_p\)。
怪物能被那维莱特打到,当且仅当 \(L,G\) 两图形有交集,即 \(L \cap G \ne \varnothing\)。我们可以将条件 \(u \ge 0 \land \left|v\right|\le d\) 拆开两部分,先根据 \(u \ge 0\) 求出 \(t\) 的范围 \(T\),然后再看一下 \(v\) 轴是否在范围内即可。
首先先解 \(u \ge 0,t\) 的取值范围 \(T\):
-
若 \(\Delta u =0,u_q=u_p\),则线段在 \(u\) 轴上的投影就变成了一个点,如果这个点满足 \(u \ge\) 那么整条线段都可以取值,即 \(T=[0,1]\),否则 \(T=\varnothing\);
-
若 \(\Delta u > 0,u_q>u_p\),则由 \(u = u_p + t\Delta u>0\) 知 \(t \ge -\dfrac{u_p}{\Delta u}\),故 \(T=[-\dfrac{u_p}{\Delta u},1]\);
-
若 \(\Delta u<0,u_q<u_p\),同上可知 \(T=[0,-\dfrac{u_p}{\Delta u}]\)。
然后在根据 \(T\) 的上下界求出两个端点值,再看这两个端点是否满足 \(\left|v\right| \le d\) 即可。
【思考 3】
如何计算思考 1 中角度区间 \([l_i,r_i]\) 对伤害的贡献?
判断能不能击中,如果能:
首先要求出这个角度区间在哪些旋转周期会有:显然应该满足“不早于攻击开始且不晚于攻击结束”,又已知那维莱特旋转的角速度 \(\omega=1 \operatorname{rad/s}\),所以应该周期数 \(T\) 的取值范围应该是:
其中 \(\theta_0\) 为那维莱特初始时面对的方向角度。
对于每一个整数 \(T \in \left[ \left\lceil\dfrac{\theta_0-r_i}{2\pi} \right\rceil,\left\lfloor \dfrac{t+\theta_0-l_i}{2\pi} \right\rfloor \right]\),计算出在这个周期时的角度区间 \([L=l_i-\theta_0+2\pi T,R=r_0-\theta_0+2\pi T]\),然后得出那维莱特通过这一角度区间所需要的时间 \(R-L\) 即为这一段区间的伤害。
然后,我们终于 AC 了此题!
参考程序
注:由于代码中涉及到的变量比较多,为了方便调试和阅读,故使用了中文变量名。在 C++23 中,支持中文变量名。
本篇题解图像使用 desmos 绘制,该图像工程文件地址:https://www.desmos.com/calculator/ydtirahvmn
AC 记录:https://www.luogu.com.cn/record/236684113
//I Love Neuvillette FOREVER
#include<bits/stdc++.h>
#define y0 Neuvillette_is_a_lovely_sea_otter //防止 CE 没别的意思
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=107;
constexpr double pi=3.1415926535897932384626433832;
constexpr double eps=1e-9;
constexpr double 保留多少位小数=12;
struct point{double x,y;};
int n,周期数;
double x0,y0,喷水范围,喷水时间,初始角;
point poly[N];
inline double change(double k) //把任意角k转化到[0,2π)区间里面
{
if(0<=k&&k<2*pi) return k;
while(k<0) k+=2*pi;
while(k>=2*pi&&k>=0) k-=2*pi;
return k;
}
template<typename T>
inline vector<T> unique(vector<T> a) //a数组去重
{
sort(a.begin(),a.end());
vector<T> res;
for(int i=0;i<(int)a.size();i++)
if(i==0||a[i]-a[i-1]>eps) res.push_back(a[i]);
return res;
}
//检查攻击方向为θ时能不能打到怪物
inline bool check(double θ)
{
const double sinθ=sin(θ);
const double cosθ=cos(θ);
for(int i=1;i<=n;i++) //顶点在不在喷水范围内
{
double u轴投影=poly[i].x*cosθ+poly[i].y*sinθ;
double v轴投影=poly[i].x*(-sinθ)+poly[i].y*cosθ;
if(u轴投影>=-eps&&abs(v轴投影)<=喷水范围+eps) return 1; //能打到
}
for(int P=1;P<=n;P++) //线段在不在喷水范围内
{
int Q=(P+1>n)?1:(P+1); //找线段的另外一个端点
double Pu轴投影=poly[P].x*cosθ+poly[P].y*sinθ;
double Pv轴投影=poly[P].x*(-sinθ)+poly[P].y*cosθ;
double Qu轴投影=poly[Q].x*cosθ+poly[Q].y*sinθ;
double Qv轴投影=poly[Q].x*(-sinθ)+poly[Q].y*cosθ;
double du=Qu轴投影-Pu轴投影;
double dv=Qv轴投影-Pv轴投影;
double seg_l=-12180211,seg_r=-12180211; //区间s=[l,r]表示在u轴正方向的部分
//l=0:线段左端点P在u轴正方向;l=1:线段右端点Q在u轴正方向
if(abs(du)<=eps) //PQ垂直于攻击方向
{
if(Pu轴投影>=-eps) seg_l=0,seg_r=1; //一整条线段都在正方向
else continue;
}
else if(du>eps)
{
seg_l=(0-Pu轴投影)/du;
seg_r=1;
if(seg_l<0) seg_l=0;
if(seg_l>seg_r) continue; //空区间
}
else if(du<eps)
{
seg_l=0;
seg_r=(0-Pu轴投影)/du;
if(seg_r>1) seg_r=1;
if(seg_l>seg_r) continue; //空区间
}
else cerr<<"那维莱獭不知道哦\n";
if(seg_l<-10000) cerr<<"那维莱獭不知道哦(seg_l)\n";
if(seg_r<-10000) cerr<<"那维莱獭不知道哦(seg_r)\n";
//对于seg_l,seg_r分别求出两个投影
double segl处的v轴投影=Pv轴投影+seg_l*dv;
double segr处的v轴投影=Pv轴投影+seg_r*dv;
if(segl处的v轴投影>segr处的v轴投影)
swap(segl处的v轴投影,segr处的v轴投影);
if(segl处的v轴投影<=喷水范围+eps&&segr处的v轴投影>=-(喷水范围+eps)) return 1;
//有交集
}
return false;
}
//当前处理的角度范围是θ∈[l,r]
inline double 计算那个超级无敌难算的伤害(double l,double r)
{
double res=0;
int 周期min=ceil((初始角-r)/(2*pi)); //不早于攻击开始
int 周期max=floor((喷水时间+初始角-l)/(2*pi)); //不晚于攻击结束
for(int 周期=周期min;周期<=周期max;周期++)
{
double L=l-初始角+2*pi*周期; //过了若干周期之后的l,r角度
double R=r-初始角+2*pi*周期;
if(L>喷水时间) continue; //时间区间在喷水时间之后
if(R<0) continue; //时间区间在喷水时间前
L=max(L,(double)0);
R=min(R,(double)喷水时间);
if(L<R) res+=R-L;
}
return res;
}
int main()
{
// freopen("neuvillette.in","r",stdin);
// freopen("neuvillette.out","w",stdout);
cout.flags(ios::fixed);
cout.precision(保留多少位小数);
cin>>n>>x0>>y0>>喷水范围>>喷水时间;
周期数=ceil(喷水时间/(2*pi))+600;
初始角=change(atan2(y0,x0));
for(int i=1;i<=n;i++) cin>>poly[i].x>>poly[i].y;
vector<double> 临界角度=vector<double>{0,2*pi};
for(int i=1;i<=n;i++)
{
double 到原点距离=sqrt(poly[i].x*poly[i].x+poly[i].y*poly[i].y);
double 角度=change(atan2(poly[i].y,poly[i].x)); //该点的方位角
double 偏移=change(asin(喷水范围/到原点距离)); //和攻击射线的角度偏差
临界角度.push_back(change(角度+偏移));
临界角度.push_back(change(角度-偏移));
}
临界角度=unique(临界角度);
double 潮水啊,我已归来!=0;
//得到关键点之后就可以在区间上判断了
for(int i=0;i<(int)临界角度.size()-1;i++)
{
double l=临界角度[i];
double r=临界角度[i+1];
if(r-l<=eps) continue; //同一个角度
if(check((l+r)/2.0)) //能攻击到怪物
{
潮水啊,我已归来!+=计算那个超级无敌难算的伤害(l,r);
}
}
cout<<潮水啊,我已归来!;
return 0;
}
笑点解析:总的来说,这是一篇优秀的题解,主要思想正确,实现方案合理,稍作修改后可以成为很好的学习资料。那维莱特厨的用心程度可见一斑!
彩蛋环节:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号