长乐一中 CSP-S 2025 提高级模拟赛 Day1

赛时就中午打了一下，也没有多少分，就不说赛时怎么想的了。

A. 卡牌选取

题面

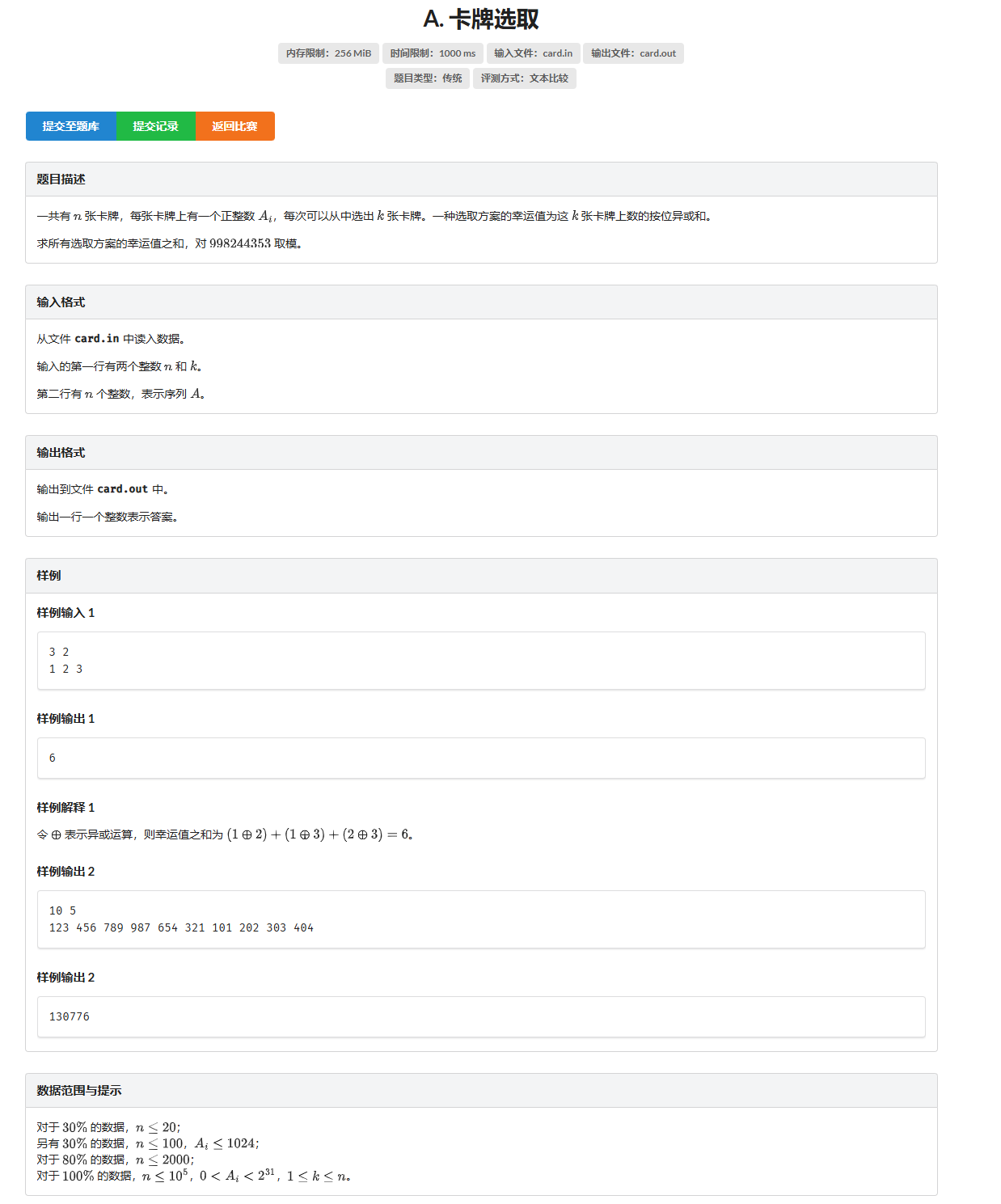
看到二进制、异或，想到拆位考虑。“\(n\) 个数中选 \(k\) 个数”可以想到组合数。

【trick】\(\operatorname{xor}_{i=1}^{n}a_i\) 的第 \(i\) 位为 \(1\)，当且仅当这 \(n\) 个数中有奇数个数该位为 \(1\)。

假设当前考虑到第 \(x\) 位，枚举一个 \(i\) 表示要 \(i\) 个数的该位为 \(1\)，然后怎么算贡献？应该要从 \(cnt1\) 个该位为 \(1\) 的数选出 \(i\) 个，从 \(cnt0\) 个该位为 \(0\) 的数中选 \(k-i\) 个，然后就有 \(C_{cnt1}^i C_{cnt0}^{k-i} \cdot 2^x\) 的贡献。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e5+7;
constexpr int mod=998244353;
int n,k;
ll f[N],nf[N],a[N];
inline ll ksm(ll a,ll b)
{
	ll s=1;
	while(b)
	{
		if(b&1) s=s*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return s;
}
inline void init(int len)
{
	f[0]=nf[0]=1;
	for(int i=1;i<=len;i++) f[i]=1ll*f[i-1]*i%mod;
	nf[len]=ksm(f[len],mod-2);
	for(int i=len-1;i>=1;i--) nf[i]=1ll*nf[i+1]*(i+1)%mod;
}
inline ll C(int _n,int _k)
{
	if(_n<_k) return 0;
	return 1ll*f[_n]*nf[_k]%mod*nf[_n-_k]%mod;
}
int main()
{
	freopen("card.in","r",stdin);
	freopen("card.out","w",stdout);
	cin>>n>>k; init(n);
	for(int i=1;i<=n;i++) cin>>a[i];
	ll ans=0;
	for(int x=0,cnt0,cnt1;x<=30;x++)   //现在是要考虑第x位 
	{
		cnt0=cnt1=0;
		for(int i=1;i<=n;i++) ((a[i]>>x)&1)?(++cnt1):(++cnt0);
		for(int i=1;i<=k;i+=2) ans=(ans+C(cnt1,i)*C(cnt0,k-i)%mod*ksm(2,x)%mod)%mod;
	}
	cout<<ans%mod;
	return 0;
}