2025 暑假集训 Day9

2025.8.13

题目相比前两场简单了很多，难度大概是黄黄紫紫？\(100+100+30+8=238 \operatorname{pts}\) 喜提 \(\operatorname{rank} 3/46\).

A. 连通块

给定一个 \(n\) 个点 \(m\) 条编号为 \(1 \sim m\) 的边的无向图，\(k\) 次询问，每一次询问如果拆除编号为 \(l \sim r\) 的边，那么图中剩下的连通块个数是多少。\(n \le 500,m \le 10000,k \le 20000,1 \le l \le r \le m\).

输入格式：第一行两个整数n,m，表示点数和边数。之后m行每行两个整数x,y，表示x与y之间有无向边。（按读入顺序给边编号，编号从1开始）一行一个整数k，表示Alice的破坏次数。之后k行，每行两个整数l,r。

输出格式：k行，每行一个整数。

样例

【样例输入】
6 5 
1 2 
5 4 
2 3 
3 1 
3 6 
6 
1 3 
2 5 
1 5 
5 5 
2 4 
3 3
【样例输出】
4 
5 
6 
3 
4 
2 

官方题解：每一个f[i]为一个并查集，记录只添加前i条边时，所有节点的联通情况。每一个g[i]也是一个并查集，记录只添加i—m条边时，所有节点的联通情况。对于每个询问只要把f[l-1]和g[r+1]合并即可。

官方题解看不懂，写一下考场做法：显然可以使用并查集，每一次询问的时候把编号为 \([1,l) \cup (r,n]\) 的边连上，然后直接数连通块即可。单次询问时间复杂度 \(O(n+m)\).

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=507;
constexpr int M=50009;
int n,m,l,r,fa[N];
struct edge{int u,v;}e[M];
int find(int u)
{
	return fa[u]==u?u:fa[u]=find(fa[u]);
}
inline int solve()
{
	for(int i=1;i<=n;i++) fa[i]=i;
	cin>>l>>r;
	for(int i=1;i<l;i++) fa[find(e[i].u)]=find(e[i].v);
	for(int i=r+1;i<=m;i++) fa[find(e[i].u)]=find(e[i].v);
	int cnt=0;
	for(int i=1;i<=n;i++) if(fa[i]==i) cnt++;
	return cnt;
}
int main()
{
//	freopen("data.in","r",stdin);
//	freopen("data.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>e[i].u>>e[i].v;
	int Q;cin>>Q;
	while(Q--) cout<<solve()<<'\n';
	return 0;
}

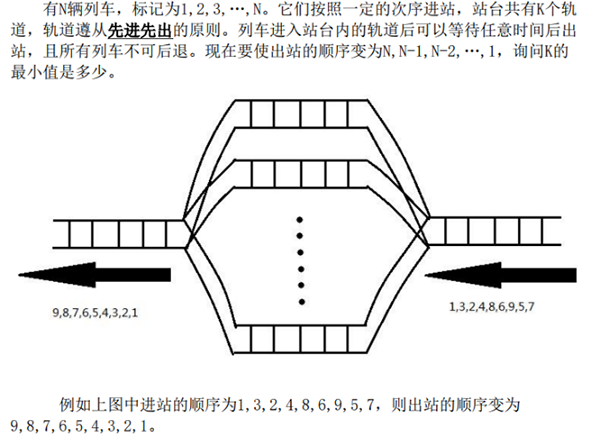
B. 列车调度

【样例1输入】
3
1 2 3
【样例1输出】
3
【样例2输入】
9
1 3 2 4 8 6 9 5 7
【样例2输出】
5

数据范围：\(n \le 10^5\).

首先可以发现每一个轨道都是一个队列。我们可以考虑像空当接龙一样，把大的编号的车放在队头，然后依次接上编号小的车。比如：对于样例 2，我们可以这样，然后出队的时候就可以从大到小出队了：

queue1:1
queue2:3,2
queue3:4
queue4:8,6,5
queue5:9,7

然后题目转化为原序列划分成最少的单调递减序列个数。根据 Dilworth 定理，最少的单调递减序列个数等于最长上升子序列的长度，然后就可以直接粘一个 \(O(n \log n)\) 求最长上升子序列的板子上来就拿到 AC 了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=100007;
constexpr int inf=998244353;
int n,a[N],b[N];
int main()
{
//	freopen("data.in","r",stdin);
//	freopen("data.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>n;
	for(int i=1;i<=n+1;i++) b[i]=inf;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++) *upper_bound(b+1,b+n+1,a[i])=a[i];
//	for(int i=1;i<=n;i++) cerr<<b[i]<<' ';
	int ans=0;
	while(b[ans]!=inf) ans++;
	cout<<ans-1;
	return 0;
}

C. 简单的玄学

在 \([0,2^n) \cap Z\) 中随机选取 \(m\) 个整形变量，设至少有两个变量取值相同的概率为 \(\dfrac{p}{q}\)（其中 \(p,q\) 互质），你需要输出 \(a,b\) 对 \(10^6+3\) 取模的值。\(n,m \le 10^{18}\).

【样例1输入】
3 2
【样例1输出】
1 8
【样例2输入】
1 3
【样例2输出】
1 1
【样例3输入】
4 3
【样例3输出】
23 128

先给出一个引理：

引理 1：\(\forall 1 \le a < 2^n,a,2^n-a\) 中 \(2\) 的次数相同。

证明：设 \(a=x2^k\) 其中 \(x\) 不含 \(2\) 的因子（\(x\) 为奇数），则：

\[2^n-a=2^n-(x2^k)=2^k \cdot 2^{n-k}-2^k \cdot x=2^k(2^{n-k}-x) \]

因为 \(2^{n-k}\) 为偶数，\(x\) 为奇数，所以 \(2^{n-k}-x\) 为奇数，不含 \(2\) 的因子，所以：

\[2^n-a=2^k(2^{n-k}-x),a=2^k \cdot x \]

可以发现两者 \(2\) 的次数都为 \(k\)。故原命题得证。

首先可以想到这个题和生日悖论是一个做法的。“至少有两个变量取值相同”和“所有变量取值都不相同（记为事件 \(A\)）”是一对对立事件。对于第一个变量，不和其他变量取值相同的概率是 \(1\)，第二个变量不和其他变量取值相同的概率就是在 \([0,2^n)\) 中选出一个不等于第一个变量的数，有 \(2^n-1\) 种选择，所以概率为 \(\dfrac{2^n-1}{2^n}\). 第三、第四和后面的变量都同理。所以我们可以得出：

\[P(A)=\prod_{i=0}^{m-1}\dfrac{2^n-i}{2^n}=\dfrac{\prod_{i=1}^{m-1} 2^n-i}{2^{n(m-1)}}=\dfrac{\prod_{i=2^n-m+1}^{2^n-1} i}{2^{n(m-1)}} \]

分母很好算，一个快速幂搞定。分子怎么算？考虑到当 \(m > mod\) 时，分子的乘法式子中一定有一项 \(mod\)，取模之后直接变成 \(0\) 了。所以当 \(m>mod\) 时分子直接等于 \(0\) 即可。

怎么约分？分母只含质因子 \(2\)，所以分子也只能约 \(2\)。由引理 1，\(\forall 1 \le a < 2^n,a,2^n-a\) 中 \(2\) 的次数相同（证明可看下面的引理），所以 \(\prod_{i=1}^{m-1} 2^n-i\) 中 \(2\) 的次数就等于 \(\prod_{i=1}^{m-1} i=(m-1)!\) 中 \(2\) 的次数。如何求 \((m-1)!\) 中 \(2\) 的次数？考虑使用勒让德公式。

勒让德公式：设 \(p\) 为质数，\(n!\) 中 \(p\) 的次数 \(e\) 满足如下公式：

\[e=\sum _{k=1}^\infty \left\lfloor \dfrac{n}{p^k} \right\rfloor \]

所以可以在 \(O(\log m)\) 的时间复杂度内求出 \((m-1)!\) 中 \(2\) 的次数。然后约分就好了

最后的答案就是 \(1-P(A)\)，设 \(P(A)=\dfrac{p}{q}\)，那么最后的答案就是 \(1-P(A)=\dfrac{q-p}{q}\) 约分后的结果。