2025 暑假集训 Day4
2025.8.7
Day 4:树状数组+线段树
树状数组
修改和查询的操作懒得写了……直接粘个板子,时间复杂度是 \(O(\log n)\) 的:
inline void modify(int x,int k) //位置x的数增加k
{
for(int i=x;i<=M;i+=lowbit(i)) c[i]+=k;
}
inline int query(int x) //查询1~x所有数的和
{
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=c[i];
return res;
}
stars
【题目】 给定 \(n\) 个点,定义每个星星的等级是在该点左下方(含正左和正下)的星星的数目,试统计每个等级有多少个星星。(\(n \le 15000,0 \le x,y \le 32000\))
【样例输入】
5
1 1
5 1
7 1
3 3
5 5
【样例输出】
1
2
1
1
0
二维偏序模板题。题目想让我们找出满足 \(x_i \le x_j\) 且 \(y_i \le y_j\) 的 \((i,j)\),那么先用排序把第一维搞定,然后第二维开一个数组 \(a_i\),按照排序的顺序把这 \(n\) 个星星扫一遍,扫到第 \(i\) 个星星时,这个星星的等级就是 \(a_1 \sim a_{y_{i}}\),接着让 \(a_{y_i}\) 加一就好了。\(a_i\) 数组要求单点修改和区间查询两种操作,用树状数组可以让每一种操作的时间复杂度都是 \(O(\log n)\)。注意树状数组遇到下标为 \(0\) 的情况会死循环,所以星星的坐标都要加一。
补充:关于“偏序”(参考资料:洛谷专栏 @abensyl 偏序问题与 CDQ 分治):
偏序关系:设 \(R\) 为集合 \(A\) 上的一个二元关系。如果该关系满足以下三个条件,则为“偏序关系”:
- 自反性:\(\forall x \in A,x \operatorname{R} x\);
- 反对称性:\(\forall x,y \in A\),若 \(x \operatorname{R} y\) 且 \(y \operatorname{R} x\),则 \(x=y\);
- 传递性:\(\forall x,y,z \in A\),若 \(x \operatorname{R} y\) 且 \(y \operatorname{R} z\),则 \(x \operatorname{R} z\)。
没有自反性的偏序关系叫“拟序关系”,比如 \(\ge,\le\) 就是偏序关系,\(>,<\)就是拟序关系。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=15007;
constexpr int M=32005;
int n,c[M+10];
int cnt[N];
struct node{int x,y,id;}p[N];
inline int lowbit(int x)
{
return x&-x;
}
inline void modify(int x,int k)
{
for(int i=x;i<=M;i+=lowbit(i)) c[i]+=k;
}
inline int query(int x)
{
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=c[i];
return res;
}
int main()
{
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&p[i].x,&p[i].y);
p[i].x++; p[i].y++; //防止出现0
p[i].id=i;
}
sort(p+1,p+n+1,[&](node A,node B){
if(A.x==B.x) return A.y<B.y;
else return A.x<B.x;
});
for(int i=1;i<=n;i++)
{
cnt[query(p[i].y)]++;
modify(p[i].y,1);
}
for(int i=0;i<n;i++) printf("%d\n",cnt[i]);
return 0;
}
/*
二维偏序板子题
x[i]<=x[j] 且 y[i]<=y[j]
*/
小陶的疑惑
【题目】 给出一个有 \(n\) 个元素的序列 \(a_1,a_2,\cdots,a_n\),进行 \(m\) 次操作,操作有两种类型:
1 x y k:让 \(a_x \sim a_y\) 的数都加上 \(k\);2 x y:求 \(\sum _{i=x}^ya_i\)。
【样例输入】
10 5
1 2 3 4 5 6 7 8 9 10
2 4 4
2 1 10
2 2 4
1 3 6 3
2 2 4
【样例输出】
4
55
9
15
区间修改区间查询,一看好像是要用线段树,但是线段树 太难写了 常数太大,所以考虑树状数组。
首先考虑原序列给 \(a_i\) 做差分得到差分数组 \(d_i\)。由差分数组的性质,得:
所以 \(a_i\) 的前缀和为:
找规律发现,这个式子里面 \(d_1\) 出现了 \(p\) 次,\(d_2\) 出现了 \((p-1)\) 次,\(p_i\) 出现了 \((p-i+1)\) 次,故 \(\sum_{i=1}^p \sum_{j=1}^i d_j\) 可以变形为:
发现上式中的 \(\sum_{i=1}^p\) 都可以用树状数组维护,所以可以开两个树状数组 \(c1,c2\) 分别维护 \(d_i\) 和 \(d_i \cdot i\),操作 \(1\) 区间修改的时候 \(c1_x \gets c1_x+d,c1_{y+1} \gets c1_{y+1}-d,c2_x \gets c2_x+dx,c1_{y+1} \gets c1_{y+1}-[d(r+1)]\),然后查询可以用 \(\sum_{i=1}^p a_i=(p+1)\sum_{i=1}^p d_i-\sum_{i=1}^p d_i \cdot i\) 这个 \(a_i\) 的前缀和公式就好了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=2e5+7;
int n,m;
ll c1[N],c2[N];
inline int lowbit(int x)
{
return x&-x;
}
inline void modify1(int x,ll k)
{
for(int i=x;i<=n;i+=lowbit(i)) c1[i]+=k;
}
inline void modify2(int x,ll k)
{
for(int i=x;i<=n;i+=lowbit(i)) c2[i]+=k;
}
inline void modify(int l,int r,ll k)
{
modify1(l,k); modify1(r+1,-k);
modify2(l,l*k); modify2(r+1,-1ll*((r+1ll)*k));
}
inline ll query1(int x)
{
ll res=0;
for(int i=x;i;i-=lowbit(i)) res+=c1[i];
return res;
}
inline ll query2(int x)
{
ll res=0;
for(int i=x;i;i-=lowbit(i)) res+=c2[i];
return res;
}
inline ll query_pre(int x) //查询a的前缀和
{
return (x+1)*query1(x)-query2(x);
}
inline ll query(int l,int r)
{
return query_pre(r)-query_pre(l-1);
}
int main()
{
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin>>n>>m;
ll t;
for(int i=1;i<=n;i++)
{
cin>>t;
modify(i,i,t);
}
int op,x,y;
ll k;
while(m--)
{
cin>>op>>x>>y;
if(op==1)
{
cin>>k;
modify(x,y,k);
}
else cout<<query(x,y)<<'\n';
}
cout.flush(); //文件输出要把这个加上
return 0;
}
/*
a原序列 d差分序列 d的前缀和序列是a
sum(i=1~p)a[i]=sum(i=1~p)sum(j=1~i)d[j]
=sum(i=1~p)d[i]*(p-i+1)={(p+1)*sum(i=1~p)d[i]}+{sum(i=1~p)d[i]*i}
用两个树状数组(c1,c2)维护d[i]和d[i]*i
*/
线段树
懒得写了,直接看板子
需要注意的是,有些东西需要按照题目修改:
modify(在这个板子里简写成了M)的if(l<=tr[u].l&&tr[u].r<=r)部分,需要改成“执行修改操作之后,相关数值和懒标记该如何变动”,比如线段树维护区间和的例子,在执行修改操作之后应该把sum和lazy相应修改;push_up函数,需要把部分答案合并,比如求和、取max等;push_down函数,需要把懒标记下放。
还有很多要注意的点,需要看题目后随机应变。
例题一
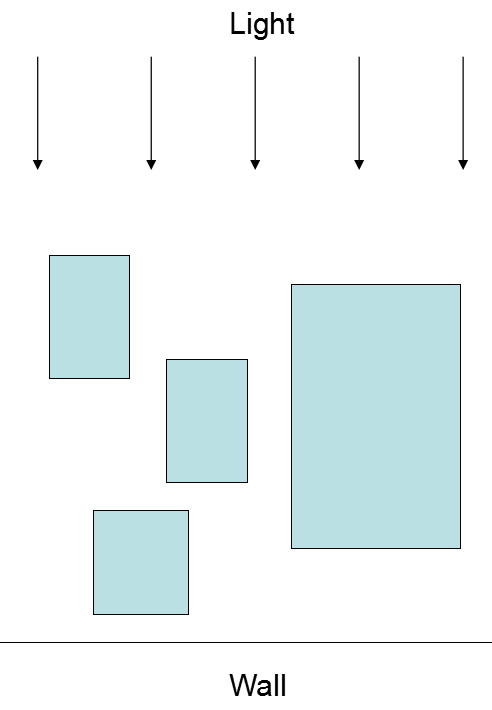
宽度为 \(m\) 的桌子上零散地放着 \(m\) 个盒子,桌子的后方是一堵墙。如右图所示。现在从桌子的前方射来一束平行光, 把盒子的影子投射到了墙上。问影子的总宽度是多少?
【样例输入】
20 //桌面总宽度
4 //盒子数量
1 5
3 8
7 10
13 19
【样例输出】
15
思路懒得写了直接看代码吧
#include<bits/stdc++.h>
#define ls (u<<1)
#define rs (u<<1|1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e5+7;
int n,m;
bool vis[N<<2];
void modify(int u,int l,int r,int a,int b) //将区间[a,b]打上标记
{
int mid=(l+r)>>1;
if(vis[u]==1) return;
if(l==a&&r==b) vis[u]=1;
else if(b<=mid) modify(ls,l,mid,a,b); //全都在左子树
else if(a>=mid) modify(rs,mid,r,a,b); //全都在右子树
else modify(ls,l,mid,a,mid),modify(rs,mid,r,mid,b); //左右子树都有
}
int query(int u,int l,int r) //查询区间[a,b](题目只会查询一次[1,n],(a,b)=(l,r)所以直接省去了a,b)
{
int mid=(l+r)>>1;
if(vis[u]) return (r-l);
if(r-l>1) return query(ls,l,mid)+query(rs,mid,r);
else return 0;
}
int main()
{
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1,a,b;i<=m;i++)
{
scanf("%d%d",&a,&b);
modify(1,1,n,a,b);
}
printf("%d",query(1,1,n));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号