【初高衔接】等式变形、不等式解法

B 站视频 P2-P3

乘法公式

基本公式

• \((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
• \((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
• \(a^3+b^3=(a+b)(a^2+b^2-ab)\)
• \(a^3-b^3=(a-b)(a^2+b^2+ab)\)

根号套根号，凑完全平方

完全平方公式：\((a \pm b)^2=a^2 \pm 2ab+b^2\)

例：\(\sqrt{5-2\sqrt{6}}\)，可以把 \(2\sqrt{6}\) 看成完全平方公式里面的 \(2ab\)，拆一下可以得到 \(2\sqrt{6}=2 \times \sqrt{2} \times \sqrt{3}\)（对应公式里面的 \(a=\sqrt2,b=\sqrt3\)），发现 \(\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2=5\)，于是：

\[\begin{align*} & \sqrt{5-2\sqrt{6}} \\ &= \sqrt{\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2-2 \times \sqrt{2} \times \sqrt{3}} \\ &= \sqrt{(\sqrt{2}-\sqrt{3})^2} \\ &= \left| \sqrt{2}-\sqrt{3} \right| \\ &= \sqrt{3}-\sqrt{2} \end{align*} \]

注意绝对值不要漏掉。

如果遇到像 \(\sqrt{4-\sqrt{15}}\) 这种没有二倍的式子，可以先提取出一个 \(\dfrac{1}{2}\) 出来，变成 \(\sqrt{\dfrac{1}{2}(8-2\sqrt{15})}\) 就好做了。

同样要注意绝对值不要丢掉。

因式分解

公式法

直接用各种乘法公式搞一搞就搞出来了。

十字相乘

如果遇到了二次三项式，可以尝试用十字相乘。\(Ax^2+Bx+C=(ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)，其中大写的字母题目会给出来，小写的 \(a,b,c,d\) 就要自己去试试了。

\[\begin{array}{c} ax & & b \\ & \huge\times & \\ cx & &d \\ \end{array} \]

要找左边的两个 \(a,c\) 相乘结果等于 \(A\)，右边两个 \(b,d\) 相乘结果等于 \(C\)，十字交叉相乘（\(ad+bc\)）的结果等于 \(B\)，然后最后的结果横着写下来 \((ax+b)(cx+d)\)。

一句话就是：横着写，竖着凑，斜着乘

如果题目中有一大堆字母（\(x,y,a,b\)）之类的，可以先找一个字母出来当成主元，其他全部当成常量，一步一步因式分解。

猜根法因式分解

看到题目中一个 \(ax^3+bx^2+cx+d\)，出现了三次，可以考虑一下令 \(ax^3+bx^2+cx+d=0\)，然后使用虚空终端连接世界树，让世界树帮你算出一个根 瞪眼法瞪出一个根出来（一般都是 \(\pm 1,\pm 2\)，实在恶心人的题目有可能出现 \(\pm \dfrac12\) 这一类），假设用瞪眼法瞪出的根为 \(t\)，那么原式一定包含一个因式 \((x-t)\)，具体可参考因式分解解一元二次方程时 \((x-x_1)(x-x_2)=0\) 时，方程的根就为 \(x_1,x_2\)。之后就可以使用长除法把原式除以 \((x-t)\)，再对剩下的式子因式分解（一般这个剩下的式子可以用十字相乘法因式分解）

长除法其实就是把小学生做的那个竖式除法一个算法，只不过把数字换成了式子。试商的思路：比如写到 \(\dfrac{x^3+x^2}{x-1}\) 这一步时，此时应该要把 \(x^3\) 消掉，我到底要让 \(x-1\) 乘以谁才能把这个 \(x^3\) 消掉呢？肯定是 \(x^2\) 啊，因为 \(x^2(x-1)=x^3-x^2\)，然后 \((x^3+x^2)-(x^3-x^2)\) 就可以发现把 \(x^3\) 减掉了。

不等式

一元二次不等式

\(ax^2+bx+c>0\)，把不等式直接看成一个二次函数，\(y=ax^2+bx+c\)，先算出二次函数与 \(x\) 轴的交点（解一元二次方程），然后根据图象判断它在 \(x\) 轴上方的部分是哪里。小于号、小于等于号、大于等于号同理。

总结：一元二次不等式先画图象，再用数形结合的方法解。

分式不等式

• \(\frac ab>0 \iff ab>0\)（\(a,b\) 同号）
• \(\frac ab<0 \iff ab<0\)（\(a,b\) 异号）

如果遇到不等号另一侧不是 \(0\) 的情况就移项通分一下。

注意，分母不能为零，写题的时候要注意一下。

高次不等式

形如 \((x-a_1)^{b_1}(x-a_2)^{b_2}(x-a_3)^{b_3} \cdots (x-a_n)^{b_n}>/</\ge/\le0\) 这样的不等式可以使用穿针引线法，先假设原式等于零求出根来，然后利用口诀 奇穿偶不穿 （即指数为奇数的时候要传过去，偶数的时候不要穿过去，为什么？画一个一次函数和二次函数的图象就知道了）画出图象，最后看函数图像位于 \(x\) 轴上方/下方的部分就可以得出不等式解集。

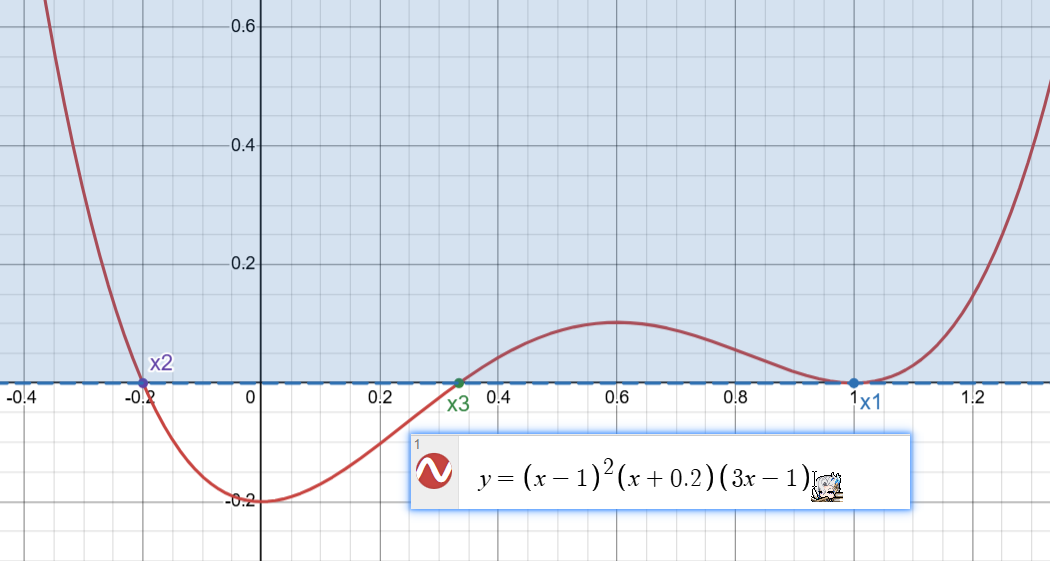
比如 \(y=(x-1)^2(x+0.2)(3x-1)\)，令 \(y=0\) 得到三个根 \(x_1=1,x_2=-0,2,x_3=\frac13\)，\(x_1\) 对应的是 \((x-1)^2\)，次数为 \(2\) 是偶数，所以要传过去，但是 \(x_2,x_3\) 对应的因式都是奇数次（\(1\) 次），所以不用穿。

如果要求 \((x-1)^2(x+0.2)(3x-1)>0\)，则看 \(x\) 轴上方的部分。如图：

绝对值不等式

如果遇到了形如 \(|a|>|b|\) 这种式子，可以使用 \(|a|>|b| \iff a^2>b^2\) 这个结论转化成一元二次不等式，然后进行求解。小于号等同理。

如果遇到了只有一边有绝对值的，可以分情况讨论。

有些也可以按照几何定义理解，\(|a|\) 表示的是数轴上 \(a\) 所对应的数到原点的距离，\(|a|>2 \to a<-2\) 或 \(a>2\)。

根式不等式

遇到了像 \(\sqrt{a}<b\) 这种式子之后，先平方一下，然后考虑三个约束条件：

• \(a<b^2\)，没啥好解释了，跟着原式来的；
• \(a \ge 0\)，平方根具有非负性，总不能给你高出一个虚数出来对吧；
• \(b>0\)，显然 \(\sqrt{a}\) 是非负数，\(b\) 比一个非负数还大，那么肯定要 \(>0\)。

最后解出来即可。