ABC406

$$\text{ABC406} : 比赛传送门$$

A - Not Acceptable

高桥有一份报告，截止时间是 2025年5月17日 \(A\) 点 \(B\) 分。他实际提交的时间是 2025年5月17日 \(C\) 点 \(D\) 分。
题目保证 \(A\) 点 \(B\) 分 和 \(C\) 点 \(D\) 分 是不同的时间点。

如果高桥在截止时间之前提交了报告，则输出 Yes，否则输出 No。

首先发现到题目 o'clock 中的 clock 是闹钟的意思，闹钟的工作需要电，题目中的 Acceptable 前两个字 AC 是交流电的意思，然后联想到电学公式 \(I = \dfrac{U}{R}\)，所以直接欧姆定律秒了。送分题无需多解释。

Submission #65848723.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=0;
int a,b,c,d;
inline bool k()
{
    if(a==c) return b>d;
    else return a>c;
}
int main()
{
    cin>>a>>b>>c>>d;
    puts(k()?"Yes":"No");
	return 0;
}

B - Product Calculator

高桥有一个计算器，初始显示数字为 \(1\)。
他将对这个计算器进行 \(N\) 次操作。
在第 \(i\) 次操作中（\(1 \leq i \leq N\)），他会将当前显示的数字乘以一个正整数 \(A_i\)。
然而，计算器最多只能显示 \(K\) 位数。如果乘法运算的结果有 \((K+1)\) 位或更多位数，计算器将显示 \(1\)；否则，结果会正确显示。

求经过 \(N\) 次操作后，计算器上显示的数字。

这题需要用到焦耳定律求计算器产生的热量，\(Q=I^2Rt\)，注意不是纯电阻电路。

Submission #65869280.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=0;
int main()
{
    int n,k;
    cin>>n>>k;
    ull s=1,lim=1;
    for(int i=1;i<=k;i++) lim*=10;
    lim--;
    // cerr<<lim;
    while(n--)
    {
        ull x;
        cin>>x;
        if(x>lim/s) s=1;
        else s=s*x;
    }
    cout<<s;
	return 0;
}
/*
a*b>=lim b>=lim/a
*/

C - ~

对于一个整数序列 \(A = (A_1, A_2, \ldots, A_{|A|})\)，如果它同时满足以下四个条件，我们称其为波浪形序列：

1. 序列长度 \(|A|\) 至少为 \(4\)。
2. 满足 \(A_1 < A_2\)。
3. 存在唯一一个整数 \(i\)（\(2 \leq i < |A|\)），使得 \(A_{i-1} < A_i > A_{i+1}\)（这个点即为波峰）。
4. 存在唯一一个整数 \(i\)（\(2 \leq i < |A|\)），使得 \(A_{i-1} > A_i < A_{i+1}\)（这个点即为波谷）。

给定一个排列 \(P = (P_1, P_2, \ldots, P_N)\)（即 \((1, 2, \ldots, N)\) 的某种排列），求 \(P\) 中所有满足波浪形条件的子串的数量。

首先我们可以先找出“波峰”和“波谷”的位置 \(mx_i\) 和 \(mn_i\)（为了方便，分别在序列最前和最后加一个极大和极小值）。

由题意知，一个波浪形序列的形状可以分成五个部分：（最远可达上一个波谷）第一次上升→波峰→下降→波谷→第二次上升（最远可达下一个波峰）。

记 \(k\) 为波峰和波谷的数量（显然波峰和波谷的数量必定是相等的），对于每一个 \(i(1 < i < k)\)，波浪形序列的第一次上升部分可以是 \(mn_i \sim mx_i-1\)，第二次上升部分可以是 \(mn_{i+1} \sim mx_{i+1}\)。

在第一和二次上升部分的取值范围内分别找出任意两个下标，就可以组成一种方案。根据乘法原理，当前波峰对答案的贡献就是这两个部分数的个数的乘积。

比如样例三的数据可以画成如下的图：

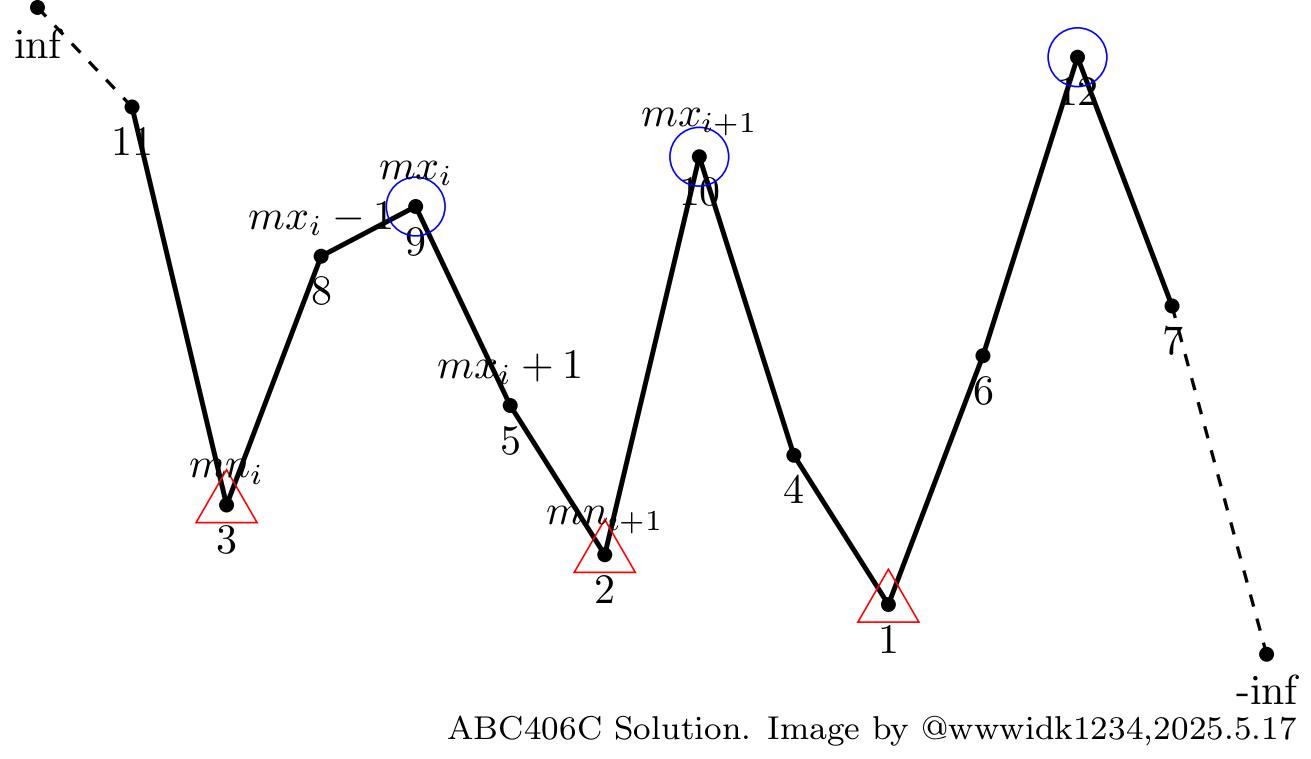
其中用圆圈圈住的为波峰，用三角形圈住的为波谷。在波峰 \(9\) 的左边的 \(3,8\) 为第一次上升部分，有 \(2\) 个数，在波谷 \(2\) 右边的 \(10\) 为第二次上升部分，有 \(1\) 个数。波峰 \(9\) 对答案的贡献就是 \(2 \times 1=2\)。

Submission #65914061.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=3e5+7;
constexpr int inf=12181218;
int n;
int a[N];
vector<int> mx,mn; //波峰和波谷
inline ll cnt(int l,int r)
{
    return r-l+1;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    a[0]=inf,a[n+1]=-inf;
    for(int i=1;i<=n;i++)
    {
        if(a[i-1]<a[i]&&a[i]>a[i+1]) mx.push_back(i);
        if(a[i-1]>a[i]&&a[i]<a[i+1]) mn.push_back(i);
    }
    int k=mx.size();
    ll ans=0;
    // for(int i=0;i<k;i++) cerr<<mn[i]<<' '<<mx[i]<<'\n';
    for(int i=0;i<k-1;i++)
    {
        // cerr<<mx[i]<<' '<<mn[i]<<' '<<mx[i+1]<<'\n';
        // cerr<<cnt(mn[i],mx[i]-1)<<' '<<(cnt(mn[i+1]+1,mx[i+1]))<<'\n';
        ans+=(cnt(mn[i],mx[i]-1))*(cnt(mn[i+1]+1,mx[i+1]));
    }
    cout<<ans;
    return 0;
}

D - Garbage Removal

有一个 \(H\) 行 \(W\) 列的网格。用 \((i, j)\) 表示从上往下第 \(i\) 行、从左往右第 \(j\) 列的单元格。

网格上有 \(N\) 个垃圾，第 \(i\) 个垃圾位于单元格 \((X_i, Y_i)\)。

现在需要依次处理 \(Q\) 个查询，每个查询是以下两种类型之一：

• 类型 1：输入格式为 1 x。查询第 \(x\) 行的垃圾数量，并清除该行的所有垃圾（即删除该行上的所有垃圾）。
• 类型 2：输入格式为 2 y。查询第 \(y\) 列的垃圾数量，并清除该列的所有垃圾（即删除该列上的所有垃圾）。

感觉这个 D 题比 C 题还简单。怎么感觉这个题怎么熟悉，总感觉这题目在哪里做过，感觉像是在 2023 年暑假的一场洛谷公开赛写过一道类似的题目，但是实在记不起来也找不到了。难道是初三英语书上说的 déjà vu？

首先 \(H,W \le 2 \times 10^5\) 显然不能直接暴力枚举的。考虑使用 C++ 中的 set 维护垃圾。设 \(hang_i\) 表示第 \(i\) 行中有哪些列有垃圾，第 \(lie_i\) 表示第 \(i\) 行中有哪些列有垃圾。

如果要清除第 \(x\) 行内的所有垃圾，可以将 \(hang_x\) 扫一遍，找到每一个垃圾所在的列 \(t\)，最后将 \(lie_t\) 中的 \(x\) 删除。删除列的操作同理。

由于 set 根据给定值删除元素的时间复杂度是对数级别的，而且一共最多也只有 \(2 \times 10^5\) 个垃圾，所以该方法不会超时，可以 AC 本题。

Submission #65917494.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=2e5+7;
set<int> hang[N],lie[N];  //hang[i]存放第i行的第几列有垃圾
inline int delhang(int x)
{
    int ans=hang[x].size();
    for(int t:hang[x])
    {
        lie[t].erase(x);
    }
    hang[x].clear();
    return ans;
}
inline int dellie(int x)
{
    int ans=lie[x].size();
    for(int t:lie[x])
    {
        hang[t].erase(x);
    }
    lie[x].clear();
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n,m,c;
    int u,v;
    cin>>n>>m>>c;
    for(int i=1;i<=c;i++)
    {
        cin>>u>>v;
        hang[u].insert(v);
        lie[v].insert(u);
    }
    int Q;
    cin>>Q;
    while(Q--)
    {
        int op,x;
        cin>>op>>x;
        if(op==1) cout<<delhang(x)<<'\n';
        else cout<<dellie(x)<<'\n';
    }
    return 0;
}

题外话：

找到了，那一题原来是 洛谷 P9583 「MXOI Round 1」涂色，做法没有什么太大的关系，但是可能是和学校 2024 年 CSP-J 模拟赛第四题人才市场（原题：洛谷P2286 [HNOI2004] 宠物收养场）这两题的记忆混合了，因为宠物收养场这一题老师给的 std 就是 set。然后两题思路一混合就是现在的记忆了。