2025 提高班寒假作业
PS:原本是寒假作业的,结果一整个寒假没搞 OI,开学之后中午跑去机房里火速补。作业题目均为 CSP-S 历年真题。
(2021·提高·T1) 廊桥分配
题目
一共有 \(n\) 个廊桥,廊桥的使用遵循“先到先得”的原则,即每架飞机抵达后,如果相应的区(国内/国际)还有空闲的廊桥,就停靠在廊桥,否则停靠在远机位(远机位的数量充足)。现给定未来一段时间飞机的抵达、离开时刻(不存在两架飞机同时抵达的情况),将 \(n\) 个廊桥分配给国内区和国际区,使停靠廊桥的飞机数量最多,并输出这个最大值。
思路
设 \(ans_i\) 表示国内/国际分配了 \(i\) 个廊桥后有 \(ans_i\) 架飞机可以停靠,我们只需开两个优先队列,一个是等待离开的飞机(wait),一个是待分配的廊桥(q,一开始的元素为 \(1 \sim n\)),之后每一个航班扫一遍,如果等待起飞队列不为空且离开时间比当前航班到达时间早,那么飞机起飞,归还廊桥。如果还有多余的廊桥,就继续分配。最后用前缀和维护一下 ans 数组即可。答案为 \(\max_{i=0}^{n}(ans(国内)_i,ans(国际)_{n-i})\).
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e5+7;
struct plane
{
int l,r;
bool operator<(plane B){return l<B.l;}
}a[N],b[N]; //a国内 b国际
int n,ma,mb;
int ansa[N],ansb[N]; //ans[i]:国内/国际分配了i个廊桥后有ans[i]架飞机可以停靠
inline void solve(plane a[],int m,int ans[])
{
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> wait;
//等待离开的飞机,pair存放离开的时间和占用的廊桥编号
priority_queue<int,vector<int>,greater<int>> q; //待分配的廊桥
for(int i=1;i<=n;i++) q.push(i); //一开始廊桥全都是空的
for(int i=1;i<=m;i++) //每个航班扫一遍
{
//如果等待起飞队列不为空,且离开时间<=当前航班到达时间,起飞
while(!wait.empty()&&wait.top().first<=a[i].l)
{
q.push(wait.top().second); //把廊桥还回去
wait.pop(); //起飞
}
if(!q.empty()) //如果还有多余的廊桥,就继续分配
{
int id=q.top(); //找出第一个廊桥
q.pop();
ans[id]++; //分配
wait.push({a[i].r,id}); //占用一个廊桥
}
}
for(int i=1;i<=n;i++) ans[i]+=ans[i-1]; //前缀和优化
}
int main()
{
freopen("airport.in","r",stdin);
freopen("airport.out","w",stdout);
scanf("%d%d%d",&n,&ma,&mb);
for(int i=1;i<=ma;i++) scanf("%d%d",&a[i].l,&a[i].r);
for(int i=1;i<=mb;i++) scanf("%d%d",&b[i].l,&b[i].r);
sort(a+1,a+ma+1);
sort(b+1,b+mb+1);
solve(a,ma,ansa);
solve(b,mb,ansb);
int maxans=-1218;
for(int i=0;i<=n;i++) maxans=max(maxans,ansa[i]+ansb[n-i]);
printf("%d",maxans);
return 0;
}
(2022·提高·T2) 策略游戏
题目
题目大意
小 L 和小 Q 在玩一个策略游戏。游戏基于两个数组 \(A\) 和 \(B\),通过它们生成一个矩阵 \(C\),其中 \(C_{ij}=A_i×B_j\)。矩阵的大小为 \(n \times m\)。
游戏共有 \(q\) 轮,每轮会给出四个参数 \(l_1,r_1,l_2,r_2\),定义了一个子矩阵的范围:行范围为 \(l_1\) 到 \(r_1\),列范围为 \(l_2\) 到 \(r_2\)。
在每轮游戏中:
- 小 L 先选择一个行下标 \(x\)(满足 \(l_1 \le x \le r_1\))。
- 小 Q 再选择一个列下标 \(y\)(满足 \(l_2 \le y \le r_2\))。
- 游戏的得分是 \(C_{xy}\)。
- 小 L 的目标是让得分尽可能大,而小 Q 的目标是让得分尽可能小。两人都会采取最优策略。
- 任务是计算每轮游戏中,按照两人的最优策略,最终的得分是多少。
思路
贪心+ST 表。等下再补
代码
//5oiR5piv6YKj57u06I6x54m555qE54uX
//6Im+5bCU5rW35qOu55qE54uX5bCx5piv5oiR
//6Kej5a+GYmFzZTY05aW9546p5ZCX
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e5+10;
int n,m,q;
constexpr ll inf=numeric_limits<long long>::max();
constexpr ll infmin=numeric_limits<long long>::min();
int a[N],b[N];
ll amax[N][19],amin[N][19],azmin[N][19]/*a正数(包括0)最小值*/,afmax[N][19]/*a负数最大值*/;
ll bmax[N][19],bmin[N][19];
template <typename T>
inline void read(T &x){x=0;char ch=getchar();bool f=0;while(ch<'0'||ch>'9'){if(ch=='-')f=1;ch=getchar();}while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();if(f)x=-x;}
template <typename T,typename ...Args>
inline void read(T &tmp,Args &...tmps){read(tmp);read(tmps...);}
template <typename T,typename ...Args>
inline void readn(T a[],int _){for(int i=1;i<=_;i++) read(a[i]);}
template <typename T>
inline void write(T x){if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10+48);}
template <typename T,typename ...Args>
inline void write(T tmp,Args ...tmps){write(tmp);putchar(' ');write(tmps...);}
template <typename ...Args>
inline void writeln(Args ...tmps){write(tmps...);putchar('\n');}
ll qamax(int l,int r)
{
int x=log2(r-l+1);
return max(amax[l][x],amax[r-(1<<x)+1][x]);
}
ll qamin(int l,int r)
{
int x=log2(r-l+1);
return min(amin[l][x],amin[r-(1<<x)+1][x]);
}
ll qbmax(int l,int r)
{
int x=log2(r-l+1);
return max(bmax[l][x],bmax[r-(1<<x)+1][x]);
}
ll qbmin(int l,int r)
{
int x=log2(r-l+1);
return min(bmin[l][x],bmin[r-(1<<x)+1][x]);
}
ll qafmax(int l,int r)
{
int x=log2(r-l+1);
return max(afmax[l][x],afmax[r-(1<<x)+1][x]);
}
ll qazmin(int l,int r)
{
int x=log2(r-l+1);
return min(azmin[l][x],azmin[r-(1<<x)+1][x]);
}
inline ll solve(int l1,int r1,int l2,int r2)
{
ll mxa=qamax(l1,r1),mna=qamin(l1,r1);
ll mxb=qbmax(l2,r2),mnb=qbmin(l2,r2);
ll ans;
if(mna>=0) //a正
{
if(mnb>=0) ans=mxa*mnb;//b正
else if(mxb<0) ans=mna*mnb; //b 0/负
else ans=mna*mnb;
}
else if(mxa<0) //a负
{
if(mnb>=0) ans=mxa*mxb; //b正
else if(mxb<0) ans=mna*mxb; //b负
else ans=mxa*mxb;
}
else //a正+负
{
if(mnb>=0) ans=mxa*mnb; //b正
else if(mxb<0) ans=mna*mxb;
else
{
long long aa=qazmin(l1,r1);
long long bb=qafmax(l1,r1);
ans=max(aa*mnb,bb*mxb);
}
}
return ans;
}
int main()
{
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
read(n,m,q);
for(int i=1;i<=n;i++)
{
read(a[i]);
amax[i][0]=amin[i][0]=a[i];
azmin[i][0]=(a[i]>=0?a[i]:inf);
afmax[i][0]=(a[i]<0?a[i]:infmin);
}
for(int i=1;i<=m;i++)
{
read(b[i]);
bmax[i][0]=bmin[i][0]=b[i];
}
int logn=log2(n);
for(int j=1;j<=logn;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
amax[i][j]=max(amax[i][j-1],amax[i+(1<<(j-1))][j-1]),
bmax[i][j]=max(bmax[i][j-1],bmax[i+(1<<(j-1))][j-1]),
amin[i][j]=min(amin[i][j-1],amin[i+(1<<(j-1))][j-1]),
bmin[i][j]=min(bmin[i][j-1],bmin[i+(1<<(j-1))][j-1]),
azmin[i][j]=min(azmin[i][j-1],azmin[i+(1<<(j-1))][j-1]),
afmax[i][j]=max(afmax[i][j-1],afmax[i+(1<<(j-1))][j-1]);
while(q--)
{
int l1,r1,l2,r2;
read(l1,r1,l2,r2);
writeln(solve(l1,r1,l2,r2));
}
return 0;
}
(2023·提高·T1) 密码锁
题目
某神秘人物的锁车方式是从正确密码开始,每次随机转动密码锁一次,可以单独转动一个拨圈,或者同时转动两个相邻的拨圈,但两个拨圈的转动幅度必须相同。他记录了锁车后密码锁的多个状态,这些状态都不是正确密码。现在需要计算有多少种可能的正确密码,使得这些密码通过这个神秘人物的锁车方式能够产生所有记录的状态。
思路
对于第 \(i\) 个密码锁状态,只需两个 for 循环模拟旋转,一个模拟转 \(1\) 个拨圈,一个模拟转 \(2\) 个拨圈,之后再把这个状态用 compress 压缩一下(方便处理),然后丢掉一个集合 \(S_i\) 中。最后将所有集合求交集就是答案个数,即 \(S_1 \cap S_2 \cap \cdots \cap S_n\) 的大小。
代码
//此处省略八个字或一串 base64 代码,具体是什么你自己认为是啥就是啥吧。
#include<bits/stdc++.h>
using namespace std;
inline int compress(vector<int> a)
{
int ret=0;
for(int i=1;i<=5;i++) ret=ret*10+a[i];
return ret;
}
int main()
{
freopen("lock.in","r",stdin);
freopen("lock.out","w",stdout);
int n;
cin>>n;
set<int> ss[10];
for(int T=1;T<=n;T++)
{
vector<int> a;
a.resize(8);
cin>>a[1]>>a[2]>>a[3]>>a[4]>>a[5];
vector<int> b;
// int cnt0=0,cnt1=0,tmp=0;
for(int i=1;i<=5;i++)
{
// tmp=s.size();
b=a;
for(int j=0;j<=9;j++)
{
if(a[i]==j) continue;
b[i]=j;
ss[T].insert(compress(b));
}
// cnt0+=s.size()-tmp;
// tmp=s.size();
b=a;
for(int j=1;j<=9;j++)
{
if(i==5) continue;
int b11=b[i],b111=b[i+1];
b[i]=(b[i]+j)%10,b[i+1]=(b[i+1]+j)%10;
ss[T].insert(compress(b));
b[i]=b11,b[i+1]=b111;
}
}
}
unsigned long long toto=0;
for(auto i:ss[1])
{
bool flag=true;
for(int j=2;j<=n;j++)
{
if(ss[j].find(i)==ss[j].end())
{
flag=false;
break;
}
}
if(flag) toto++;
}
cout<<toto;
return 0;
}
(2024·提高·T1) 决斗
思路
先从 \(r_i \le 2\) 入手,容易发现要使剩下的怪兽最少,必须要让每个 \(r=2\) 的怪物杀死一个 \(r=1\) 的怪物。
试着将结论推广到 \(r \le 10^5\) 的情况,只需要让一只怪兽杀死一只防御力和自己攻击力最接近且比自己攻击力小的怪物。比如对于以下怪兽:
\({\color{red}6,6},{\color{blue}5},{\color{green}4,4},{\color{brown}3},{\color{purple}1}\)
可以进行以下操作:
-
让一只 \(r=3\) 的怪兽杀一只 \(r=1\) 的怪兽:\({\color{red}6,6},{\color{blue}5},{\color{green}4,4},{\color{brown}3},{\color{purple}\xcancel{1}}\)
-
让一只 \(r=4\) 的怪兽杀一只 \(r=3\) 的怪兽:\({\color{red}6,6},{\color{blue}5},{\color{green}4,4},{\color{brown}\xcancel{3}},{\color{purple}\xcancel{1}}\)
-
让一只 \(r=5\) 的怪兽杀一只 \(r=4\) 的怪兽:\({\color{red}6,6},{\color{blue}5},{\color{green}4,\xcancel{4}},{\color{brown}\xcancel{3}},{\color{purple}\xcancel{1}}\)
-
让两只 \(r=6\) 的怪兽杀一只 \(r=4\) 和一只 \(r=5\) 的怪兽:\({\color{red}6,6},{\color{blue}\xcancel{5}},{\color{green}\xcancel{4},\xcancel{4}},{\color{brown}\xcancel{3}},{\color{purple}\xcancel{1}}\)
对于 \(r=1\) 的怪兽,只需要让它挠一下 \(r \ge 1\) 的怪兽即可。因为敌方防御力大于等于自己攻击力,所以本次攻击无事发生。
我们只需要建立两个小根堆(即优先队列,C++ 中的 priority_queue)维护一个杀手队列和一个猎物队列,将每个 \(r\) 加入,当杀手队列非空的时候进行如下操作:
- 如果当前杀手、猎物队列队首元素 \(k_1,m_1\) 满足 \(k_1>m_1\),即当前杀手攻击力大于猎物防御力时,说明杀手可以杀死猎物,弹出杀手和猎物队列的首元素。
- 否则,说明杀手杀不死猎物,只需弹出杀手队列的首元素即可。
时间复杂度 \(O(n \log n)\),足以通过本题。
代码
//I'm Neuvillette and Alhaitham's ___
//A. 厨 B. 推 C. 激推 D.
//这道题应该不是选“apple”也不是选“boy”吧。为什么有一个空白的选项呢?并非空白。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e5+7;
int a[N];
priority_queue<int,vector<int>,greater<int>> killer,mob;
//杀手和猎物
int main()
{
freopen("duel.in","r",stdin);
freopen("duel.out","w",stdout);
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
{
killer.push(a[i]);
mob.push(a[i]);
}
while(!killer.empty())
{
int k1=killer.top();killer.pop();
int m1=mob.top();
if(k1>m1) mob.pop();
}
cout<<mob.size();
return 0;
}
/*
没错,以下内容来自于某人语文可能写错的诗句,写在上面了,绝无特殊含义。
这个十六进制数字也是一个毫无特殊含义的数字。和诗句中对应的第几个字无关。
(12AA33)₁₆
我寄愁心与明月,随君直到夜郎西。 ——李白《闻王昌龄左迁龙标遥有此寄》
以是人多以书假余,余因得遍观群书。——宋濂《送东阳马生序》
枯藤老树昏鸦,小桥流水人家。——马致远《天净沙·秋思》
故园东望路漫漫,双袖龙钟泪不干。——岑参《逢入京使》
马作的卢飞快,弓如霹雳弦惊。——辛弃疾《破阵子·为陈同甫赋壮词以寄之》
兔从狗窦入,雉从梁上飞。——《乐府诗集》
*/
(2024·提高·T2) 超速检测
题目虽然不毒瘤,但是细节非常多。写了三个中午还多(3.5h)才写完。
题目
给定一条长为 \(L\) 的主干道,上面有 \(n\) 辆车和 \(m\) 个测速仪。每辆车从某个位置 \(d_i\),进入主干道,以初速度 \(v_i\) 和加速度 \(a_i\) 向北行驶,第 \(j(1 \le j \le m)\) 个测速仪位于 \(p_j\) 的位置,当车辆经过某个开启的测速仪时,如果速度超过限速 \(v_{\lim}\) 则判定为超速。
现要求两个问题:当所有测速仪都开启时,有多少辆车会被判定为超速;以及在不漏掉任何超速车辆的前提下,最多可以关闭多少个测速仪。
思路
观察题目发现:所有车辆可以分为三种:匀速直线运动、匀加速直线运动、匀减速直线运动。
考场思路:
首先特殊性质 A,所有车都匀速直线运动,显然是最好处理的,直接 \(O(n)\) 扫一遍,第一问可以求出来。对于第二问,显然每辆车的行驶范围都在 \([d_i,L]\),不存在中途离开车道的情况。所以如果有车超速就开一个测速仪干掉这辆车,没有车超速就全都关闭。
对于特殊性质 B,所有车都匀加速直线运动,同样没有车中途离开道路,那么只需要判断在最后一个测速仪是否超速就可以了。即当车的位移 \(\Delta x=p_m-d_i\) 时,若速度 \(v' = \sqrt{v_{初}^2+2a\Delta x} \le v_{\lim}\) 即没有超速。对于第二问,同特殊性质 A,测速仪要么全部关闭要么都打开。
对于测试点 \(1,2\),直接先 \(O(nm)\) 处理第一问,两重 for 循环判断第 \(i(1 \le i \le n)\) 辆车有没有在第 \(j(1 \le j \le m)\) 处超速;对于第二问,dfs 枚举每个测速仪开没开就可以了。时间复杂度 \(O(nm+2^m)\)。于是恭喜你拿到了 \(50\) 分。
对于 \(100 \%\) 的数据,显然这种方式是行不通的。于是看到特殊性质 ABC 已经分好了类:匀速直线运动、匀加速直线运动、匀减速直线运动(分别对应特殊性质 A、B、C)。画个图可以发现,每辆车都有一个超速区间(记为 \(S\)),分情况讨论:
A. 匀速直线运动
- 若刚开始就超速,此时 \(v_i > v_{\lim}\),\(S=[d_i,L]\);
- 若一直都不超速,此时 \(v_i \le v_{\lim}\),\(S=\varnothing\).
B. 匀加速直线运动
- 若刚开始就超速,此时 \(v_i > v_{\lim}\),\(S=[d_i,L]\);
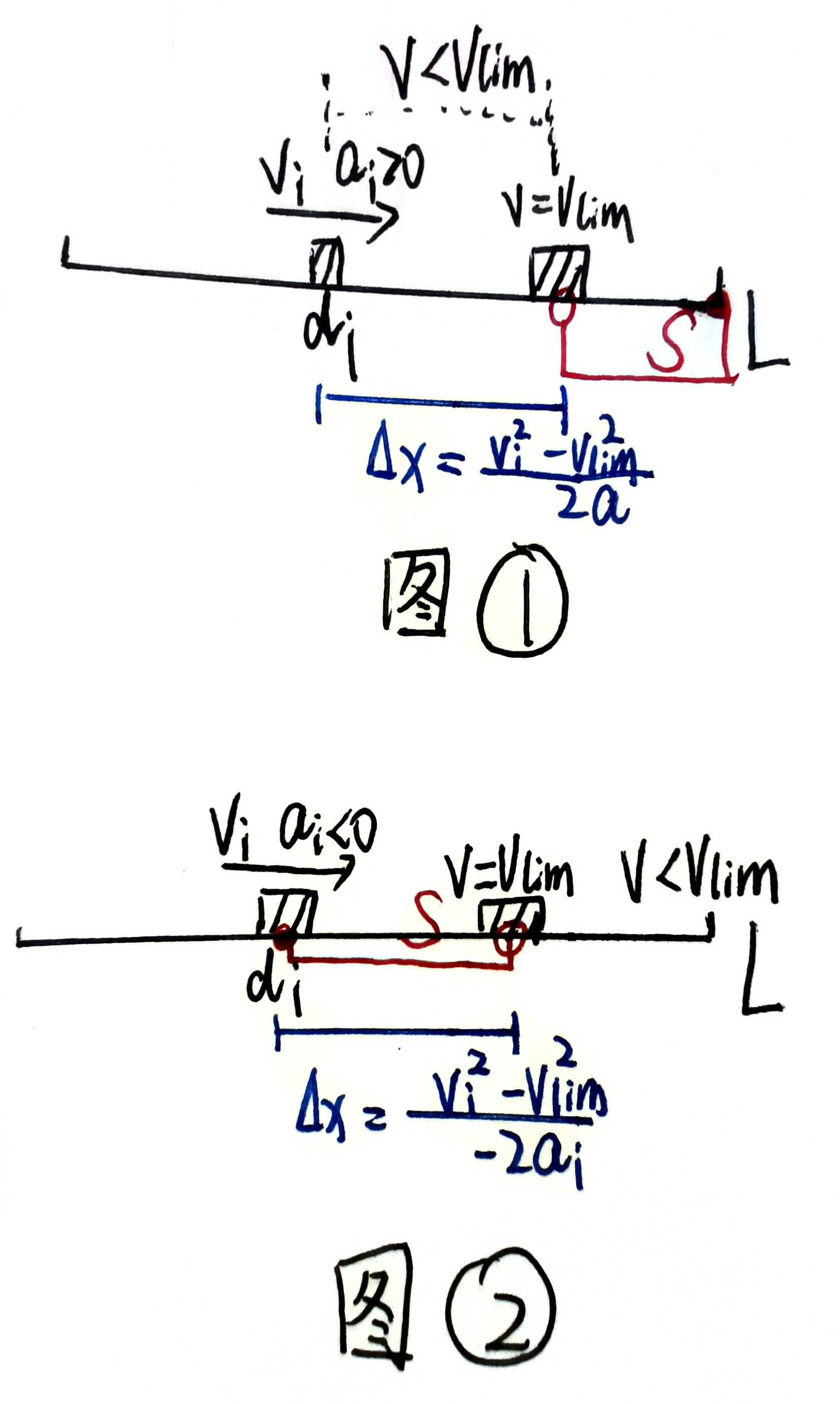
- 若刚开始没有超速,则车辆的速度一定会在行驶一段时间后超过 \(v_{\lim}\),由运动学规律 \(v^2-v_0^2=2ax\) 知:当车辆在位移 \(\Delta x=\dfrac{v_i^2-v_{\lim}^2}{2a}\) 后开始持续超速。此时车辆已经行驶到 \(d_i+\dfrac{v_i^2-v_{\lim}^2}{2a}\),\(S=(d_i+\dfrac{v_i^2-v_{\lim}^2}{2a},L]\)(注意区间的开闭)(具体图示可参考图①)
C. 匀减速直线运动
- 若刚开始已经超速,则会在行驶 \(\Delta x=\left| \dfrac{v_i^2-v_{\lim}^2}{2a_i} \right|=\dfrac{v_i^2-v_{\lim}^2}{-2a_i}\) (推导过程同上)后速度下降至 \(v_{\lim}\),停止超速。\(S=\dfrac{v_i^2-v_{\lim}^2}{-2a_i}\).(注意 \(a_i < 0\) 所以去掉绝对值的时候要注意把负号加上)(具体图示可参考图②)
- 若刚开始没有超速,因为速度越来越小直到为 \(0\),所以这辆车不会超速。\(S=\varnothing\).
对于第一问,在处理超速区间问题时,判断如果车辆超速且能被测速仪看到,那就将这辆车丢到一个桶里(方便第二问),答案就为该桶所含元素的个数。
对于第二问,为了方便求解,可以将超速区间 \(S\) 转化成测速仪区间的形式,即“车辆在 \([s,t]\) 处超速行驶”转化成“车辆超速行驶,且能被编号为 \([s',t']\) 的测速仪检测”。具体可在主函数预处理两个记录距离 \(x\) 处最近的且位于 \(x\) 左/右边的测速仪编号的数组 \(lt_x,rt_x (1 \le i \le \textbf{L})\)(注意数组大小不要开到 \(n\) 或 \(m\) 去了),然后记录超速区间 \([s,t]\) 时直接记录 \([rt_s,lt_t]\) 就可以了。
现在第二问转化为:对于若干个区间 \([s',t']\),要求选择若干个点,使得每个区间都包含一个点(即对于每个超速区间都有一个测速仪可以检测得到)。这是一个很经典的贪心问题(洛谷 P1250 种树):
路边的地区被分割成块,并被编号成 \(1, 2, \ldots,n\)。每个部分为一个单位尺寸大小并最多可种一棵树。
每个居民都想在门前种些树,并指定了三个号码 \(b\),\(e\),\(t\)。这三个数表示该居民想在地区 \(b\) 和 \(e\) 之间(包括 \(b\) 和 \(e\))种至少 \(t\) 棵树。
居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量。
只需按照右端点从小到大排序,接着从左边开始遍历每一个测速仪的位置并记录 id(最开始设置成 \(0\) 或者像我代码一样设置成 -12181222 该数字与某两个角色的生日无任何关系),如果当前测速仪管不到超速的车辆了(车的超速区间为 \([s',t']\),\(s>id\) 即最后一个开的测速仪还在这辆车的超速区间前),就在右端点新开一个测速仪。最后第二问的答案就是用总测速仪个数 \(m\) 减去开着的测速仪个数就可以了。
代码
//我猜你在等一个一字主语+一字谓语+五字定语+一字宾语的句子,对吧
//你知道我要写什么的
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e5+7;
constexpr int M=1e5+7;
constexpr int L=1e6+7;
constexpr double eps=1e-5;
int csl[N],csr[N]; //第i个车的(测速仪能管到的)超速区间
int d[N],v[N],a[N],p[N];
int n,m,len,vlim;
vector<int> cs; //超速车辆
int lt[L],rt[L]; //lt/rt[i]表示距离i最近且位于i左/右侧的测速仪的编号
void R(int id,int lll,int rrr) //修改区间(Range)
{
csl[id]=lll;
csr[id]=rrr;
}
inline void getrange(int i)
{
if(d[i]>p[m]) return;
if(a[i]==0) //匀速直线运动
{
if(v[i]>vlim)
{
R(i,rt[d[i]],m); //超速了就全程都超速
cs.push_back(i);
}
}
if(a[i]>0) //匀加速直线运动
{
if(v[i]>vlim)
{
R(i,rt[d[i]],m); //开局就超速
cs.push_back(i);
}
else
{
int deltax=(vlim*vlim-v[i]*v[i]); //位移(记得分数要写括号)
deltax=deltax/(2*a[i]);
int start=d[i]+deltax+1;
//开始超速的位置(di+位移),注意要变成比start大一点的整数(因为是左开区间)
//结束超速的位置是L
// if(start<0) cerr<<start<<endl;
if(start<=p[m]) //可以被测速仪发现
{
cs.push_back(i); //登记为超速车辆
R(i,rt[start],m);
}
}
}
if(a[i]<0) //匀减速直线运动
{
//v[i]<=vlim就一直都没有超速
if(v[i]>vlim)
{
//注意右开区间处理:要变成一个稍微小点的整数
int deltax=(v[i]*v[i]-vlim*vlim);
int stopp;
if(deltax%(-2*a[i])==0) stopp=d[i]+deltax/(-2*a[i])-1;
else stopp=d[i]+deltax/(-2*a[i]);
// cerr<<i<<":"<<stopp<<endl;
//超速结尾在最后一个测速仪后
if(stopp>=p[m])
{
cs.push_back(i);
R(i,rt[d[i]],m);
}
else
{
assert(stopp>=0);
R(i,rt[d[i]],lt[stopp]);
if(csr[i]>=csl[i]) cs.push_back(i);
}
}
}
// fprintf(stderr,"i=%d [%d,%d]\n",i,p[csl[i]],p[csr[i]]);
}
inline int solve2() //贪心
{
int cnt=0;
sort(cs.begin(),cs.end(),[&](int A,int B)
{
return csr[A]<csr[B];
});
int id=-12180211; //当前开到第几个测速仪
// cerr<<"超速车辆:";
// for(int i:cs) cerr<<i<<" ";
// cerr<<"\n";
for(int i:cs)
{
// cerr<<"The velocity limit exceed range of car"<<i<<"is "<<csl<<' '<<csr<<endl;
if(csl[i]>id) //测速仪管不到了
{
id=csr[i]; //在右边开一个测速仪
cnt++;
// cerr<<"need a new tester on car "<<i<<"\n";
}
// cerr<<"now tester "<<id<<", total="<<cnt<<"\n";
}
return m-cnt;
}
int main()
{
freopen("detect.in","r",stdin);
freopen("detect.out","w",stdout);
int T; //多测不清空,爆零两行泪
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d%d",&n,&m,&len,&vlim);
for(int i=1;i<=n;i++) scanf("%d%d%d",&d[i],&v[i],&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&p[i]);
p[0]=0,p[m+1]=len+1;
for(int i=1;i<=m;i++) lt[p[i]]=rt[p[i]]=i;
//更新lt,rt数组
cs.clear();
for(int i=0;i<=m;i++)
for(int j=p[i]+1;j<p[i+1];j++)
lt[j]=i,rt[j]=i+1;
for(int i=1;i<=n;i++) getrange(i);
printf("%d %d\n",(int)cs.size(),solve2());
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号