数据结构期末树

树

基本概念

1.最多一个先驱但可能有多个后继表示具有层次的分支关系

2.Siblings（兄弟）: nodes share the same parent

Degree(树的扇出) of a tree: the maximum number of its node.

3.深度为最大层数

第i层最多2^i个结点

4.完全二叉树：满二叉树去掉最下面一层最右边若干节点

完全二叉树深度 log2(n)向下取整

第i个结点左孩子2i+1 右孩子2i+2

父结点(i-1)/2

5.preorder(TreeNode * root){

if(root!=NULL){

cout<<root->val<<endl;

preorder(root->left);

preorder(root->right);}

inorder(TreeNode * root){

if(root!=NULL){

inorder(root->left);

cout<<root->value<<endl;

inorder(root->right);}

postorder

6.完全二叉树的数组存储

孩子与父亲节点的关系父亲i 左孩子2i+1 右孩子2i+2

7.完全二叉树插入、删除(3种情况)、查找、利用二叉查找树排序

插入

在二叉树末尾插入只需要知道二叉树父节点的信息即父节点的指针

当前插入节点temp=size();

判断是左节点还是右节点；将信息入栈

求出父节点的索引；

判断父节点是否为根节点，若不是重复上述操作；

查找到根节点后栈内保存从根节点到插入节点的信息，获取父节点指针；

将当前信息插入树中；

二叉搜索树

tree search

递归
TreeNode *search_for_node(TreeNode * root,int &target){
if(root==NULL||root->val==target) return root;
else if(target>root->val) return search_for_node(root->right,target);
else  return search_for_node(root->left,target);
}
非递归
TreeNode *search_for_node(TreeNode * root,int &target){
while(root!=NULL&&root->val!=target)
{
if(root->val>target) root=root->right;
else root=root->left;}
return root;}
template <class Record>
Error_code Search_tree<Record> :: tree_search(Record &target) const
{
    Error_code result = success;
    Binary_node<Record> *found = search_for_node(root, target);
    if (found == NULL)
        result = not_present;
    else
        target = found->data;
    return result;
}

二叉查找树insert

template <class Record>
Error_code Search_tree<Record> :: insert(
                                             const Record &new_data)
{//插入成功返回 success
  //插入失败返回 duplicate_error
    Error_code result=search_and_insert(root, new_data);
    if(result==success)count++;
    return result;
}
template <class Record>
Error_code Search_tree<Record> :: search_and_insert(
                       Binary_node<Record> * &sub_root , 
                       const Record &new_data)
{if(sub_root==NULL) {sub_root=new Binary_node<Record>(new_data) ;
return success;}
else if(new_data>sub_root->val) return search_and_insert(sub_root->right,new_data);
else if(new_data<sub_root->val) return search_and_insert(sub_root->left,new_data);
else return duplicate_error;}

二叉查找树中序遍历即为有序序列

适用于无序序列对基本有序序列排序效率较低（较不平衡

二叉查找树的删除

1）删除节点为叶子节点左右子树均为空

2）删除节点左右子树有一个非空 子树根节点与删除节点的父亲相连

3）删除节点左右子树均非空

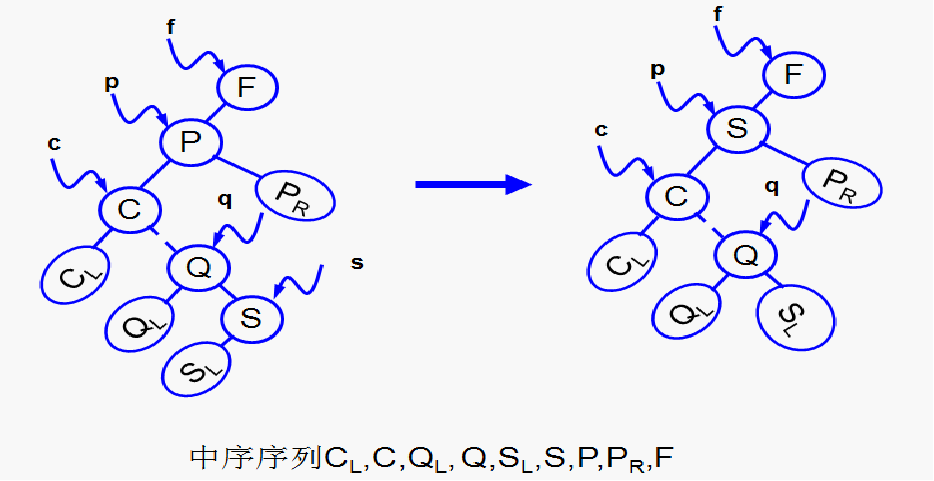
找到被删除节点中序遍历的前驱用前驱代替被删除点

template <class Record>
Error_code Search_tree<Record> :: remove(const Record &target)
/* Post: If a Record with a key matching that of target belongs to the Search tree a code of success is returned and the corresponding node is removed from the
tree. Otherwise, a code of not present is returned.
Uses: Function search_and_destroy */
{
    Error_code result=search_and_destroy(root, target);
    if(result==success)count--;
    return result;
}
Error_code Search_tree<Record> :: search_and_destroy(
                                                           Binary_node<Record>* &sub_root,                     
                                                           const Record &target)
{if(sub_root==NULL||sub_root->val==target)
return remove_root(sub_root);
else if(sub_root->val>target) return search_and_destroy(root->right);
return search_and_destroy(root->left);}
template <class Record>
Error_code Search_tree<Record> :: remove_root(Binary_node<Record> * &sub_root)
{if(sub_root==NULL) return not_present;
Binary_node<Record> *to_delete=sub_root;
else if(sub_root->right!=NULL) sub_root=sub_root->right);
else if(sub_root->left!=NULL) sub_root=sub_root->left;
else{
to_delete=sub_root->left;
Binary_node<Record> * parent=sub_root;
while(to_delete->right!=NULL){
parent=to_delete;
to_delete=to_delete->right;}
if(parent==sub_root)sub_root->left=to_delete->left;
else parent->right=to_delete->left;}

delete to_delete; // Remove to_delete from tree.

return success; }

8.堆

1）完全二叉树的存储用数组存

2）堆和完全二叉树对应

3）堆的定义大顶堆父亲比孩子大的完全二叉树

4）堆的调整先决条件左右孩子都是堆

固定操作取max 调整堆

5）Build-Heap(A) for i from n/2 downto 1 do Heapify(A, i)

从第一个非叶子节点开始从后往前依次进行对调整

6）堆排序空间复杂度O(1) 因为将堆顶取出将取出的数放到数组尾部从后往前堆不断变小从第一个非叶子节点从后往前一次调整成堆通过调整操作建成堆

第一步构造初始堆将给定无序序列构造成大顶堆（一般降序用小顶堆升序用大顶堆）

第二步将堆顶元素与末尾元素交换使数组末尾元素最大

然后调整堆再将堆顶元素和末尾元素交换如此反复操作

思路总结

　 a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

时间复杂度 O(nlogn)

它的最坏，最好，平均时间复杂度均为O(nlogn)

7）结合完全二叉树存储堆排序在数组中怎么变

8）Topk算法 //往堆上想

若要时刻输出最大的K个数维护一个小顶堆每次弹出堆中最小的元素保证堆内元素是最大的K 个

时间复杂度O(klogk)

9.AVL树

如何判断是否是一颗AVL树

先判断该树中序遍历后是否有序

在判断是否平衡

10.Trie树

Tries 应用字符串匹配的相关算法，如前缀匹配-type ahead

11.树上基本的递归操作节点的存储

https://juejin.im/post/5b3b55c2e51d45195d7d8c20

最大深度

int depth(TreeNode * root)
{
if(root==NULL)return 0;
return 1+max(depth(root->left),depth(root->right));}

111二叉树的最小深度

 int minDepth(TreeNode* root) {
        if(root==NULL)return 0;
        if(root->left==NULL&&root->right==NULL)return 1;
        if(root->left==NULL&&root->right!=NULL)return  minDepth(root->right)+1;
        if(root->right==NULL&&root->left!=NULL)return minDepth(root->left)+1;
        return min(minDepth(root->left),minDepth(root->right))+1;
    }

226翻转二叉树

TreeNode* invertTree(TreeNode* root) {
        if(root==NULL)return NULL;
        swap(root->left,root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }

110平衡二叉树

 bool isBalanced(TreeNode * root){
if(root==NULL)return true;
if(abs(depth(root->left)-depth(root->right))>1)
return false;
return isBalanced(root->left)&&isBalanced(root->right);}

100相同的树

 bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p==NULL&&q==NULL)return true;
        if(p==NULL&&q!=NULL)return false;
        if(p!=NULL&&q==NULL)return false;
        if(p->val!=q->val)return false;
        return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
    }

101对称二叉树

 bool isSymmetric(TreeNode* root) {
        if(root==NULL)return true;
        return ismirror(root->left,root->right);
    }
    bool ismirror(TreeNode * p,TreeNode * q)
    {
        if(p==NULL&&q==NULL)return true;
        if(p!=NULL&&q==NULL)return false;
        if(p==NULL&&q!=NULL)return false;
        if(p->val!=q->val)return false;
        return ismirror(p->left,q->right)&&ismirror(p->right,q->left);
    }

222完全二叉树结点个数

  int countNodes(TreeNode* root) {
        if(root==NULL)return 0;
        return countNodes(root->left)+countNodes(root->right)+1;
    }

112路径总和

 bool hasPathSum(TreeNode* root, int sum) {
        if(root==NULL)return false;
        if(root->left==NULL&&root->right==NULL)return root->val==sum;
        return hasPathSum(root->left,sum-root->val)||hasPathSum(root->right,sum-root->val);
    }

257二叉树的所有路径

 vector<string> binaryTreePaths(TreeNode* root) {
        if(root==NULL)return res;
        binary(root,res,"");
        return res;
    }
    void binary(TreeNode * root,vector<string>&res,string path)
    {
        if(root==NULL)return;
        path+=to_string(root->val);
        if(root->left==NULL&&root->right==NULL)
        res.push_back(path);
        if(root->left!=NULL)binary(root->left,res,path+"->");
        if(root->right!=NULL)binary(root->right,res,path+"->");
    }

129求根到叶子节点数之和

int result=0;
int temp=0;
    int sumNumbers(TreeNode* root) {
     dfs(root);
     return result;
    }
    void dfs(TreeNode * root)
    {
        if(root==NULL)return ;
        temp=10*temp+root->val;
        if(root->left==NULL&&root->right==NULL)
        result+=temp;
        if(root->left)
        {dfs(root->left);
        temp/=10;
        }
        if(root->right)
         {dfs(root->right);
        temp/=10;
        }
    }

437路径总和3

int pathSum(TreeNode* root, int sum) {
        if(root==NULL)return 0;
       return path(root,sum)+pathSum(root->left,sum)+pathSum(root->right,sum);
    }
    int path(TreeNode * root,int sum)
    {
        if(root==NULL)return 0;
        return (root->val==sum)+path(root->left,sum-root->val)+path(root->right,sum-root->val);
    }

二叉树最大路径和

  int maxPathSum(TreeNode* root) {
        if(root==NULL)return 0;
        int result=-1000;
      maxPath(root,result);
return result;
    }
    int maxPath(TreeNode * root,int &val)
    {
        if(root==NULL)return 0;
        int left=max(0,maxPath(root->left,val));
        int right=max(0,maxPath(root->right,val));
        int ret=root->val+max(left,right);
        int lar=root->val+left+right;
        val=max(val,max(lar,ret));
        return ret;
    }

113路径总和2

vector<vector<int>>result;
vector<int>path;
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        if(root==NULL)return result;
       hasPath(root,sum,result,path);
       return result;
    }
    void hasPath(TreeNode * root,int sum,vector<vector<int>>&result,vector<int>&path)
    {path.push_back(root->val);
        if(root->left==NULL&&root->right==NULL&&root->val==sum)
       {result.push_back(path);
        return;} 
        
        if(root->left!=NULL)
        {
           hasPath(root->left,sum-root->val,result,path);
           path.pop_back();
        }
         if(root->right!=NULL)
        {
           hasPath(root->right,sum-root->val,result,path);
           path.pop_back();
        }
    }

posted @ 2019-12-29 21:28 柠檬味呀阅读(291) 评论(0) 收藏举报

刷新页面返回顶部

柠檬味呀

数据结构期末 树

公告

数据结构期末树