TQX DP again

AGC035D Add and Remove

感觉有点像Pocky Game的套路。

显然最后只会剩下 $a_1$ 和 $a_n$，我们不考虑这两个数。

一开始会想到设 $f_{l,r}$ 表示区间 $[l,r]$ 在 $a_{l-1},a_{r+1}$ 之前删除的答案，你会发现它无法考虑到 $a_{l-1},a_{r+1}$ 的影响，于是我们将这两个值也计入状态。令 $f_{l,r,fl,fr}$ 表示删除区间 $[l,r]$ 时，$a_{l-1}$ 被计算了 $fl$ 次，$a_{r+1}$ 被计算了 $fr$ 次的贡献，转移枚举间断点计算即可。

$(fl,fr)$ 的变化可以看成一棵二叉树，总状态数是 $\Theta(n^22^n)$ 的。

CF1517F Reunion

设有空的志愿者是黑点，没空的是白点。

考虑枚举半径 $r$，计数恰好 $r$ 的转化成计数 $\le r$。容易发现条件等价于任意一个黑点 $r$ 步之内必有白点，即所有白点拓展 $r$ 步覆盖了所有黑点。

容易想到设 $f_{i,j,k}$ 表示点 $i$ 子树内最浅的白点深度为 $j$，未被覆盖的黑点深度最深为 $k$ 的方案数，直接转移是 $O(n^4)$ 的。我们发现所有黑点都被覆盖就不用记录 $j$，否则这个子树内的白点没有用的。我们将 $j/k$ 压到一维，用正负表示有用的是 $j$ 还是 $k$，树上背包即可变成 $O(n^2)$

P7897 [Ynoi2006] spxmcq

设 $f_i$ 表示以 $i$ 为根的答案，那么暴力 dp 是显然的：$f_i=a_i+x+\sum \max\left(f_v,0\right)$

$\max$ 很讨厌，我们考虑维护一个森林，$i\rightarrow fa_{i}$ 有边当且仅当 $f_i>0$，显然这个森林随着 $x$ 的增大只会加边。我们离线按 $x$ 排序，每次找出要加的边，树状数组维护子树和即可。问题变为如何快速找到要加的边。

设 $siz$ 为子树大小，$sum$ 为子树和，那么 $f_i=sum_i+xsiz_i$，$f_i>0$ 的条件是 $x\ge \lceil{-sum_i\over siz_i}\rceil$，维护一个小根堆，按 $\lceil{-sum_i\over siz_i}\rceil$ 排序即可。容易发现链一条边至多只会影响一个点的值。

CF1326G Spiderweb Trees

咕咕咕

CF1456E XOR-ranges

我们考虑对于 $x_i$，它在哪一位能解除 $[l_i,r_i]$ 的限制。我们发现 $l_i,r_i$ 首先往上有若干位是相同的；对于第一个不同的位置，它可以选择解除上界/下界的限制；对于接下来的位置，可以在一个 $1$ 处解除上界/在一个 $0$ 处解除下界。如果一个 $x$ 在之后没有限制了，那么它的最优方案显然是和左边/右边的数选的一样，相当于它已经不存在了，我们将它删去不影响结果。

于是考虑设 $f_{c,l,r,0/1,0/1,0/1,0/1}$ 表示 考虑到从高到低第 $c$ 位，$l,r$ 被删完了，并且 $l-1$, $r+1$ 没有被删去，确定了 $l-1$,$r+1$ 的限制情况。考虑倒着转移，枚举哪个数脱离了限制即可，注意可以没有数解除限制。

CF1158F Density of subarrays

脑车题。

考虑算一个序列的密度：每个位置向所有它之后 $[1,c]$ 中每个数第一次出现的位置连边，密度就是从头走到尾的最短路，显然可以每次贪心的往后面走

然后有个显然的 dp：设 $f_{i,j}$ 表示考虑到前 $i$ 个位置，第 $i$ 个位置被选择且在最短路上，最短路长度为 $j$ 的方案，显然你可以枚举上一个位置在哪里，转移系数是在这个区间里选一个密度为 $1$ 的子序列的方案数，这个显然是 $\prod (2^{cnt_i}-1)$(强制 $cnt_{a_{i-1}}=1$)。可以 $O(n^2)$ 预处理。

稍加分析你会发现密度不超过 $n\over c$，转移是 $\Theta\left({n^3\over c}\right)$ 的。

你发现在 $c$ 很小的时候它挂了，但是在 $c$ 很小的时候你可以直接状压元素的出现状态，得到一个 $\Theta\left({n^22^c\over c}\right)$ 的 dp。

综合两个做法就可以过了。

CF1466H Finding satisfactory solutions

$i$ 向 $a_i$ 连黑边，如果 $i$ 更喜欢 $j$，那就向 $j$ 连白边，合法等价于没有白边在一个环上。

于是把黑边连的环缩起来，相当于计数连出一个 DAG 的方案数，有一个套路的状压+容斥做法。

我们发现大小相同的环没有本质区别，把状压的东西改成所有不同大小的环的数量，状态变成了 $n$ 的拆分数的级别，可以通过。

P3642 [APIO2016] 烟火表演

$f_i(x)$ 表示 $i$ 子树内到 $i$ 的时间为 $x$ 的最小代价，转移时显然的。

容易发现它是若干个下凸函数相加，自然也是个下凸函数，考虑 Slope Trick，考虑将它加到父亲节点的影响，分四段讨论即可。

考虑 $f_i(0)$ 直接就是边权和，所以答案可以通过 $f_i(0)$ 简单推出。

P4655 [CEOI2017] Building Bridges

写出暴力 dp 式子，发现后面的转移是个一次函数，李超树优化即可。

CF1603D Artistic Partition

有一个显然的 2d/1d dp，推推式子发现满足四边形不等式，分治即可。

AGC035E Develop

$x$ 向 $x-2$ 和 $x-K$ 连边，显然我们最后删掉的点集中不可能有环。观察一下环长什么样，不难想到分奇偶讨论：

如果 $K$ 是偶数，显然奇偶性相同的是两个连通块，对两个分开考虑。我们发现没有环的限制可以被表述成不能选连续的 $K\over 2$ 个数，简单 dp 即可。

如果 $K$ 是奇数，考虑下图：

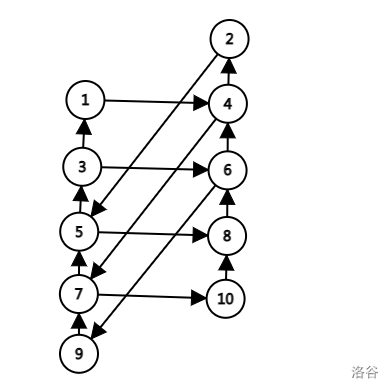
每个环一定是形如向上向右在向上然后找到一个能连下来的节点，我们考虑从上往下逐层 dp，设 $f_{i,j,k}$ 表示考虑到第 $i$ 层，最长的向上向右在向上的路径长为 $j$ 且 图右边从 $i$ 曾向上连续 $k$ 个点都被选中了的方案数，转移考虑这一层两个节点的 $4$ 种选择情况即可。

CF1292F Nora's Toy Boxes

咕咕咕