算法基础(二):递归
递归
一个函数调用其自身,就是递归。递归和普通函数调用一样是通过栈实现的。
汉诺塔问题
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
#include<iostream>
using namespace std;
void Hanoi(int n,char src,char mid,char des t,int src_n)
//将src座上的n个盘子,以mid为中转,移动到dest座
//src座上最上方盘子编号是src_n
{
if(n==1){ //只需移动一个盘子
cout<< src_n<<":"<<src<<"->"<<dest<<endl;
//直接将盘子从src移动到dest即可
return ;
}
Hanoi(n-1,src,dest,mid,src_n);//先将n-1个盘子从src移动到mid
cout<<src_n+n-1<<":"<<src<<"->"<<dest<<endl;
//再将一个盘子从src移动到dest
Hanoi(n-1,mid,src,dest,src_n); //最后将n-1ge盘子从mid移动到dest
return;
}
int main()
{
char a,b,c;
int n;
cin>>n>>a>>b>>c;//输入盘子数目
Hanoi(n,a,b,c,1);
return 0;
递归的作用
1.替代多重循环
2.解决本来就是用递归形式定义的问题
3.将问题分解为规模更小的子问题进行求解
......
n皇后问题
输入整数n,要求n个国际象棋的皇后,摆在n*n的棋盘上,互相不能攻击,输出全部方案。(n是变量)
递归替换循环!
输入:N
输出:每一行都代表一种摆法。第i个数字为n代表第i行的皇后应该放在第n列。(行列都从1开始算)
#include<iostream>
#include<cmath>
using namespace std;
int N;
int queenPos[100];//用来存放算好的皇后位置。最左上角是(0,0)
void NQueen(int k);
int main()
{
cin>>N;
NQueen(0);//从第0行开始摆皇后
return 0;
}
void Nqueen(int k)//在0~k-1行皇后已经摆好的情况下,摆第k行及其后的皇后
{
int i;
if(k ==N){//N个皇后已经摆好
for(int i=0;i<N;i++)
cout<<queenPos[i]+1<<" ";
cout<<endl;
return;
}
for(int i=0;i<N;i++){//逐个尝试第k个皇后的位置
int j;
for(j=0;j<k;j++){
//和已摆好的k个皇后比较看是否冲突
if(queenPos[j]==i|| abs(queenPos[j]-i)==abs(k-j)){
break;
}
}
if(j==k){ //当前选的位置i不冲突
queenPos[k]=i;//将第k个皇后摆放在i
Nqueen(k+1);
}
}
}
逆波兰表达式(前置)
逆波兰表达式是一种把运算符前置的算术表达式(有些教材上称为波兰表达式),其优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2+3)4的逆波兰表达式为 + 2 3 4.
输入:输入为一行,其中运算符和运算数之间都用空格分隔,运算数是浮点数。
输出:表达式的值
思路关键:
1.一个数看成一个表达式,值为该数
2.”运算符+表达式+表达式“=表达式,值为两个表达式运算的结果
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
double exp(){
//读入一个逆波兰表达式,并计算其值
char s[20];
cin>>s;
switch (s[0]){
case '+': return exp()+exp();
case '-': return exp()-exp();
case '*': return exp()*exp();
case '/': return exp()/exp();
default: return atof(s);
break;
}
}
int main(){
printf("%lf",exp());
return 0;
四则运算表达式求值
输入为四则运算表达式,仅由整数、+、-、*、/、(、)组成,无空格,要求求其值。假设运算符结果都是整数。 “/”结果也是整数
表达式是一个递归的定义!!循环定义 的表达式
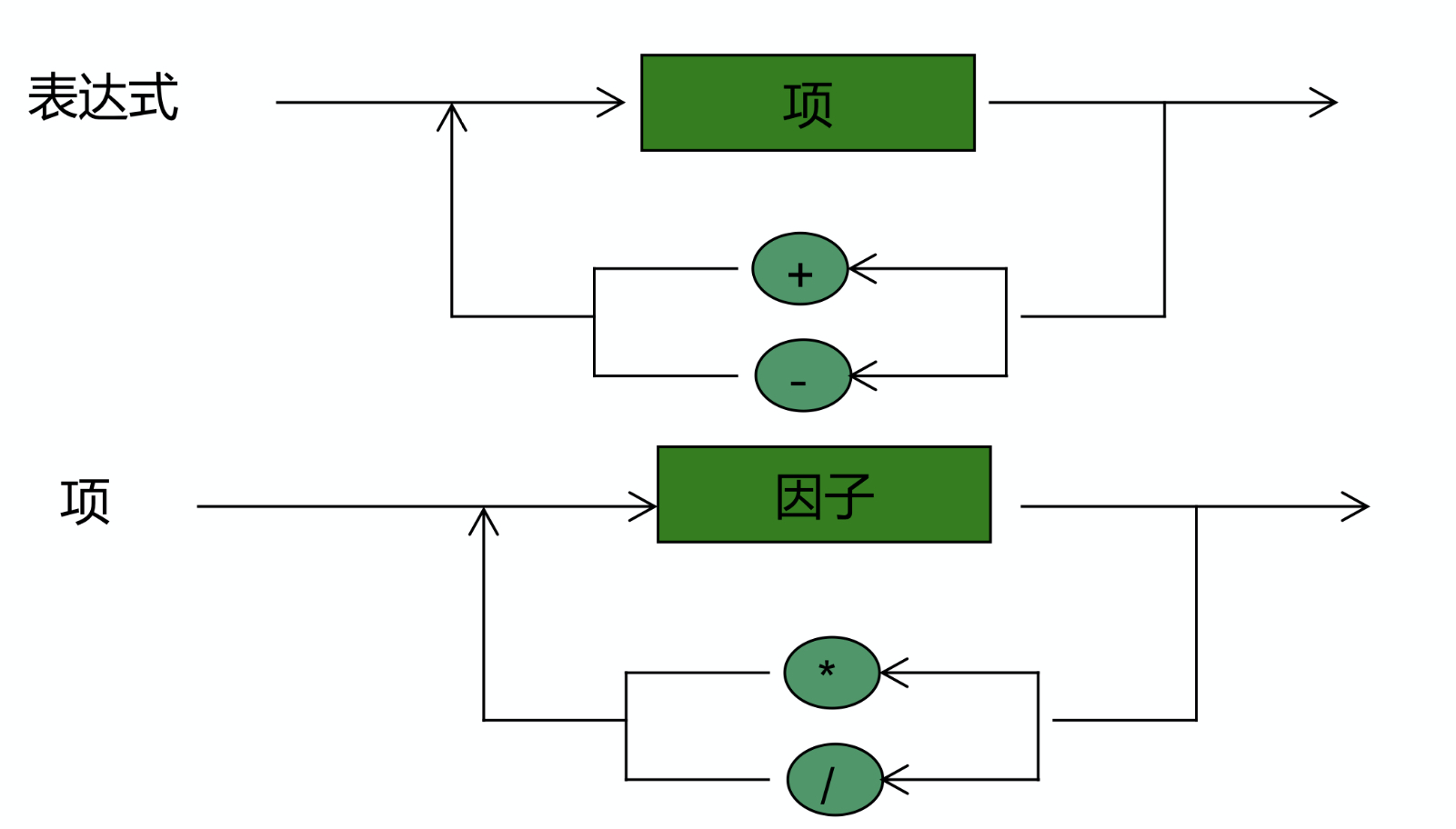
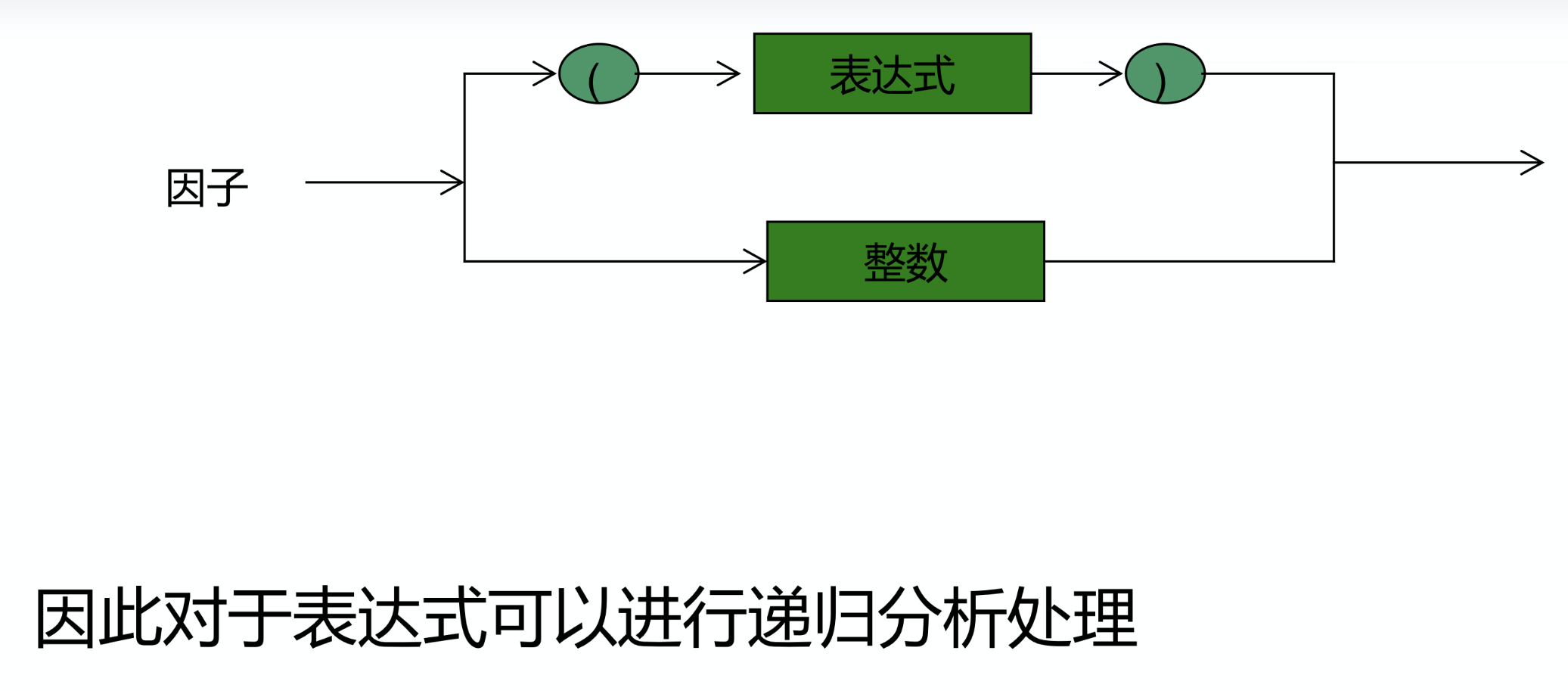
这样的循环定义可以提现运算符的优先性!!终止在一个整数上。
注:
1.isdigit函数:ctype.h 若参数c为阿拉伯数字0~9,则返回非0值,否则返回0。(用来判断char型变量是否为数字好用)
2.cin.peek():其返回值是一个char型的字符,其返回值是指针指向的当前字符,但它只是观测,指针仍停留在当前位置,并不后移。如果要访问的字符是文件结束符,则函数值是EOF(-1)。从输入流中取出字符(仅观测)非常好用
#include<iostream>
#include<cstring>
#include<cstdlib>
using namespace std;
int factor_value();//读入一个因子并返回其值
int term_value();//读入一项并返回其值
int expression_value();//读入一个表达式并返回其值
int main()
{
cout << expression_value()<<endl;
return 0;
}
int expression_value()//求一个表达式的值
{
int result=term_value();//求第一项的值
bool more=true;//看有无新的项
while(more){
char op=cin.peek(); //看一个字符,不取走!
if( op=='+' || op=='-'){
cin.get(); //从输入中取走一个字符
int value= term_value();
if(op=='+') result+=value;
else result -=value;
}
else more =false; //可能是右括号。
}
return result;
}
int term_value(){ //求一个项的值
int result=factor_value(); //求第一个因子的值
while(true) {
char op=cin.peek();
if(op=='*'||op=='/'){
cin.get();
int value =factor_value();
if(op=='*')
result *= value;
else result /= value;
}
else
break;
}
return result;
}
int factor_value(){//求一个因子的值
int result=0;
char c= cin.peek();
if(c=='('){
cin.get();
result=expression_value();
cin.get();
}
else{
while(isdigit(c)){ //读入一个整数,这个方法好用
result = 10*result+c-'0';
cin.get();
c=cin.peek();
}
}
return result;
}
放苹果
题目:把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?5,1,1和1,5,1是同一种分法。
思路:设i个苹果放在k个盘子里放法总数是f(i,k),则
k>i时,f(i,k)=f(i,i)
k<=i时,总方法=有盘子为空的放法+没盘子为空的放法 (强行找出递推关系)
即f(i,k)=f(i,k-1)+f(i-k,k),最后确定边界条件
#include<iostream>
using namespace std;
int f(int m,int n){
if(n>m)
return f(m,m);
if(m==0)
return 1;
if(n<=0)
return 0;
return f(m,n-1)+f(m-n,n);
}
int main(){
int t,m,n;
cin>>t;
while(t--){
cin>>m>>n;
cout<<f(m,n)<<endl;
}
return 0;
}
算24
题目:给出4个小于10的正整数,你可以使用加减乘除4种运算以及括号把这4个数连接起来得到一个表达式。问题是是否存在一种方式使得得到的表达式的结果等于24.(除法定义为实数除法)
思路:n个数算24,必有两个数要先算,这两个数算的结果,和剩余n-2个数,就构成了n-1个数求24的问题,所以先部分枚举先算的两个数,以及这两个数的运算方式。
关键:确定边界条件+浮点数比较是否相等,不能用== !!!
#include<iostream>
#include<cmath>
using namespace std;
double a[5];
#define EPS 1e-6;
bool isZero(double x){
return fabs(x) <=EPS;
}
bool count24(double a[],int n)
{//用数组a里的n个数,计算24
if(n==1){
if(isZero(a[0]-24))
return true;
else
return false;
}
double b[5];
for(int i=0;i<n-1;++i)
for(int j=i+1;j<n;j++){//枚举两个数的组合
int m=0;//还剩下m=n-2个数
for(int k=0;k<n;++k)
if(k!=i&&k!=j)
b[m++]=a[k];//把其余数放入b
b[m]=a[i]+a[j];
if(count24(b,m+1))
return true;
b[m]=a[i]-a[j];
if(count24(b,m+1))
return true;
b[m]=a[j]-a[i];
if(count24(b,m+1))
return true;
b[m]=a[j]*a[i];
if(count24(b,m+1))
return true;
if(!isZero(a[j])){
b[m]=a[i]/a[j];
if(count24(b,m+1))
return true;
}
if(!isZero(a[i])){
b[m]=a[j]/a[i];
if(count24(b,m+1))
return true;
}
}
return false;
}
int main()
{
while(true){
for(int i=0;i<4;++i)
cin>>a[i];
if(isZero(a[0]))
break;
if(count24(a,4))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
return 0;
}
习题解答
作业链接:http://cxsjsx.openjudge.cn/hw202013/
A:Boolean Expressions
#include<iostream>
#include<stack>
using namespace std;
char line[200];char aline[200];
int casenum=0;
void both(stack<int>&a,stack<char>&b){
int m=a.top();a.pop();
int n=a.top();a.pop();
b.pop();a.push(m&n);
}
void res(stack<int>&a,stack<char>&b){
int tmp=a.top();
a.pop();
a.push(!tmp);
b.pop();
}
int solve(int s,int e){
stack<int> a;stack<char> b;
for(int i=s;i<=e;i++){
if (aline[i]=='('){
int count=1;int end;
for(int j=i+1;j<=e;j++){
if(aline[j]=='(') count++;
else if(aline[j]==')') count--;
if(count==0){
end=j;break;
}
}
a.push(solve(i+1,end-1));
i=end;
}
else if(aline[i]=='!') b.push(aline[i]);
else if(aline[i]=='|'){
while(!b.empty()&&b.top()=='!')
res(a,b);
while(!b.empty()&&b.top()=='&')
both(a,b);
b.push('|');
}
else if(aline[i]=='&'){
while(!b.empty()&&b.top()=='!')
res(a,b);
b.push('&');
}
else if(aline[i]=='F') a.push(0);
else if(aline[i]=='V') a.push(1);
}
if(!b.empty()){
while(!b.empty()&&b.top()=='!') res(a,b);
while(!b.empty()&&b.top()=='&') both(a,b);
while(!b.empty()&&b.top()=='|'){
int m=a.top();a.pop();
int n=a.top();a.pop();
a.push(m|n);
b.pop();
}
}
int answer=a.top();
a.pop();
return answer;
}
int main(){
while(cin.getline(line,200)){
casenum++;
int tmp=0;
for(int i=0;line[i]!='\0';i++){
if(line[i]!=' ')
aline[tmp++]=line[i];
}
aline[tmp]='\0';
cout<<"Expression "<<casenum<<": ";
int flag=solve(0,tmp-1);
if(flag) cout<<"V"<<endl;
else cout<<"F"<<endl;
}
return 0;
}
后来借鉴同学的想了一下 有更简洁的思路 一边读入一边处理同时保证bool栈中不超过两个元素
用stringstream对象ss处理也很方便 ss>>c,每次只从流中取出一个字符(sstream自动转换)
#include<iostream>
#include<sstream>
#include<stack>
using namespace std;
stringstream ss;
bool solve(){
stack<bool> b;
stack<char> s;
char c;
bool flag=false;
while(ss>>c,!ss.eof()){
if(c==' ') continue;
if(c==')') return b.top();
if(c=='!') flag ^=1;
if(c=='V') b.push(flag^1),flag=false;
if(c=='F') b.push(flag^0),flag=false;
if(c=='&'||c=='|') s.push(c);
if(c=='(') b.push(flag^solve()),flag=false;
if(b.size()==2){
bool a1=b.top();b.pop();
bool a2=b.top();b.pop();
b.push(s.top()=='&'?a1&&a2:a1||a2);
s.pop();
}
}
return b.top();
}
int main(){
string line;
int num=0;
while(getline(cin,line)){
ss<<line;
cout<<"Expression "<<++num<<": "<<(solve()?'V':'F')<<endl;
ss.clear();
}
return 0;
}
B:文件结构“图”
#include<iostream>
#include<stack>
#include<set>
using namespace std;
string filename[1000];
void solve(int s,int e,int n);
int main(){
string str;
int casenum=1;int filenum=1;
while(getline(cin,str)){
if(str[0]=='*'){
printf("DATA SET %d:\nROOT\n",casenum);
casenum++;
solve(1,filenum-1,0);
getline(cin,str);
if(str[0]=='#') break;
else{
cout<<endl;
filenum=1;
filename[filenum++]=str;
}
}
else filename[filenum++]=str;
}
return 0;
}
void solve(int s,int e,int n){
set<string> a;
for(int i=s;i<=e;i++){
if(filename[i][0]=='f')
a.insert(filename[i]);
else if(filename[i][0]=='d'){
int count=1;
for(int j=0;j<=n;j++)
printf("| ");
printf("%s\n", filename[i].c_str());
for(int j=i+1;j<=e;j++){
if(filename[j][0]=='d') count++;
else if(filename[j][0]==']'){
count--;
if(!count){
if(i!=j-1) solve(i+1,j-1,n+1);
i=j;break;
}
}
}
}
}
while(!a.empty()){
for(int t=0;t<n;t++)
printf("| ");
printf("%s\n", (*(a.begin())).c_str());
a.erase(a.begin());
}
}
C:The Sierpinski Fractal
#include<iostream>
using namespace std;
const int maxn=1025;
char pic[maxn][2*maxn];
void solve(int n,int x,int y){
if(n==1){
pic[x][y]=pic[x+1][y-1]='/';
pic[x][y+1]=pic[x+1][y+2]='\\';
pic[x+1][y]=pic[x+1][y+1]='_';
return;
}
int m= 1<<(n-1);
solve(n-1,x,y);
solve(n-1,x+m,y-m);
solve(n-1,x+m,y+m);
}
int main(){
int n;
while(cin>>n&&n!=0){
int h=(1<<n);
int w=2*h;
for(int i=0;i<=h;i++){
for(int j=0;j<=w;j++)
pic[i][j]=' ';
}
solve(n,1,1<<n);
int k=h+1;
for(int i=1;i<=h;i++){
pic[i][k+i]='\0';
cout<<(pic[i]+1)<<endl;;
}
cout<<endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号