Leetcode - 63. 不同路径 II

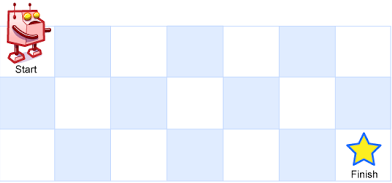
一个机器人位于一个m x n网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用1和0来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-paths-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

（错误）解1 2021/9/9 O(mxn)

def udpate_shang_zuo(dp:list, x:int, y:int, m:int, n:int) -> None:
    # 更新上格
    if x>0 and dp[x-1][y]==0:
        # =0的就别处理了，说明还没准备好
        ### 错误 - 3
        #加了障碍物后，是会存在0的情况，如果这个0的右边和下面都是0，或者都是-1，这种还是需要算的
        #[TODO] 写起来有点繁杂，肯定有更好的解法
        if dp[x][y]==0 or (y<n-1 and dp[x-1][y+1]==0): return
        ### 错误 - 3
        # =-1表示此路不通
        dp[x-1][y]+=dp[x][y] if dp[x][y]!=-1 else 0
        if y<n-1:
            dp[x-1][y]+=dp[x-1][y+1] if dp[x-1][y+1]!=-1 else 0
        udpate_shang_zuo(dp, x - 1, y, m, n)
    # 更新左格
    if y>0 and dp[x][y-1]==0:
        # =0的就别处理了，说明还没准备好
        if dp[x][y]==0 or (x<m-1 and dp[x+1][y-1]==0): return
        dp[x][y-1]+=dp[x][y] if dp[x][y]!=-1 else 0
        if x<m-1:
            dp[x][y-1]+=dp[x+1][y-1] if dp[x+1][y-1]!=-1 else 0
        udpate_shang_zuo(dp, x, y - 1, m, n)
    # 从调试看，=0不处理，最终结果是对的，不会中途停掉，不会漏，暂时没有理解

def uniquePathsWithObstacles(obstacleGrid: list) -> int:
    # 本质上和题62没有区别
    # f(x,y)=f(x,y+1)+f(x+1,y),如果是障碍物就不加
    ### 错误 - 1
    ### 错误 - 2
    #if obstacleGrid[-1][-1]==1: return 0
    if obstacleGrid[-1][-1]==1 or obstacleGrid[0][0]==1: return 0
    ### 错误 - 2
    ### 错误 - 1
    m=obstacleGrid.__len__()
    n=obstacleGrid[0].__len__()
    dp=[[0 for x in range(0,n)] for y in range(0,m)]
    for x in range(0,m):
        for y in range(0,n):
            if obstacleGrid[x][y]==1:
                # 赋个-1表示障碍物
                dp[x][y]=-1
    x=m-1;y=n-1
    dp[x][y]=1
    udpate_shang_zuo(dp,x,y,m,n)
    return dp[0][0]

if __name__ == '__main__':
    '''
    # 2
    obstacleGrid = [[0, 0, 0], [0, 1, 0], [0, 0, 0]]
    print(uniquePathsWithObstacles(obstacleGrid))
    # 1
    obstacleGrid = [[0, 1], [0, 0]]
    print(uniquePathsWithObstacles(obstacleGrid))
    # 0
    obstacleGrid = [[0, 1], [1, 0]]
    print(uniquePathsWithObstacles(obstacleGrid))
    # 0
    obstacleGrid = [[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0]]
    print(uniquePathsWithObstacles(obstacleGrid))
    ### 错误
    # 1, 终点本身是障碍物
    obstacleGrid = [[0, 0], [0, 1]]
    print(uniquePathsWithObstacles(obstacleGrid))
    # 2, 起点本身是障碍物
    obstacleGrid = [[1, 0]]
    print(uniquePathsWithObstacles(obstacleGrid))
    '''
    # 3, 10
    # 如果某个dp的某个位置是0，不一定是没有准备好，也能是这个0的右边和下面是思路，所以它是0
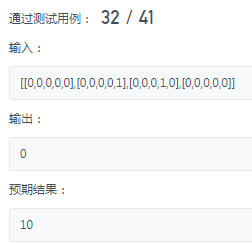
    obstacleGrid=[[0, 0, 0, 0, 0], [0, 0, 0, 0, 1], [0, 0, 0, 1, 0], [0, 0, 0, 0, 0]]
    print(uniquePathsWithObstacles(obstacleGrid))