Leetcode - 39. 组合总和

给定一个无重复元素的正整数数组candidates和一个正整数target，找出candidates中所有可以使数字和为目标数target的唯一组合。
candidates中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。 
对于给定的输入，保证和为target的唯一组合数少于150个。

示例 1：

输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

示例 4：

输入: candidates = [1], target = 1
输出: [[1]]

示例 5：

输入: candidates = [1], target = 2
输出: [[1,1]]

提示：

• 1 <= candidates.length <= 30
• 1 <= candidates[i] <= 200
• candidate 中的每个元素都是独一无二的。
• 1 <= target <= 500

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combination-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

（错误）解1 2021/9/3 O(?)

from collections import defaultdict

def combinationSum(candidates: list, target: int) -> list:
    # 比如[2,3,6,7],7
    # 取2的时候，一定是取2和比自己小的
    # 222,1 ×
    # 取3的时候，一定只能取3和比自己小的
    # 33,1 ×
    # 3,22
    # 发现有重复计算
    # target的范围是[1,500]，不妨从1开始，到target，中间的所有情况都算出来
    # 就像斐波那契数列一样，算出来并保存下来，只不过这里需要全部保存，不能像斐波那契那样只保存2个
    '''
    比如7，
    1,          不存在
    2,
        1+1,    不存在
        2,      [2]
    3,
        1*3,    不存在
        1+2,    不存在
        3,      [3]
    4,
        1*4,    不存在
        1+1+2,  不存在
        1+3,    不存在
        2+2,    [2]+[2]=[2,2]
        3+1,    不存在
        4,      不存在
    '''
    # 这么遍历也比较麻烦，
    # 把每个数，<target的情况都列出来
    # 2, 6:[2,2,2],4:[2,2],2:[2]
    # 3, 6:[3,3],3:[3]
    # 6, 6:[6]
    # 7, 7:[7]
    # 整合一下，
    # 2,[[2]]
    # 3,[[3]]
    # 4,[[2,2]]
    # 6,[[2,2,2],[3,3],[6]]
    # 7,[[7]]
    # 可以放dict，遍历这个dict，查找target-x，是否就是答案？测它

    # 这里不能用集合，res.add(list)不允许，list是unhashable的
    #res=set()
    res=[]
    d=defaultdict(list)
    for x in candidates:
        n=target//x
        while n:
            d[x*n].append([x]*n)
            n-=1
    print(d)
    for x in d.keys():
        v=target-x
        if v==0:
            ### 错误 - 1
            #res.append(d[x][0])
            if x in candidates:
                res.append([x])
            ### 错误 - 1
        if d.get(v):
            for a in d[x]:
                for b in d[v]:
                    # 去重
                    # 1. 用not in的方式
                    ans=sorted(a+b)
                    if ans not in res:
                        res.append(ans)
                    # 2. 也可以用itertools.groupby
    return res

if __name__ == '__main__':
    '''
    print(combinationSum([2,3,6,7],7))
    print(combinationSum([2,3,5],8))
    print(combinationSum([2],1))
    print(combinationSum([1],1))
    print(combinationSum([1],2))
    ### 错误 - 1
    # 1
    print(combinationSum([1,2],2))
    '''
    # 2, [[1,1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,2],[1,1,1,1,1,1,3],[1,1,1,1,1,2,2],[1,1,1,1,2,3],[1,1,1,1,5],[1,1,1,2,2,2],[1,1,1,3,3],[1,1,1,6],[1,1,2,2,3],[1,1,2,5],[1,1,7],[1,2,2,2,2],[1,2,3,3],[1,2,6],[1,3,5],[2,2,2,3],[2,2,5],[2,7],[3,3,3],[3,6]]
    print(combinationSum([2, 7, 6, 3, 5, 1],9))

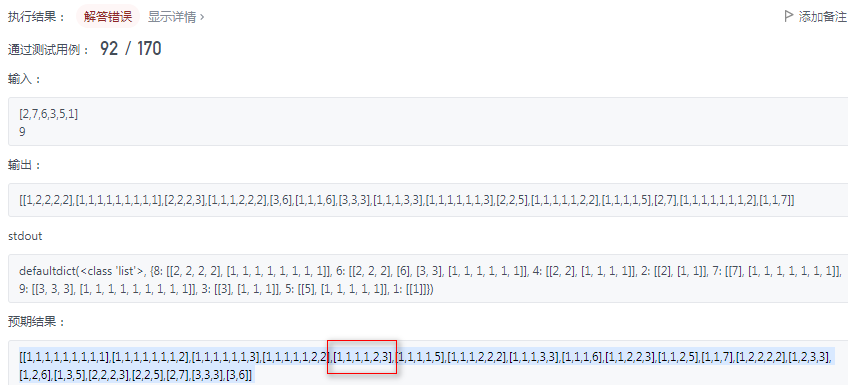
这种解法，没考虑多个数的情况

解1 2021/9/3 O(?)

from collections import defaultdict

def combinationSum(candidates: list, target: int) -> list:
    # 还是得把1到target的全存下来
    # 对于某个数字n来说， 可以是n, 1+(n-1), 2+(n-2), .... n//2+(n-n//2)的组合, 在后面就重复了
    d=defaultdict(list)
    # 把n本身先存起来（也就是candidates数列），这样就是计算1+(n-1),2+(n-2).....
    for x in candidates:
        d[x].append([x])
    i=1
    while i<=target:
        half=i//2
        x=1
        while x<=half:
            if d.get(x) and d.get(i-x):
                for a in d[x]:
                    for b in d[i-x]:
                        ans=sorted(a+b)
                        if ans not in d[i]:
                            d[i].append(ans)
            x+=1
        i+=1
    # print(d)
    return d[target]

if __name__ == '__main__':
    print(combinationSum([2,3,6,7],7))
    print(combinationSum([2,3,5],8))
    print(combinationSum([2],1))
    print(combinationSum([1],1))
    print(combinationSum([1],2))
    ### 错误 - 1
    # 1
    print(combinationSum([1,2],2))
    # 2, [[1,1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,2],[1,1,1,1,1,1,3],[1,1,1,1,1,2,2],[1,1,1,1,2,3],[1,1,1,1,5],[1,1,1,2,2,2],[1,1,1,3,3],[1,1,1,6],[1,1,2,2,3],[1,1,2,5],[1,1,7],[1,2,2,2,2],[1,2,3,3],[1,2,6],[1,3,5],[2,2,2,3],[2,2,5],[2,7],[3,3,3],[3,6]]
    print(combinationSum([2, 7, 6, 3, 5, 1],9))