《Python Cookbook v3.0.0》Chapter3 数字、日期、时间
感谢:
https://github.com/yidao620c/python3-cookbook
如有侵权,请联系我整改。
本文章节会严格按照原书(以便和原书对照,章节标题可能会略有修改),内容会有增删。
3.1 四舍五入(伪)
示例,
>>> round(3.321819,-2)
0.0
>>> round(353.321819,-2)
400.0
>>> round(353.321819,2)
353.32
>>> round(2.5) //attention
2
>>> round(1.5)
2
>>> round(353.321819,-1)
350.0
>>> round(353.321819,4)
353.3218
>>> round(353.321819,3)
353.322
上面有一点(
attention位置)需要注意,2.5并没有四舍五入成3,而是2,
原因是,5这种情况,位于中间位置,round返回离它最近的偶数
对于浮点的精度,大家都知道,cpu的浮点运算只是近似,比如,
>>> a=1.1
>>> b=1.1
>>> a+b
2.2
>>> a=1.3
>>> a+b
2.4000000000000004
这时候,用
round是可以去掉后面的误差,但是没有必要,
日常的运算(非金融领域),这点误差不会有影响。
3.2 精确的浮点运算
from decimal import Decimal
直接看示例,
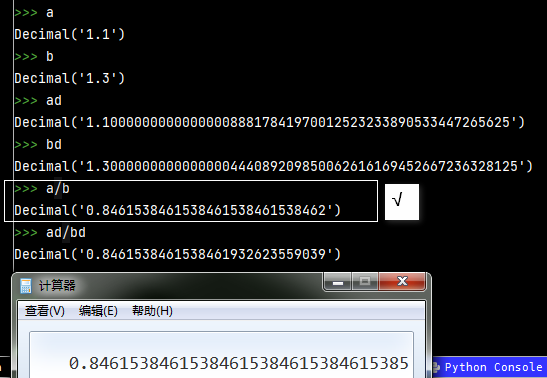
>>> a=Decimal('1.1')
>>> b=Decimal('1.3')
>>> a+b
Decimal('2.4')
>>> a+b==Decimal('2.4')
True
>>> ad=Decimal(1.1)
>>> bd=Decimal(1.3)
>>> ad+bd
Decimal('2.400000000000000133226762955')
>>> bd+ad==Decimal(2.4)
False
>>> Decimal(2.4)
Decimal('2.399999999999999911182158029987476766109466552734375')
所以,从例子也能看出,对于现代计算机,做不到真正的浮点,
Decimal处理的其实是字符串,所以它的效率,比float运算低,
对于非金融领域的,没有必要用Decimal
对于精度,
Decimal精度是准确的,
如果需要控制小数点后几位,可以使用Decimal的
本地上下文 localcontext,
from decimal import localcontext
>>> localcontext()
<decimal.ContextManager object at 0x0000000003A60170>
>>> with localcontext() as ctx:
... ctx.prec = 3
... print(a/b)
0.846
>>> with localcontext() as ctx:
... ctx.prec = 10
... print(a/b)
0.8461538462
3.3 数字的格式化输出
用format,前文已有叙述,这里补充几个,
>>> format(x, '0,.1f') //','是千位分隔符
'1,234.6'
>>> format(x, 'e') //'e'是指数
'1.234568e+03'
>>> format(x, '0.2E')
'1.23E+03'
3.4 进制转换
10 转 其他进制,有bin、oct、hex、format,
其他进制 转 10,有int,
示例,
>>> x = 1234
>>> bin(x)
'0b10011010010'
>>> oct(x)
'0o2322'
>>> hex(x)
'0x4d2'
>>> format(x, 'b')
'10011010010'
>>> format(x, 'o')
'2322'
>>> format(x, 'x') //注意,format,16进制是‘x’,不是‘h’
'4d2'
>>> x = -1234
>>> format(x, 'b')
'-10011010010'
>>> format(2**32 + x, 'b')
'11111111111111111111101100101110'
>>> format((2<<32) + x, 'x')
'fffffb2e'
>>> int('4d2', 16)
1234
>>> int('10011010010', 2)
1234
3.5 字节到大整数的打包与解包
[TODO]
3.6 复数的数学运算
[TODO]
3.7 无穷和NaN
NaN指not a number,
>>> a=float('inf')
>>> b=float('-inf')
>>> -a==b
True
>>> import math
>>> math.isinf(a)
True
>>> math.isinf(b)
True
>>> c = float('nan')
>>> math.isnan(c)
True
3.8 分数运算
from fractions import Fraction
示例,
>>> a = Fraction(5, 4)
>>> b = Fraction(7, 16)
>>> a*b
Fraction(35, 64)
>>> c = a * b
>>> c.numerator
35
>>> c.denominator
64
>>> float(c)
0.546875
>>> c.limit_denominator(8) //限制分母的最大值,不要怀疑,它返回的结果是最接近原值的
Fraction(4, 7)
>>> c.limit_denominator(32)
Fraction(6, 11)
>>> x = 3.75
>>> Fraction(*x.as_integer_ratio()) //同Fraction(x)
Fraction(15, 4)
3.9 数组运算
import numpy as np
两个数组的运算是没法用数组推导的。
>>> ax=np.array([1,23])
>>> ay=np.array([14.12,77])
>>> ax+ay
array([ 15.12, 100. ])
>>> ax*ay
array([ 14.12, 1771. ])
>>> ax+3
array([ 4, 26])
>>> def f(x):
... return x**3+3*x**2-7*x+15
>>> f(ax)
array([ 12, 13608])
>>> f(ay)
array([ 3329.449728, 473796. ])
>>> np.min(ax)
1
>>> np.sqrt(ax)
array([1. , 4.79583152])
>>> np.cos(ax)
array([ 0.54030231, -0.53283302])
numpy几乎所有的数学运算都支持,用numpy比遍历数组并使用math效率高,
数组运算,允许使用numpy的情况下,就使用numpy
numpy可以处理的数组非常大,比list大得多,但太大了(上百G)也不行
>>> grid=np.zeros(shape=(1920,1080),dtype=float)
>>> grid
array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]])
>>> grid += 10
>>> grid
array([[10., 10., 10., ..., 10., 10., 10.],
[10., 10., 10., ..., 10., 10., 10.],
[10., 10., 10., ..., 10., 10., 10.],
...,
[10., 10., 10., ..., 10., 10., 10.],
[10., 10., 10., ..., 10., 10., 10.],
[10., 10., 10., ..., 10., 10., 10.]])
>>> np.sin(grid)
array([[-0.54402111, -0.54402111, -0.54402111, ..., -0.54402111,
-0.54402111, -0.54402111],
[-0.54402111, -0.54402111, -0.54402111, ..., -0.54402111,
-0.54402111, -0.54402111],
[-0.54402111, -0.54402111, -0.54402111, ..., -0.54402111,
-0.54402111, -0.54402111],
...,
[-0.54402111, -0.54402111, -0.54402111, ..., -0.54402111,
-0.54402111, -0.54402111],
[-0.54402111, -0.54402111, -0.54402111, ..., -0.54402111,
-0.54402111, -0.54402111],
[-0.54402111, -0.54402111, -0.54402111, ..., -0.54402111,
-0.54402111, -0.54402111]])
>>> grid=np.zeros(shape=(192000,108000),dtype=float)
Traceback (most recent call last):
File "<input>", line 1, in <module>
numpy.core._exceptions._ArrayMemoryError: Unable to allocate 154. GiB for an array with shape (192000, 108000) and data type float64
>>> grid=np.zeros(shape=(19200,10800),dtype=float)
numpy可以很方便的处理多维数组,不知是否能在量子力学上有所施展
示例,
>>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
>>> a
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>> a[0] //元素0,这里是行0
array([1, 2, 3, 4])
>>> a[:] //所有
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>> a[:,0] //列0,以行的形式表示
array([1, 5, 9])
>>> a[:,0:1] //列0,以列的形式表示
array([[1],
[5],
[9]])
>>> a[1:3] //行1,行2
array([[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>> a[1:] //行1到结束
array([[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>> a[:,1:3] //列1,列2
array([[ 2, 3],
[ 6, 7],
[10, 11]])
>>> a[:,1:] //列1到结束
array([[ 2, 3, 4],
[ 6, 7, 8],
[10, 11, 12]])
>>> a[1:3,1:3] //行1、行2,列1、列2,取交集
array([[ 6, 7],
[10, 11]])
同样的,上述返回,都支持数学运算,还支持下面的条件赋值
>>> a
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>> np.where(a<10,a,-1)
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, -1, -1, -1]])
3.10 矩阵、线性代数
这正是我需要的,多么美妙!
示例,
>>> a=np.array([[1,2],[4,6]])
>>> b=np.array([[3,2],[1,7]])
>>> a
array([[1, 2],
[4, 6]])
>>> b
array([[3, 2],
[1, 7]])
>>> a*b
array([[ 3, 4],
[ 4, 42]])
>>> ma=np.matrix([[1,2],[4,6]])
>>> mb=np.matrix([[3,2],[1,7]])
>>> ma
matrix([[1, 2],
[4, 6]])
>>> mb
matrix([[3, 2],
[1, 7]])
>>> ma*mb
matrix([[ 5, 16],
[18, 50]])
矩阵的
翻转和逆矩阵
>>> ma.T
matrix([[1, 4],
[2, 6]])
>>> ma.I
matrix([[-3. , 1. ],
[ 2. , -0.5]])
>>> ma * ma.I
matrix([[1., 0.],
[0., 1.]])
import numpy.linalg中包含了更多有用的函数,
参考numpy官网:http://www.numpy.org
3.11 随机选择
import random
注意,random是伪随机,是确定性算法,也是通过seed来实现的,
random.seed() # Seed based on system time or os.urandom()
random.seed(12345) # Seed based on integer given
random.seed(b'bytedata') # Seed based on byte data
示例,
>>> import random
>>> values = [1, 2, 3, 4, 5, 6]
>>> random.choice(values) //从中随机选择1个
2
>>> random.sample(values, 2) //随机采样,本例采2个
[6, 2]
>>> random.shuffle(values) //随机打乱
>>> values
[2, 4, 6, 5, 3, 1]
>>> random.randint(0,10) //[0-10]范围随机生成1个int,没有.randfloat
2
>>> random.random() //随机产生一个[0-1]的浮点,没有random(0,10)
0.9406677561675867
>>> random.getrandbits(200) //随机产生N位二进制数
335837000776573622800628485064121869519521710558559406913275
3.12 日期
from datetime import timedelta
from datetime import datetime
示例,
>>> a = timedelta(days=2, hours=6)
>>> b = timedelta(hours=4.5)
>>> c = a + b
>>> c.days
2
>>> c.seconds
37800
>>> a = datetime(2012, 9, 23)
>>> print(a + timedelta(days=10))
2012-10-03 00:00:00
>>> now = datetime.today()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号