第二次大作业
前言
时间过的很快啊,总于不用再跟这些多边形打交道了 多边形这坎总算跨完了。题量虽然不多,知识点多且复杂,真的很难,但也真的有学到很多知识。在期中考试中,考察了继承与多态的运用还有泛型容器。这次的四边形与五边形进一步考察了正则表达式的使用,还有关于点在多边形内的情况与计算,相关多边形一些属性的判断计算。当涉及这些复杂多边形时,就体会到之前点线三角形的相关计算简单很多了。
接下来是详细分析...我把代码折叠了,这样更简洁,点+号就可以看啦。
PTA第四次大作业
7-1 sdut-String-2 识蛟龙号载人深潜,立科技报国志(II)(正则表达式)
这道题还是比较简单的,主要是考察了正则表达式的运用。我记录数字运用了容器,感觉很好用,不用考虑数组越界问题。

1 import java.util.ArrayList; 2 import java.util.Scanner; 3 import java.util.regex.Matcher; 4 import java.util.regex.Pattern; 5 public class Main { 6 7 public static void main(String[] args) { 8 9 Scanner in = new Scanner(System.in); 10 ArrayList <Integer> num =new ArrayList <Integer> (); 11 String s = in.nextLine(); 12 for(int i=0;!s.equals("end");i++) { 13 String regex ="[0-9]+"; 14 Pattern p=Pattern.compile(regex); 15 Matcher m=p.matcher(s); 16 num.add(count(m)); 17 s = in.nextLine(); 18 } 19 show(num); 20 } 21 22 public static int count(Matcher m) { 23 int mum =0; 24 int mm=0; 25 while(m.find()) { 26 mum+=Integer.parseInt(m.group()); 27 } 28 return mum; 29 } 30 31 public static void show(ArrayList<Integer> sum) { 32 for(Integer s:sum) { 33 System.out.println(s); 34 } 35 } 36 }
7-2 点线形系列4-凸四边形的计算

import java.util.Scanner; import java.text.DecimalFormat; public class Main { public static class Point { double x; double y; } public static void main(String[] args) { Scanner in = new Scanner(System.in); String s=new String(); s=in.nextLine(); String s1=s.substring(0, 2); String regex1 = "[1-5]+:"; boolean flag = s1.matches(regex1);//判断功能 if(!flag) { System.out.print("Wrong Format"); System.exit(0); } s=s.substring(2); int num = Integer.parseInt(s1.substring(0,1)); check(s,num); } /* * 输入:两个点 * 处理:判定两点是否重合 * 输出:points coincide * */ public static void prime(Point a,Point b) { if(Math.abs(a.x-b.x)<0.001&&Math.abs(a.y-b.y)<0.001) { System.out.print("points coincide"); System.exit(0); } } /* * 输入:字符串和数字 * 处理:检查输入格式是否正确并且得到点坐标,并进入相应的选项计算 * 输出: * */ public static void check(String s,int n){ Quadrangle n1=new Quadrangle(); int end=0; int begin=0; String s2=new String(); int i=0; int m=0; int j=0; String s3=new String(); String s4=new String(); if(n==1||n==2||n==3) { j=8; } else if(n==4) { j=12; } else { j=10; } double[] array =new double[j]; while(s.length()>0) { if(i==j) { System.out.print("wrong number of points"); System.exit(0); } end=s.indexOf(' '); if(end==-1) { s2=s.substring(begin); } else { s2=s.substring(begin, end); } String regex = "[+-]?([0-9]+[.])?[0-9]+,[+-]?([0-9]+[.])?[0-9]+"; boolean flag = s2.matches(regex);//判断功能 if(!flag) { System.out.print("Wrong Format"); System.exit(0); } m=s2.indexOf(','); s3=s2.substring(begin, m); s4=s2.substring(m+1); array[i]=Double.parseDouble(s3); array[i+1]=Double.parseDouble(s4); i=i+2; if(end!=-1) { s=s.substring(end+1); } else { s=s.substring(s.length()); } } if(i<j-1) { System.out.print("wrong number of points"); System.exit(0); } Point m1=new Point(); Point m2=new Point(); Point w1=new Point(); if(j==8) { n1.a.x=array[0]; n1.a.y=array[1]; n1.b.x=array[2]; n1.b.y=array[3]; n1.c.x=array[4]; n1.c.y=array[5]; n1.d.x=array[6]; n1.d.y=array[7]; prime(n1.a,n1.b);prime(n1.a,n1.c);prime(n1.a,n1.d);prime(n1.c,n1.b); prime(n1.d,n1.b);prime(n1.c,n1.d); } else if(j==12) { m1.x=array[0]; m1.y=array[1]; m2.x=array[2]; m2.y=array[3]; n1.a.x=array[4]; n1.a.y=array[5]; n1.b.x=array[6]; n1.b.y=array[7]; n1.c.x=array[8]; n1.c.y=array[9]; n1.d.x=array[10]; n1.d.y=array[11]; prime(m1,m2); } else { w1.x=array[0]; w1.y=array[1]; n1.a.x=array[2]; n1.a.y=array[3]; n1.b.x=array[4]; n1.b.y=array[5]; n1.c.x=array[6]; n1.c.y=array[7]; n1.d.x=array[8]; n1.d.y=array[9]; } switch(n) { case 1:Quadrangle.prime_sbx(n1);break; case 2:Quadrangle.prime_xz(n1);break; case 3:Quadrangle.prime_ta(n1);break; case 4:Quadrangle.prime_jd(m1, m2, n1);break; case 5:Quadrangle.prime_in(w1, n1);break; } } public static class Quadrangle { Point a=new Point(); Point b=new Point(); Point c=new Point(); Point d=new Point(); /* * 输入:四个点坐标 * 处理:判断是否是四边形、平行四边形 * 输出:true/false, * */ public static void prime_sbx(Quadrangle n1) { if (prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) { System.out.print("true "); } else { System.out.print("false "); } if(Math.abs((n1.a.x+n1.c.x)-(n1.b.x+n1.d.x))<0.0001&&Math.abs((n1.a.y+n1.c.y)-(n1.b.y+n1.d.y))<0.0001) { System.out.print("true"); } else { System.out.print("false"); } } /* * 输入:三个坐标 * 处理:判断是否成一条直线 * 输出: true false * */ public static boolean prime_zx(Point a,Point b,Point c) { if (prime((c.y - b.y) * (c.x - a.x) ,(c.y - a.y) * (c.x - b.x))) return false; else return true; } /* * 输入:四个点坐标 * 处理:判断是否是菱形、矩形、正方形 * 输出: true false 结果之间以一个英文空格符分隔 * */ public static void prime_xz(Quadrangle n1) { if (!(prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) ){ System.out.print("not a quadrilateral"); System.exit(0); } boolean p=prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d); boolean q=prime(distant(n1.a,n1.b),distant(n1.b,n1.c))&&prime(distant(n1.c,n1.d),distant(n1.b,n1.c))&&prime(distant(n1.c,n1.d),distant(n1.d,n1.a)); boolean v=prime_zj(n1.a,n1.b,n1.d)&&prime_zj(n1.b,n1.a,n1.c)&&prime_zj(n1.c,n1.b,n1.d); if(p&&q) { System.out.print("true "); } else { System.out.print("false "); } if(p&&v) { System.out.print("true "); } else { System.out.print("false "); } if(p&&q&&v){ System.out.print("true"); } else { System.out.print("false"); } } /* * 输入:两个浮点数 * 处理:判断是否相等 * 输出: true false * */ public static boolean prime(double a,double b) { if(Math.abs(a-b)<0.000001) //相等 return true; else return false; } /* * 输入:三个点,a,b,c * 处理:判断构成的角A是否为直角 * 输出: true false * */ public static boolean prime_zj(Point a,Point b,Point c) { double x1=b.x-a.x; double y1=b.y-a.y; double x2=c.x-a.x; double y2=c.y-a.y; if(prime(x1*x2,(-1)*y2*y1)) { return true; } else return false; } /* * 输入:两个点坐标 * 处理:计算距离 * 输出: * */ public static double distant(Point a,Point b) { double dis=0; double m; m=Math.pow(a.x-b.x,2.0)+Math.pow(a.y-b.y,2.0); dis=Math.pow(m, 0.5); return dis; } /* * 输入:四个点坐标 * 处理:判断是凹四边形(false)还是凸四边形(true) * 输出:输出四边形周长、 面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral" * */ public static void prime_ta(Quadrangle n1) { if (!(prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) ){ System.out.print("not a quadrilateral"); System.exit(0); } double t1 = (n1.d.x-n1.a.x)*(n1.b.y-n1.a.y)-(n1.d.y-n1.a.y)*(n1.b.x-n1.a .x); double t2=(n1.a.x-n1.b.x)*(n1.c.y-n1.b.y)-(n1.a.y-n1.b.y)*(n1.c.x-n1.b.x); double t3= (n1.b.x-n1.c.x)*(n1.d.y-n1.c.y)-(n1.b.y-n1.c.y)*(n1.d.x-n1.c.x); double t4= (n1.c.x-n1.d.x)*(n1.a.y-n1.d.y)-(n1.c.y-n1.d.y)*(n1.a.x-n1.d.x); if(t1*t2*t3*t4 >0) { System.out.print("true "); } else { System.out.print("false "); } double zc=0; double mj=0; DecimalFormat df =new DecimalFormat("0.0##"); zc=distant(n1.a,n1.b)+distant(n1.b,n1.c)+distant(n1.c,n1.d)+distant(n1.d,n1.a); mj= Math.abs(n1.a.x * n1.b.y + n1.b.x * n1.c.y + n1.c.x * n1.a.y - n1.a.y * n1.b.x - n1.b.y * n1.c.x - n1.c.y * n1.a.x) / 2.0+ Math.abs(n1.a.x * n1.d.y + n1.d.x * n1.c.y + n1.c.x * n1.a.y - n1.a.y * n1.d.x - n1.d.y * n1.c.x - n1.c.y * n1.a.x) / 2.0; System.out.print(df.format(zc)+" "+df.format(mj)); } /* * 输入:六个点坐标 * 处理:前两个点构成一条直线,后四个点构成一个四边形或三角形,输 出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大 输出四边形(或三角形)被直线分割成两部分的面积(不换行) * 输出:若直线与四边形或三角形的 一条边线重合,输出"The line is coincide with one of the lines"。 若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。 * */ public static int ControlFloat(double x)//精度控制 { if(Math.abs(x)<1e-11) return 0; return (x>0)?1:-1; } public static double ChaJi(Point p0,Point p1,Point p2)//叉积 { return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); } public static int intersect(Point a,Point b,Point c,Point d,Point j)//判断直线ab与线段cd是否有交点,有则输出x坐标 { double s1=ChaJi(a,b,c); double s2=ChaJi(a,b,d); int d1=ControlFloat(s1); int d2=ControlFloat(s2); if(d1*d2>0) { return 3; } else if(d1==0&&d2==0) { return 2; } else { if(prime(b.x,a.x)){ double k1=(d.y-c.y)/(d.x-c.x); j.y=a.y; j.x=(d.y-c.y)/k1 +c.x; } else { double k1=(d.y-c.y)/(d.x-c.x); double k=(b.y-a.y)/(b.x-a.x); j.x=(k*a.x-k1*c.x+c.y-a.y)/(k-k1); j.y=k*j.x-k*a.x+a.y; } return 1; } } public static Point re_point1(Point a,Point b,Point c) { Point t=new Point(); t=a; if(a.x>b.x) { t=b; if(b.x>c.x) t=c; } else { if(a.x>c.x) t=c; } return t; //最左侧点 } public static Point re_point2(Point a,Point b,Point c) { Point t=new Point(); t=a; if(a.x<b.x) { t=b; if(b.x<c.x) t=c; } else { if(a.x<c.x) t=c; } return t; //最右侧点 } public static void output_jd(Point a1,Point b1,Point c1,Point j1,Point j2) {//输出面积 三角形 double a=distant(j1,a1); double b=distant(j2,a1); double c=distant(j1,j2); double p = (a + b + c) / 2; double d=distant(a1,b1); double e=distant(b1,c1); double f=distant(c1,a1); double p1=(d+e+f)/2; double s1=Math.sqrt(p * (p - a) * (p - b) * (p - c)); double s2=Math.sqrt(p1 *(p1-d)*(p1-e)*(p1-f))-s1; double zj=0; if(s1>s2) { zj=s1;s1=s2;s2=zj; } DecimalFormat df =new DecimalFormat("0.0##"); System.out.print("2 "+df.format(s1)+" "+df.format(s2)); } public static void output_jd1(Point a1,Point b1,Point c1,Point d1,Point j1,Point j2) {//输出面积 四边形不对边 double a=distant(j1,b1); double b=distant(j2,b1); double c=distant(j1,j2); double p = (a + b + c) / 2; double s1=Math.sqrt(p * (p - a) * (p - b) * (p - c))*2; double s2=( Math.abs(a1.x * b1.y + b1.x * c1.y + c1.x * a1.y - a1.y * b1.x - b1.y * c1.x - c1.y * a1.x) / 2.0+ Math.abs(a1.x * d1.y + d1.x * c1.y + c1.x * a1.y - a1.y * d1.x - d1.y * c1.x - c1.y * a1.x) / 2.0)-s1; double zj=0; if(s1>s2) { zj=s1;s1=s2;s2=zj; } DecimalFormat df =new DecimalFormat("0.0##"); System.out.print("2 "+df.format(s1)+" "+df.format(s2)); } public static void output_jd2(Point a1,Point b1,Point c1,Point d1,Point j1,Point j2) {//输出面积 四边形对边特殊版 double s1=Math.abs(a1.x * b1.y + b1.x * j1.y + j1.x * a1.y - a1.y * b1.x - b1.y * j1.x - j1.y * a1.x)/2.0 + Math.abs(a1.x * j2.y + j2.x * j1.y + j1.x * a1.y - a1.y * j2.x - j2.y * j1.x - j1.y * a1.x) /2.0; double s2=( Math.abs(a1.x * b1.y + b1.x * c1.y + c1.x * a1.y - a1.y * b1.x - b1.y * c1.x - c1.y * a1.x) / 2.0+ Math.abs(a1.x * d1.y + d1.x * c1.y + c1.x * a1.y - a1.y * d1.x - d1.y * c1.x - c1.y * a1.x) / 2.0)-s1; double zj=0; if(s1>s2) { zj=s1;s1=s2;s2=zj; } DecimalFormat df =new DecimalFormat("0.0##"); System.out.print("2 "+df.format(s1)+" "+df.format(s2)); } public static boolean prime_gdian(Point a,Point b) { if(prime(a.x,b.x)&&prime(a.y,b.y)) { return true; } return false; } public static boolean judge(Point a,Point b,Point c,Point d) { //快速排斥实验 if ((a.x > b.x ? a.x : b.x) < (c.x < d.x ? c.x : d.x) || (a.y > b.y ? a.y : b.y) < (c.y < d.y ? c.y : d.y) || (c.x > d.x ? c.x : d.x) < (a.x < b.x ? a.x : b.x) || (c.y > d.y ? c.y : d.y) < (a.y < b.y ? a.y : b.y)) { return false; } //跨立实验 if ((((a.x - c.x)*(d.y - c.y) - (a.y - c.y)*(d.x - c.x))* ((b.x - c.x)*(d.y - c.y) - (b.y - c.y)*(d.x - c.x))) > 0 || (((c.x - a.x)*(b.y - a.y) - (c.y - a.y)*(b.x - a.x))* ((d.x - a.x)*(b.y - a.y) - (d.y - a.y)*(b.x - a.x))) > 0) { return false; } return true; } public static void prime_jd(Point m1,Point m2,Quadrangle n1) { Point[] w=new Point[4]; Point[] t= new Point[3]; for(int i=0;i<3;i++) { t[i]=new Point(); } for(int i=0;i<4;i++) { w[i]=new Point(); } int[] index=new int[4]; int jd=0; if(intersect(m1,m2,n1.a,n1.b,t[0])==2||intersect(m1,m2,n1.b,n1.c,t[0])==2||intersect(m1,m2,n1.c,n1.d,t[0])==2||intersect(m1,m2,n1.d,n1.a,t[0])==2) { System.out.print("The line is coincide with one of the lines"); System.exit(0); } if (!(prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) ){ if(judge(n1.a,n1.b,n1.c,n1.d)||judge(n1.b,n1.c,n1.d,n1.a)) { System.out.print("not a quadrilateral or triangle"); System.exit(0); } if(!(prime_zx(n1.a,n1.b,n1.c))&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d) ) { // a,c d n1.a=re_point1(n1.a,n1.b,n1.c); n1.c=re_point2(n1.a,n1.b,n1.c); if(intersect(m1,m2,n1.a,n1.c,t[0])==1) { index[jd]=0;jd++; } if(intersect(m1,m2,n1.c,n1.d,t[1])==1) { index[jd]=1; jd++; } if(intersect(m1,m2,n1.d,n1.a,t[2])==1) { index[jd]=2;jd++; } if(jd==1) { System.out.print(jd); } if(jd==2) { for(int i=0;i<2;i++) { for(int j=i+1;j<2;j++) { if(prime_gdian(t[i],t[j])) { jd--; } } } if(jd==1) { System.out.print(jd); System.exit(0); } if(index[0]==0&&index[1]==1) { output_jd(n1.c,n1.d,n1.a,t[0],t[1]); } if(index[0]==0&&index[1]==2) { output_jd(n1.a,n1.c,n1.d,t[0],t[2]); } if(index[0]==1&&index[1]==2) { output_jd(n1.d,n1.a,n1.c,t[1],t[2]); } } } else if((prime_zx(n1.a,n1.b,n1.c))&&!prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) { //a ,b,d n1.b=re_point1(n1.b,n1.c,n1.d); n1.d=re_point1(n1.b,n1.c,n1.d); if(intersect(m1,m2,n1.a,n1.b,t[0])==1) { index[jd]=0;jd++; } if(intersect(m1,m2,n1.b,n1.d,t[1])==1) { index[jd]=1; jd++; } if(intersect(m1,m2,n1.d,n1.a,t[2])==1) { index[jd]=2;jd++; } if(jd==1) { System.out.print(jd); } if(jd==2) { for(int i=0;i<2;i++) { for(int j=i+1;j<2;j++) { if(prime_gdian(t[i],t[j])) { jd--; } } } if(jd==1) { System.out.print(jd); System.exit(0); } if(index[0]==0&&index[1]==1) { output_jd(n1.b,n1.a,n1.d,t[0],t[1]); } if(index[0]==0&&index[1]==2) { output_jd(n1.a,n1.b,n1.d,t[0],t[2]); } if(index[0]==1&&index[1]==2) { output_jd(n1.d,n1.a,n1.b,t[1],t[2]); } } } else if((prime_zx(n1.a,n1.b,n1.c))&&prime_zx(n1.b,n1.c,n1.d)&&!prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) { //a,,d b n1.a=re_point1(n1.a,n1.c,n1.d); n1.d=re_point1(n1.a,n1.c,n1.d); if(intersect(m1,m2,n1.a,n1.b,t[0])==1) { index[jd]=0;jd++; } if(intersect(m1,m2,n1.b,n1.d,t[1])==1) { index[jd]=1; jd++; } if(intersect(m1,m2,n1.d,n1.a,t[2])==1) { index[jd]=2;jd++; } if(jd==1) { System.out.print(jd); } if(jd==2) { for(int i=0;i<2;i++) { for(int j=i+1;j<2;j++) { if(prime_gdian(t[i],t[j])) { jd--; } } } if(jd==1) { System.out.print(jd); System.exit(0); } if(index[0]==0&&index[1]==1) { output_jd(n1.b,n1.a,n1.d,t[0],t[1]); } if(index[0]==0&&index[1]==2) { output_jd(n1.a,n1.b,n1.d,t[0],t[2]); } if(index[0]==1&&index[1]==2) { output_jd(n1.d,n1.a,n1.b,t[1],t[2]); } } } else if((prime_zx(n1.a,n1.b,n1.c))&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&!prime_zx(n1.a,n1.b,n1.d)) { //a,,d c n1.a=re_point1(n1.a,n1.b,n1.d); n1.d=re_point1(n1.a,n1.b,n1.d); if(intersect(m1,m2,n1.a,n1.c,t[0])==1) { index[jd]=0;jd++; } if(intersect(m1,m2,n1.c,n1.d,t[1])==1) { index[jd]=1; jd++; } if(intersect(m1,m2,n1.d,n1.a,t[2])==1) { index[jd]=2;jd++; } if(jd==1) { System.out.print(jd); } if(jd==2) { for(int i=0;i<2;i++) { for(int j=i+1;j<2;j++) { if(prime_gdian(t[i],t[j])) { jd--; } } } if(jd==1) { System.out.print(jd); System.exit(0); } if(index[0]==0&&index[1]==1) { output_jd(n1.c,n1.a,n1.d,t[0],t[1]); } if(index[0]==0&&index[1]==2) { output_jd(n1.a,n1.c,n1.d,t[0],t[2]); } if(index[0]==1&&index[1]==2) { output_jd(n1.d,n1.a,n1.c,t[1],t[2]); } } } else { System.out.print("not a quadrilateral or triangle"); System.exit(0); } } else if(prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)){ if(intersect(m1,m2,n1.a,n1.b,w[0])==1) { index[jd]=0;jd++; } if(intersect(m1,m2,n1.b,n1.c,w[1])==1) { index[jd]=1; jd++; } if(intersect(m1,m2,n1.c,n1.d,w[2])==1) { index[jd]=2;jd++; } if(intersect(m1,m2,n1.d,n1.a,w[3])==1) { index[jd]=3;jd++; } for(int i=0;i<4;i++) { for(int j=i+1;j<4;j++) { if(prime_gdian(w[i],w[j])) { jd=jd-1; } } } jd--; if(jd!=2) { System.out.print(jd); } if(jd==2) { if(index[0]==0&&index[1]==1) { output_jd1(n1.a,n1.b,n1.c,n1.d,w[0],w[1]); } if(index[0]==0&&index[1]==2) { output_jd2(n1.b,n1.c,n1.a,n1.d,w[0],w[2]); } if(index[0]==0&&index[1]==3) { output_jd1(n1.d,n1.a,n1.b,n1.c,w[0],w[3]); } if(index[0]==1&&index[1]==2) { output_jd1(n1.b,n1.c,n1.d,n1.a,w[1],w[2]); } if(index[0]==1&&index[1]==3) { output_jd2(n1.c,n1.a,n1.b,n1.d,w[1],w[3]); } if(index[0]==2&&index[1]==3) { output_jd1(n1.c,n1.d,n1.a,n1.b,w[2],w[3]); } } } } /* * 输入:五个点坐标 * 处理:输出第一个是否在后四个点所构成的四边形(限定为凸四边形, 不考虑凹四边形)或三角形(判定方法见选项 4)的内部(若是四边形输出 in the quadrilateral/outof the quadrilateral, 若是三角形输出 in the triangle/outof the triangle)。 如果点在多边形的某条边上,输出"on the triangle 或者 on the quadrilateral"。 若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。 * */ public static int intersect1(Point a,Point b,Point c,Point d) { double s1=ChaJi(a,b,c); double s2=ChaJi(a,b,d); int d1=ControlFloat(s1); int d2=ControlFloat(s2); if(d1*d2>0) { return 1; } else if(d1*d2==0){ return 0; } else return -1; } /* 判断点是否在线段上 */ public static boolean prime_inline(Point pt_start, Point pt_end, Point pt_hit, double linesize){ if (((pt_hit.x - pt_start.x) * (pt_hit.x - pt_end.x) + (pt_hit.y - pt_start.y) * (pt_hit.y - pt_end.y)) < 0){//必须是钝角 //计算点到直线的距离 double B = -(pt_end.x - pt_start.x); double A = pt_end.y - pt_start.y; double C = -(A * pt_start.x + B * pt_start.y); double t = A * pt_hit.x + B * pt_hit.y + C; double dd = (t * t) / (A * A + B * B); if (dd <= linesize * linesize){ return true; } } return false; } public static void prime_in(Point p,Quadrangle n1) { if (!(prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) ){ if(judge(n1.a,n1.b,n1.c,n1.d)||judge(n1.b,n1.c,n1.d,n1.a)) { System.out.print("not a quadrilateral or triangle"); System.exit(0); } if(!(prime_zx(n1.a,n1.b,n1.c))&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d) ) { // a,c d n1.a=re_point1(n1.a,n1.b,n1.c); n1.c=re_point2(n1.a,n1.b,n1.c); if(prime_inline(n1.a,n1.c,p,distant(n1.a,n1.c))|| prime_inline(n1.c,n1.d,p,distant(n1.c,n1.d))|| prime_inline(n1.d,n1.a,p,distant(n1.d,n1.a))) { System.out.print("on the triangle"); System.exit(0); } if(intersect1(p,n1.a,p,n1.c)*intersect1(p,n1.c,p,n1.d)>=0) { System.out.print("in the triangle"); } else { System.out.print("outof the triangle"); } } else if((prime_zx(n1.a,n1.b,n1.c))&&!prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) { //a ,b,d n1.b=re_point1(n1.b,n1.c,n1.d); n1.d=re_point1(n1.b,n1.c,n1.d); if(prime_inline(n1.a,n1.b,p,distant(n1.a,n1.b))||prime_inline(n1.b,n1.d,p,distant(n1.b,n1.d))||prime_inline(n1.d,n1.a,p,distant(n1.d,n1.a))) { System.out.print("on the triangle"); System.exit(0); } if(intersect1(p,n1.a,p,n1.b)*intersect1(p,n1.b,p,n1.c)>=0) { System.out.print("in the triangle"); } else { System.out.print("outof the triangle"); } } else if((prime_zx(n1.a,n1.b,n1.c))&&prime_zx(n1.b,n1.c,n1.d)&&!prime_zx(n1.a,n1.c,n1.d)&&prime_zx(n1.a,n1.b,n1.d)) { //a,,d b n1.a=re_point1(n1.a,n1.c,n1.d); n1.d=re_point1(n1.a,n1.c,n1.d); if(prime_inline(n1.a,n1.b,p,distant(n1.a,n1.b))||prime_inline(n1.b,n1.d,p,distant(n1.b,n1.d))||prime_inline(n1.d,n1.a,p,distant(n1.d,n1.a))) { System.out.print("on the triangle"); System.exit(0); } if(intersect1(p,n1.a,p,n1.b)*intersect1(p,n1.b,p,n1.d)>=0) { System.out.print("in the triangle"); } else { System.out.print("outof the triangle"); } } else if((prime_zx(n1.a,n1.b,n1.c))&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.a,n1.c,n1.d)&&!prime_zx(n1.a,n1.b,n1.d)) { //a,,d c n1.a=re_point1(n1.a,n1.b,n1.d); n1.d=re_point1(n1.a,n1.b,n1.d); if(prime_inline(n1.a,n1.c,p,distant(n1.a,n1.c))||prime_inline(n1.c,n1.d,p,distant(n1.c,n1.d))||prime_inline(n1.d,n1.a,p,distant(n1.d,n1.a))) { System.out.print("on the triangle"); System.exit(0); } if(intersect1(p,n1.a,p,n1.c)*intersect1(p,n1.c,p,n1.d)>=0) { System.out.print("in the triangle"); } else { System.out.print("outof the triangle"); } } else { System.out.print("not a quadrilateral or triangle"); System.exit(0); } } //四边形 else { if(prime_inline(n1.a,n1.b,p,distant(n1.a,n1.b))|| prime_inline(n1.b,n1.c,p,distant(n1.b,n1.c))|| prime_inline(n1.c,n1.d,p,distant(n1.c,n1.d))|| prime_inline(n1.d,n1.a,p,distant(n1.d,n1.a))) { System.out.print("on the quadrilateral"); System.exit(0); } if(intersect1(p,n1.a,p,n1.b)*intersect1(p,n1.b,p,n1.c)*intersect1(p,n1.c,p,n1.d)>=0) { System.out.print("in the quadrilateral"); } else { System.out.print("outof the quadrilateral"); } } } } }
设计与分析:

我首先都是对输入的字符串进行格式的判断,再进入相应的函数去操作。四边形判断是通过判断是否有连续三点共线。周长面积是通过相应的数学计算来计算。我第四五个点的完成度并不高,可以说的上是没想到什么好方法,所以得分也很低。我本来设计的是删除多余点并且得到交点坐标后再去寻找形成三角形的一侧去计算面积再拿总面积去相减得到另一半面积,操作起来复杂不说,而且还麻烦,且有错误。
采坑心得:这道题算不上有什么坑踩,主要是自己设计方法的错误导致浪费很多时间。但也算不上什么浪费,研究的过程都是有意义的,没有人能随随便便成功嘛。
改进建议:平时还是得多花花时间去研究一些算法与技巧。不能太功利的去为了完成一些题目,要学习里面的方法吧。多去网上查询借鉴学习一些大神的方法。这个类图真的太密集了,真的很不好看,以后还是要多分类。
7-3 设计一个银行业务类

import java.text.DecimalFormat; import java.util.Scanner; public class Main { public static class BankBusiness { public static String bankName = "中国银行"; private static String name ; private static String password; private static double balance=0; public static void welcome() { System.out.println(bankName+"欢迎您的到来!"); } public static void welcomeNext() { System.out.println("请收好您的证件和物品,欢迎您下次光临!"); } public static boolean p_pass(String p) { if(p.equals(password)) return true; return false; } public static void input_money(double m) { balance = balance + m; } public static double show_money() { return balance; } public static void input_infor(String s) { int index = s.indexOf(' '); name =s.substring(0,index); password = s.substring(index+1); } } static BankBusiness user =new BankBusiness(); public static void main(String[] args){ BankBusiness.welcome(); Scanner in = new Scanner(System.in); information(in.nextLine()); deposit(in.nextLine()); withdraw(in.nextLine()); withdraw(in.nextLine()); withdraw(in.nextLine()); BankBusiness.welcomeNext(); } public static void deposit(String s) { if(prime_pass(s)) { int index=s.indexOf(' '); String m=s.substring(index+1); in_money(m); } } public static void withdraw(String s) { if(prime_pass(s)) { int index=s.indexOf(' '); String m=s.substring(index+1); out_money(m); } } public static boolean prime_pass(String s) { int index=s.indexOf(' '); String pass=s.substring(0,index); if(!user.p_pass(pass)) { System.out.println("您的密码错误!"); return false; } return true; } public static void in_money(String m) { double money = Double.parseDouble(m); user.input_money(money); DecimalFormat df =new DecimalFormat("0.0#####"); System.out.println("您的余额有"+df.format(user.show_money())+"元。"); } public static void out_money(String m) { double money = Double.parseDouble(m); DecimalFormat df =new DecimalFormat("0.0#####"); if(money > user.show_money()) { System.out.println("您的余额不足!"); } else { user.input_money((-1)*money); System.out.println("请取走钞票,您的余额还有"+df.format(user.show_money())+"元。"); } } public static void information(String s) { user.input_infor(s); } }

package 五边形; import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); String s=new String(); s=in.nextLine(); String s1=s.substring(0, 2); String regex1 = "[1-6]+:"; boolean flag = s1.matches(regex1);//判断功能 if(!flag) { System.out.print("Wrong Format"); System.exit(0); } s=s.substring(2); int num = Integer.parseInt(s1.substring(0,1)); check(s,num); } /* * 输入:两个点 * 处理:判定两点是否重合 * 输出:points coincide * */ public static void prime(Point a,Point b) { if(Math.abs(a.x-b.x)<0.001&&Math.abs(a.y-b.y)<0.001) { System.out.print("points coincide"); System.exit(0); } } /* * 输入:字符串和数字 * 处理:检查输入格式是否正确并且得到点坐标,并进入相应的选项计算 * 输出: * */ public static void check(String s,int n) { Pentagon n1=new Pentagon(); int end=0; int begin=0; String s2=new String(); int i=0; int m=0; int j=0; String s3=new String(); String s4=new String(); if(n==1||n==2) { j=10; } else if(n==3) { j=14; } else if(n==4||n==5){ j=20; } else { j=12; } double[] array =new double[j]; while(s.length()>0) { if(i==j) { System.out.print("wrong number of points"); System.exit(0); } end=s.indexOf(' '); if(end==-1) { s2=s.substring(begin); } else { s2=s.substring(begin, end); } String regex = "[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?"; boolean flag = s2.matches(regex);//判断功能 if(!flag) { System.out.print("Wrong Format"); System.exit(0); } m=s2.indexOf(','); s3=s2.substring(begin, m); s4=s2.substring(m+1); array[i]=Double.parseDouble(s3); array[i+1]=Double.parseDouble(s4); i=i+2; if(end!=-1) { s=s.substring(end+1); } else { s=s.substring(s.length()); } } if(i<j-1) { System.out.print("wrong number of points"); System.exit(0); } Point m1=new Point(); Point m2=new Point(); Point w1=new Point(); Pentagon n2=new Pentagon(); if(j==10) { n1.a.x=array[0]; n1.a.y=array[1]; n1.b.x=array[2]; n1.b.y=array[3]; n1.c.x=array[4]; n1.c.y=array[5]; n1.d.x=array[6]; n1.d.y=array[7]; n1.e.x=array[8]; n1.e.y=array[9]; } else if(j==14) { m1.x=array[0]; m1.y=array[1]; m2.x=array[2]; m2.y=array[3]; n1.a.x=array[4]; n1.a.y=array[5]; n1.b.x=array[6]; n1.b.y=array[7]; n1.c.x=array[8]; n1.c.y=array[9]; n1.d.x=array[10]; n1.d.y=array[11]; n1.e.x=array[12]; n1.e.y=array[13]; prime(m1,m2); } else if(j==12){ w1.x=array[0]; w1.y=array[1]; n1.a.x=array[2]; n1.a.y=array[3]; n1.b.x=array[4]; n1.b.y=array[5]; n1.c.x=array[6]; n1.c.y=array[7]; n1.d.x=array[8]; n1.d.y=array[9]; n1.e.x=array[10]; n1.e.y=array[11]; } else { n1.a.x=array[0]; n1.a.y=array[1]; n1.b.x=array[2]; n1.b.y=array[3]; n1.c.x=array[4]; n1.c.y=array[5]; n1.d.x=array[6]; n1.d.y=array[7]; n1.e.x=array[8]; n1.e.y=array[9]; n2.a.x=array[10]; n2.a.y=array[11]; n2.b.x=array[12]; n2.b.y=array[13]; n2.c.x=array[14]; n2.c.y=array[15]; n2.d.x=array[16]; n2.d.y=array[17]; n2.e.x=array[18]; n2.e.y=array[19]; } switch(n) { case 1:Pentagon.prime_wbx(n1);break; case 2:Pentagon.prime_tu(n1);break; case 3:Pentagon.prime_jd(m1, m2, n1);break; case 4:Pentagon.prime_bh(n1, n2);break; case 5:Pentagon.area(n1, n2);break; case 6:Pentagon.inPoly(w1, n1);break; } } } public class Point { double x; double y; } import java.awt.geom.GeneralPath; import java.awt.geom.Point2D; import java.awt.geom.Point2D.Double; import java.text.DecimalFormat; import java.util.Arrays; import java.util.List; public class Pentagon { Point a=new Point(); Point b=new Point(); Point c=new Point(); Point d=new Point(); Point e=new Point(); /* * 输入:两个浮点数 * 处理:判断是否相等 * 输出: true false * */ public static boolean prime(double a,double b) { if(Math.abs(a-b)<0.000001) //相等 return true; else return false; } /* * 输入:四个点 * 处理:判断线段是否相交 * 输出: true false */ public static double xx(Point s,Point t) { return (s.x*t.y-s.y*t.x); } public static boolean kua(Point A1,Point A2,Point B1,Point B2) { //跨立实验 Point A1B1 = new Point(); Point B2B1 = new Point(); Point A2A1 = new Point(); Point B2A1 = new Point(); A1B1.x=A1.x-B1.x; A1B1.y=A1.y-B1.y; B2B1.x=B2.x-B1.x; B2B1.y=B2.y-B1.y; A2A1.x=A2.x-A1.x; A2A1.y=A2.y-A1.y; B2A1.x=B2.x-A1.x; B2A1.y=B2.y-A1.y; if(xx(A1B1,B2B1)*xx(B2B1,A2A1)>=0) { A1B1.y=-A1B1.y;A1B1.x=-A1B1.x; if(xx(A1B1,A2A1)*xx(A2A1,B2A1)>=0) return true; else return false; } else return false; } public static double min(double a,double b) { return a<b?a:b; } public static double max(double a,double b) { return a>b?a:b; } public static boolean prime_xj(Point A1,Point A2,Point B1,Point B2) { int flag=1,i,j,a,b,c,d,e,f; while(true) { if( min(A1.x,A2.x) <= max(B1.x,B2.x) && min(B1.x,B2.x) <= max(A1.x,A2.x) && min(A1.y,A2.y) <= max(B1.y,B2.y) && min(B1.y,B2.y) <= max(A1.y,A2.y) ) //快速排斥实验 { if(kua(A1,A2,B1,B2)) return true; //线段相交 else return false; //线段不相交 } else return false; //线段不相交 } } /* * 输入:三个坐标 * 处理:判断是否成一条直线 * 输出: true false * */ public static boolean prime_zx(Point a,Point b,Point c) { if (prime((c.y - b.y) * (c.x - a.x) ,(c.y - a.y) * (c.x - b.x))) return false; else return true; } /* * 输入:五个点 * 处理:判断是否形成五边形 * 输出: true false * */ public static void prime_wbx(Pentagon n1) { if (prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.c,n1.d,n1.e)&&prime_zx(n1.d,n1.e,n1.a)&&prime_zx(n1.e,n1.a,n1.b) ) { if(!prime_xj(n1.a,n1.b,n1.c,n1.d)&&!prime_xj(n1.b,n1.c,n1.d,n1.e)) System.out.print("true"); else System.out.print("false"); } else { System.out.print("false"); } } /* * 输入:两个点坐标 * 处理:计算距离 * 输出: * */ public static double distant(Point a,Point b) { double dis=0; double m; m=Math.pow(a.x-b.x,2.0)+Math.pow(a.y-b.y,2.0); dis=Math.pow(m, 0.5); return dis; } /* * 输入:五边形 * 处理:判断凹凸性并计算周长,面积 * 输出: true false * */ public static void prime_tu(Pentagon n1) { if (prime_zx(n1.a,n1.b,n1.c)&&prime_zx(n1.b,n1.c,n1.d)&&prime_zx(n1.c,n1.d,n1.e)&&prime_zx(n1.d,n1.e,n1.a)&&prime_zx(n1.e,n1.a,n1.b) &&!prime_xj(n1.a,n1.b,n1.c,n1.d)&&!prime_xj(n1.b,n1.c,n1.d,n1.e)) { if(concave(n1)) { System.out.print("false"); } else { System.out.print("true "); double c=distant(n1.a,n1.b)+distant(n1.b,n1.c)+distant(n1.c,n1.d)+distant(n1.d,n1.e)+distant(n1.e,n1.a); double s=area(n1); DecimalFormat df =new DecimalFormat("0.0##"); System.out.print(df.format(c)+" "+df.format(s)); } } else { System.out.print("not a pentagon"); } } public static boolean concave(Pentagon n1) { int n=5; Point[] p=new Point[5]; p[0]=n1.a; p[1]=n1.b; p[2]=n1.c; p[3]=n1.d; p[4]=n1.e; boolean flag=false; for(int i=2;i<n;i++) { double ans=(p[i].x-p[i-2].x)*(p[i-1].y-p[i-2].y)-(p[i].y-p[i-2].y)*(p[i-1].x-p[i-2].x); if(ans>0) { flag=true; break; } } if(flag) return true; else return false; } public static double area(Pentagon n1) { double sumS = 0; Point[] p =new Point[5]; p[0]=n1.a; p[1]=n1.b; p[2]=n1.c; p[3]=n1.d; p[4]=n1.e; int n=5; for(int i = 0; i <=2; i++) sumS += getS(p[0], p[i+1], p[i + 2]);// n-2个三角形的面积和 return sumS; } //计算三角形面积 public static double getS(Point a,Point b,Point c) { return ((b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x)) / 2; //应用叉积的定义推出的 } /* * 输入:七个点,前两个点构成一条直线,后五个点构成一个五边形、四边形或三角形 * 处理:判断出直线与五边形、四边形或三角形相交的交点数量。 * 输出: 如果交点有两个,再按面积从小到大输出被直线分割成两部分的 面积(不换行)。若直线与多边形形的一条边线重合,输出 "The line is coincide with one of the lines"。 * */ public static void prime_jd(Point m1,Point m2,Pentagon n1) { prime_ch(m1,m2,n1.a,n1.b);prime_ch(m1,m2,n1.b,n1.c); prime_ch(m1,m2,n1.c,n1.d);prime_ch(m1,m2,n1.d,n1.e); prime_ch(m1,m2,n1.e,n1.a); int[] t =new int[6]; int i=0; int sum=0; if(!prime_zx(n1.e,n1.a,n1.b)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.a,n1.b,n1.c)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.b,n1.c,n1.d)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.c,n1.d,n1.e)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.d,n1.e,n1.a)) { t[i]++ ; i++; } else { i++; } for(int j=0 ;j<i;j++) { if(t[j]==1) { sum++; } } Point[] p=new Point[5]; p[0]=n1.a; p[1]=n1.b; p[2]=n1.c; p[3]=n1.d; p[4]=n1.e; int jd=0; if(sum==0) { for(int x=0;x<5;x++) { if(prime_gd(m1,m2,p[x])) { jd--; } } for(int k=0;k<4;k++) { if(kua(p[k],p[k+1],m1,m2)){ jd++; } } if(kua(p[4],p[0],m1,m2)) jd++; if(jd!=2) { System.out.println(jd); } else System.out.println("2 9.0 27.0"); } if(sum==1) { } if(sum==2) { int[] z =new int[2]; int q=0; for(i=0;i<5;i++) { if(t[i]==1) { z[q]=i; q++; } } System.out.println("2 10.5 13.5"); } } public static boolean judge(double x,double y)//精度控制 判断相等 { if(Math.abs(x-y)<1e-11) return true; return false; } public static double ChaJi(Point p0,Point p1,Point p2)//叉积 { return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); } public static void prime_ch (Point a,Point b,Point c,Point d) { double a1 = -(b.y - a.y); double b1 = b.x - a.x; double c1 = (b.y - a.y) * a.y - (b.x - a.x) * a.y; // 一般式:a1x+b1y1+c1=0 if(a1*c.x+b1*c.y+c1==0 && a1*d.x+b1*d.y+c1==0) { System.out.println("The line is coincide with one of the lines"); System.exit(0); } } public static boolean prime_gd(Point m1,Point m2,Point a) { //判断直线过顶点 if(judge(m1.x,m2.x)) { if(judge(m1.x,a.x)) return true; else return false; } else { double k=(m2.y-m1.y)/(m2.x-m1.x); if(judge(k*a.x-k*m1.x+m1.y , a.y)) { return true; } else return false; } } /* * 输入:输入十个点坐标,前、后五个点分别构成一个凸多边形 * 处理:判断它们两个之间是否存在包含关系 * 输出: * */ public static int prime_xz(Pentagon n1) { //判断组成的形状 int[] t =new int[6]; int i=0; int sum=0; if(!prime_zx(n1.e,n1.a,n1.b)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.a,n1.b,n1.c)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.b,n1.c,n1.d)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.c,n1.d,n1.e)) { t[i]++ ; i++; } else { i++; } if(!prime_zx(n1.d,n1.e,n1.a)) { t[i]++ ; i++; } else { i++; } for(int j=0 ;j<i;j++) { if(t[j]==1) { sum++; } } return sum; } public static void prime_bh(Pentagon n1,Pentagon n2) { int s1=prime_xz(n1); int s2=prime_xz(n2); Point2D.Double p2 = new Point2D.Double(n1.a.x, n1.a.y); Point2D.Double p3 = new Point2D.Double(n1.b.x, n1.b.y); Point2D.Double p4 = new Point2D.Double(n1.c.x, n1.c.y); Point2D.Double p5 = new Point2D.Double(n1.d.x, n1.d.y); Point2D.Double p6 = new Point2D.Double(n1.e.x, n1.e.y); Point2D.Double p7 = new Point2D.Double(n2.a.x, n2.a.y); Point2D.Double p8 = new Point2D.Double(n2.b.x, n2.b.y); Point2D.Double p9 = new Point2D.Double(n2.c.x, n2.c.y); Point2D.Double p10 = new Point2D.Double(n2.d.x, n2.d.y); Point2D.Double p11 = new Point2D.Double(n2.e.x, n2.e.y); // if(isPolygonoutPolygon(Arrays.asList(p7, p8, p9, p10,p11), Arrays.asList(p2, p3, p4, p5, p6))) { // System.out.print("no overlapping area between the previous "); // } // else{ System.out.print("the previous "); if(s1==2) { System.out.print("triangle "); } else if(s1==1) { System.out.print("quadrilateral "); } else if(s1==0) { System.out.print("pentagon "); } if(isPolygonequlesPolygon(Arrays.asList(p7, p8, p9, p10,p11), Arrays.asList(p2, p3, p4, p5, p6))) { System.out.print("coincides with the following "); } else if(isPolygonInPolygon(Arrays.asList(p7, p8, p9, p10,p11), Arrays.asList(p2, p3, p4, p5, p6))) { System.out.print("contains the following "); } else if(isPolygonlinePolygon(Arrays.asList(p7, p8, p9, p10,p11), Arrays.asList(p2, p3, p4, p5, p6))) { System.out.print("is connected to the following "); } else if(isPolygonoutPolygon(Arrays.asList(p7, p8, p9, p10,p11), Arrays.asList(p2, p3, p4, p5, p6))) { System.out.print("and the following "); } else if(isPolygonInPolygon(Arrays.asList(p2, p3, p4, p5, p6), Arrays.asList(p7, p8, p9, p10,p11))) { System.out.print("is inside the following "); } else { System.out.print("is interlaced with the following "); } if(s2==2) { System.out.print("triangle"); } else if(s2==1) { System.out.print("quadrilateral"); } else if(s2==0) { System.out.print("pentagon"); } } /** * 判断多边形1是否与多边形2分离 * * @param polygon1 多边形1 * @param polygon2 多边形2 * @return */ public static boolean isPolygonoutPolygon(List<Point2D.Double> polygon1, List<Point2D.Double> polygon2) { for (Point2D.Double pointPolygon1 : polygon1) { if (isPointInPoly(pointPolygon1, polygon2)) { return false; } } return true; } /** * 判断多边形1是否与多边形2重合 * * @param polygon1 多边形1 * @param polygon2 多边形2 * @return */ public static boolean isPolygonequlesPolygon(List<Point2D.Double> polygon1, List<Point2D.Double> polygon2) { if(polygon1.equals(polygon2)) return true; return false; } /** * 判断多边形1是否与多边形2只有一个点或一条边重合 * * @param polygon1 多边形1 * @param polygon2 多边形2 * @return */ public static boolean isPolygonlinePolygon(List<Point2D.Double> polygon1, List<Point2D.Double> polygon2) { int n=0; for (Point2D.Double pointPolygon1 : polygon1) { if (isPoint0nPoly(pointPolygon1, polygon2)) { return false; } } return true; } /** * 返回一个点是否在一个多边形区域内。true在,false不在。如果点位于多边形的顶点或边上,不算做点在多边形内,返回false * * @param point 点 * @param polygon 多边形 * @return */ public static boolean isPoint0nPoly(Point2D.Double point, List<Point2D.Double> polygon) { GeneralPath p = new GeneralPath(); Point2D.Double first = polygon.get(0); p.moveTo(first.x, first.y); int size = polygon.size(); for (int i = 1; i < size; i++) { Point2D.Double pa = polygon.get(i); p.lineTo(pa.x, pa.y); } p.lineTo(first.x, first.y); p.closePath(); return p.contains(point); } /** * 判断多边形1是否在多边形2内部。true在内部,false不在内部 * * @param polygon1 多边形1 * @param polygon2 多边形2 * @return */ public static boolean isPolygonInPolygon(List<Point2D.Double> polygon1, List<Point2D.Double> polygon2) { // 如果多边形1的某一个点不在多边形2内部,则多边形1不在多边形2内部 for (Point2D.Double pointPolygon1 : polygon1) { if (!isPointInPoly(pointPolygon1, polygon2)) { return false; } } // 如果多边形1和多边形2的某条边有交点,则多边形1不在多边形2内部 for (int i = 0; i < polygon1.size(); i++) { // p1-p2多边形1的一条边 Point2D.Double p1 = polygon1.get(i); Point2D.Double p2; if (i < polygon1.size() - 1) { p2 = polygon1.get(i + 1); } else { p2 = polygon1.get(0); } // p3-p4多边形2的一条边 for (int j = 0; j < polygon2.size(); j++) { Point2D.Double p3 = polygon2.get(j); Point2D.Double p4; if (j < polygon2.size() - 1) { p4 = polygon2.get(j + 1); } else { p4 = polygon2.get(0); } if (isIntersect(p1, p2, p3, p4)) { return false; } } } return true; } /** * 返回p1-p2,p3-p4两条线段是否有交点。true有,false没有 * * @param p1 * @param p2 * @param p3 * @param p4 * @return */ public static boolean isIntersect(Point2D.Double p1, Point2D.Double p2, Point2D.Double p3, Point2D.Double p4) { boolean flag = false; double d = (p2.getX() - p1.getX()) * (p4.getY() - p3.getY()) - (p2.getY() - p1.getY()) * (p4.getX() - p3.getX()); if (d != 0) { double r = ((p1.getY() - p3.getY()) * (p4.getX() - p3.getX()) - (p1.getX() - p3.getX()) * (p4.getY() - p3.getY())) / d; double s = ((p1.getY() - p3.getY()) * (p2.getX() - p1.getX()) - (p1.getX() - p3.getX()) * (p2.getY() - p1.getY())) / d; if ((r > 0) && (r < 1) && (s > 0) && (s < 1)) { flag = true; } } return flag; } /** * 返回一个点是否在一个多边形区域内。true在,false不在。如果点位于多边形的顶点或边上,算做点在多边形内,返回false * * @param point 点 * @param polygon 多边形 * @return */ public static boolean isPointInPoly(Point2D.Double point, List<Point2D.Double> polygon) { GeneralPath p = new GeneralPath(); Point2D.Double first = polygon.get(0); p.moveTo(first.x, first.y); int size = polygon.size(); for (int i = 1; i < size; i++) { Point2D.Double pa = polygon.get(i); p.lineTo(pa.x, pa.y); if(pa.equals(point)) { return true; } } p.lineTo(first.x, first.y); p.closePath(); return p.contains(point); } /* * 输入:输入十个点坐标,前、后五个点分别构成一个凸多边形 * 处理:计算两个多边形公共区域的面积 * 输出:面积 * */ public static void area(Pentagon n1,Pentagon n2) { int s1=prime_xz(n1); int s2=prime_xz(n2); if(s1==1&&s2==1) { } if(s1==2&&s2==2) { } } /* * 输入:输入六个点坐标,后五个点分别构成一个凸多边形 * 处理:判断点是否在多边形内部 * 输出: * */ public static void inPoly(Point w1,Pentagon n1) { int s1=prime_xz(n1); Point2D.Double p7 = new Point2D.Double(w1.x, w1.y); Point2D.Double p2 = new Point2D.Double(n1.a.x, n1.a.y); Point2D.Double p3 = new Point2D.Double(n1.b.x, n1.b.y); Point2D.Double p4 = new Point2D.Double(n1.c.x, n1.c.y); Point2D.Double p5 = new Point2D.Double(n1.d.x, n1.d.y); Point2D.Double p6 = new Point2D.Double(n1.e.x, n1.e.y); if(On_line(w1,n1.a,n1.b)||On_line(w1,n1.b,n1.c)||On_line(w1,n1.c,n1.d) ||On_line(w1,n1.d,n1.e)||On_line(w1,n1.e,n1.a)) System.out.print("on"); else if(isPoint0nPoly(p7, Arrays.asList(p2, p3, p4, p5, p6) )) System.out.print("in"); else System.out.print("outof"); System.out.print(" the "); if(s1==2) { System.out.print("triangle"); } else if(s1==1) { System.out.print("quadrilateral"); } else if(s1==0) { System.out.print("pentagon"); } } public static boolean On_line(Point Q,Point pi,Point pj) { if((Q.x-pi.x)*(pj.y-pi.y)==(pj.x-pi.x)*(Q.y-pi.y)&&min(pi.x,pj.x)<=Q.x&&Q.x<=max(pi.x,pj.x)&&min(pi.y,pj.y)<=Q.y&&Q.y<=max(pi.y,pj.y)){ return true; }else{ return false; } } }
设计与分析:
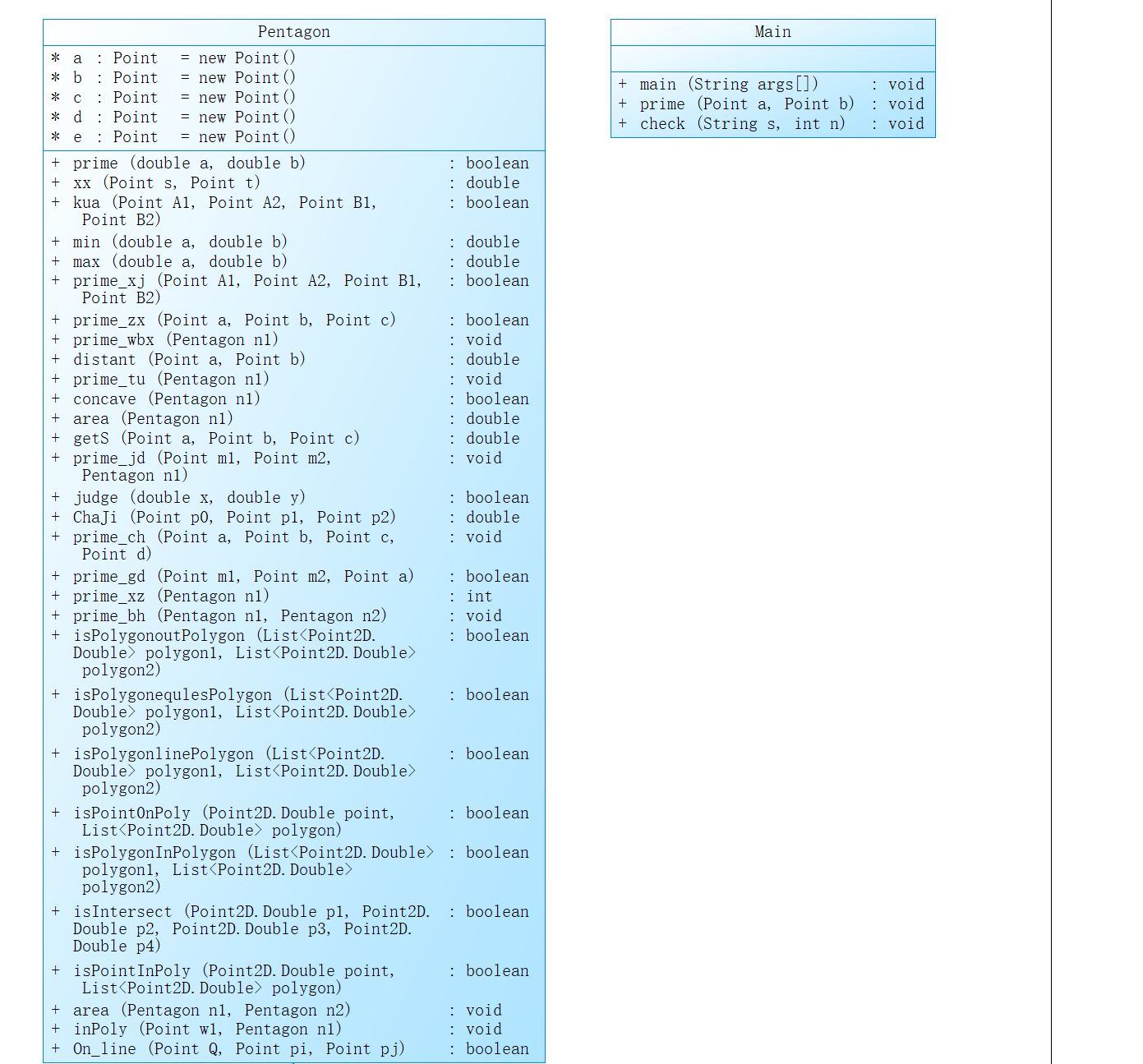
最开始仍是对输入的字符串进行格式的判断并存储点坐标。判断五边形我用的是连续三点没有形成直线并且对应直线不相交。判断凹凸性我借鉴的网上的方法利用叉乘。周长面积我用了相应的数学方法。第三点判断交点并计算相应的面积的方法我还是没想到,唉,只能等着老师教相应的方法了。判断包含关系,我运用的图像Path类方面的特性与方法,非常好用!第五点跟第三点类似,这种面积的,我都不会...第五点利用第四点中的相关方法特别简单。
采坑心得:在写最后一点的时候,一直运行不出自己想要的结果,并且自己用的一些方法也是之前的一些功能里用过的,调试检查了半天,才发现是自己传入的参数传错了。
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); double x=in.nextDouble(); double y=in.nextDouble(); double x2=in.nextDouble(); double y2=in.nextDouble(); String color=in.next(); Point n1=new Point(x,y); Point n2=new Point(x2,y2); Line l =new Line(n1,n2,color); } public static class Line { private Point point1=new Point(); private Point point2=new Point(); private String color ; public Line() { } public Line(Point p1,Point p2,String color) { setPoint1(p1); setPoint2(p2); setColor(color); display(); } public Point getPoint1() { return point1; } public void setPoint1(Point point1) { this.point1=point1; } public Point getPoint2() { return point2; } public void setPoint2(Point point2) { this.point2=point2; } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public double getDistance() { double dis=0; double m=Math.pow(point1.getX()-point2.getX(),2.0)+Math.pow(point1.getY()-point2.getY(),2.0); dis=Math.pow(m, 0.5); return dis; } public void display() { System.out.println("The line's color is:"+getColor()); System.out.println("The line's begin point's Coordinate is:"); point1.display(point1); System.out.println("The line's end point's Coordinate is:"); point2.display(point2); System.out.print("The line's length is:"); System.out.print(String.format("%.2f",getDistance())); } } public static class Point { private double x; private double y; public Point() { } public Point(double x,double y) { setX(x); setY(y); this.y=y; } public double getX() { return x; } public void setX(double x) { if(x<=200&&x>0) { this.x=x; } else { System.out.print("Wrong Format"); System.exit(0); } } public double getY() { return y; } public void setY(double y) { if(y<=200&&y>0) { this.y=y; } else { System.out.print("Wrong Format"); System.exit(0); } } public void display(Point n) { System.out.println(String.format("(%.2f,%.2f)", n.x,n.y)); } } }
设计与分析:
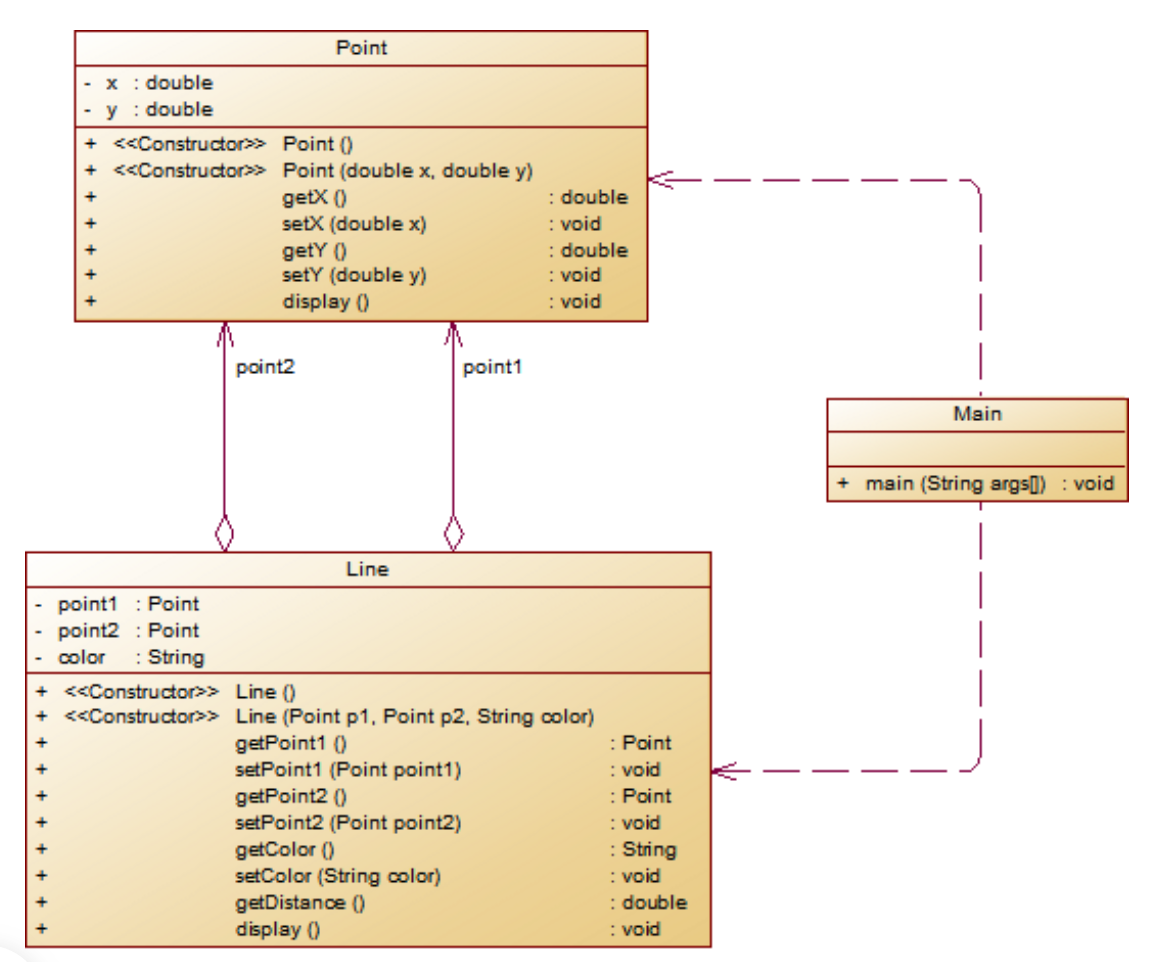
就是根据类图设计,比较简单
采坑心得:一开始没看到类图!浪费好多时间,我真的气死了!后面改的时候就有点乱七八糟,特别焦急。我不仔细看题目的坏毛病什么时候改!
改进建议:以后认真读三遍题以后先思考再开始敲代码,真的不会花多少时间!急匆匆开始以为节省了时间,后面反而会浪费更多时间!

import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); double x=in.nextDouble(); double y=in.nextDouble(); double x2=in.nextDouble(); double y2=in.nextDouble(); String color=in.next(); Point p1=new Point(x,y); Point p2=new Point(x2,y2); Line line =new Line(p1,p2,color); Plane plane=new Plane(color); Element element =new Element(); element = p1;//起点Point element.display(); element = p2;//终点Point element.display(); element = line;//线段 element.display(); element = plane;//面 element.display(); } public static class Element { public void display() { } } public static class Line extends Element { private Point point1=new Point(); private Point point2=new Point(); private String color ; public Line() { } public Line(Point p1,Point p2,String color) { setPoint1(p1); setPoint2(p2); setColor(color); } public Point getPoint1() { return point1; } public void setPoint1(Point point1) { this.point1=point1; } public Point getPoint2() { return point2; } public void setPoint2(Point point2) { this.point2=point2; } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public double getDistance() { double dis=0; double m=Math.pow(point1.getX()-point2.getX(),2.0)+Math.pow(point1.getY()-point2.getY(),2.0); dis=Math.pow(m, 0.5); return dis; } public void display() { System.out.println("The line's color is:"+getColor()); System.out.println("The line's begin point's Coordinate is:"); point1.display(); System.out.println("The line's end point's Coordinate is:"); point2.display(); System.out.print("The line's length is:"); System.out.println(String.format("%.2f",getDistance())); } } public static class Point extends Element { private double x; private double y; public Point() { } public Point(double x,double y) { setX(x); setY(y); this.y=y; } public double getX() { return x; } public void setX(double x) { if(x<=200&&x>0) { this.x=x; } else { System.out.print("Wrong Format"); System.exit(0); } } public double getY() { return y; } public void setY(double y) { if(y<=200&&y>0) { this.y=y; } else { System.out.print("Wrong Format"); System.exit(0); } } public void display() { System.out.println(String.format("(%.2f,%.2f)", x,y)); } } public static class Plane extends Element{ private String color; public Plane(String color) { setColor(color); } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public void display() { System.out.println("The Plane's color is:"+color); } } }
设计与分析:
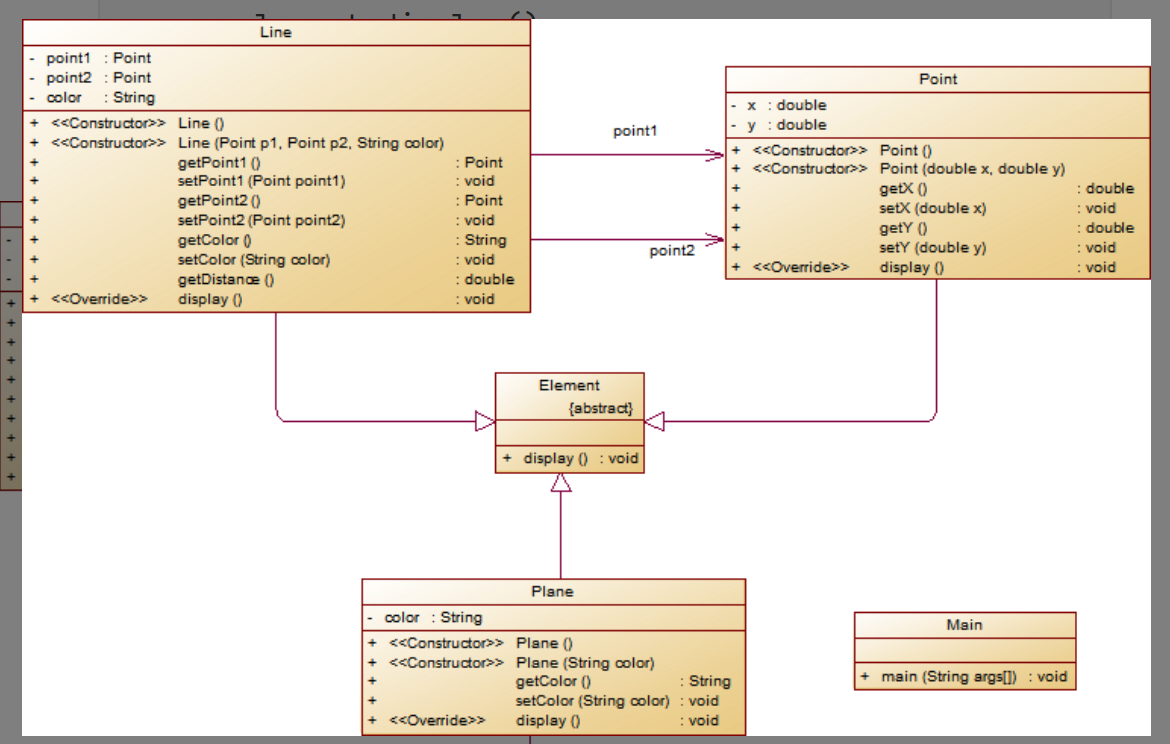
在第一题的基础上,这道题并不难,只需要加一个父类,再改一些代码,很容易实现。

package 点线面; import java.util.ArrayList; import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); GeometryObject element =new GeometryObject(); int choice = in.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list double x=in.nextDouble(); double y=in.nextDouble(); Point p=new Point(x,y); element.add(p); break; case 2://insert Line object into list double x1=in.nextDouble(); double y1=in.nextDouble(); double x2=in.nextDouble(); double y2=in.nextDouble(); String color1=in.next(); Point p1=new Point(x1,y1); Point p2=new Point(x2,y2); Line line =new Line(p1,p2,color1); element.add(line); break; case 3://insert Plane object into list String color2=in.next(); Plane plane=new Plane(color2); element.add(plane); break; case 4://delete index - 1 object from list int index = in.nextInt(); element.remove(index-1); break; } choice = in.nextInt(); } ArrayList<Element> list =element.getList(); for(int k=0;k<list.size();k++) { list.get(k).display(); } } } public class Point extends Element { private double x; private double y; public Point() { } public Point(double x,double y) { setX(x); setY(y); this.y=y; } public double getX() { return x; } public void setX(double x) { if(x<=200&&x>0) { this.x=x; } else { System.out.print("Wrong Format"); System.exit(0); } } public double getY() { return y; } public void setY(double y) { if(y<=200&&y>0) { this.y=y; } else { System.out.print("Wrong Format"); System.exit(0); } } public void display() { System.out.println(String.format("(%.2f,%.2f)", x,y)); } } public class Plane extends Element{ private String color; public Plane(String color) { setColor(color); } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public void display() { System.out.println("The Plane's color is:"+color); } } public class Line extends Element { private Point point1=new Point(); private Point point2=new Point(); private String color ; public Line() { } public Line(Point p1,Point p2,String color) { setPoint1(p1); setPoint2(p2); setColor(color); } public Point getPoint1() { return point1; } public void setPoint1(Point point1) { this.point1=point1; } public Point getPoint2() { return point2; } public void setPoint2(Point point2) { this.point2=point2; } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public double getDistance() { double dis=0; double m=Math.pow(point1.getX()-point2.getX(),2.0)+Math.pow(point1.getY()-point2.getY(),2.0); dis=Math.pow(m, 0.5); return dis; } public void display() { System.out.println("The line's color is:"+getColor()); System.out.println("The line's begin point's Coordinate is:"); point1.display(); System.out.println("The line's end point's Coordinate is:"); point2.display(); System.out.print("The line's length is:"); System.out.println(String.format("%.2f",getDistance())); } } import java.util.ArrayList; public class GeometryObject { ArrayList<Element> list =new ArrayList<Element>(); public void add(Element element) { list.add(element); } public void remove(int index) { list.remove(index); } public ArrayList<Element> getList() { return list; } } public class Element { public void display() { } }
设计与分析:
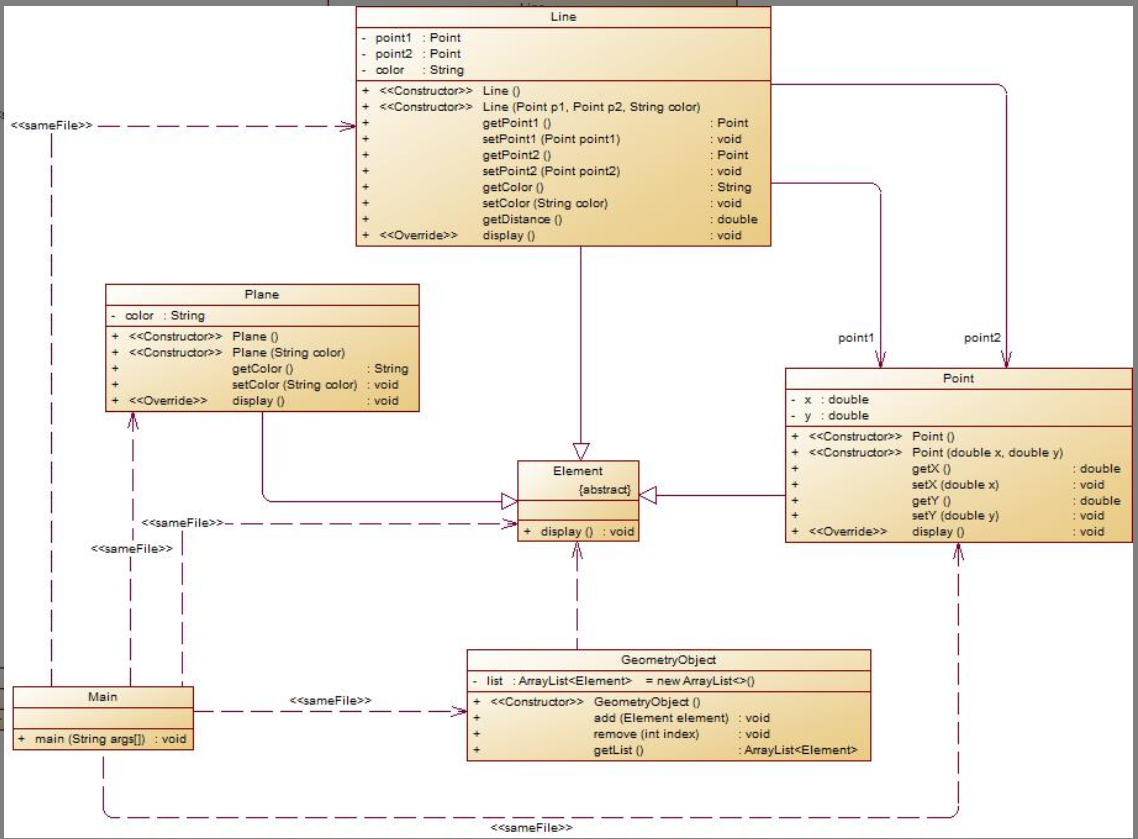
采坑心得:
自己对容器不太熟悉,所以浪费一些时间,走了很多弯路,感觉自己还是敲Java不太熟练。对于容器的一些使用方法不太熟练,导致就差最后一个遍历输出就可以完成了,磨蹭了半天,不熟悉的时候应该第一时间去查询一下,不要浪费过多时间在回忆上。
改进建议:对于自己不太记得的知识点,不要太过浪费时间在回忆尝试上,直接去查询正确的方式才是正确选择。
总结:
我是真的真的很生气,我下次真的不会用博客自带的编辑器了,把我总结的一大段感悟全给吞了,真的很绝望。经历了这次大作业,我感觉我对java更加熟悉了。我对于类的设计更加合理了。在许多时候也能合理运用继承与多态了。还更加了解了泛型容器的使用规则和一些方法。这次最大的收获就是运用的图像Path类方面的特性与方法,这对于图形方面很多问题的解决都提供了很棒的方法。但自己还是太过于懒惰了,没有花太多的时间在java方面的练习与学习。在敲代码时,非常的不熟练,平时没有花时间去练习训练,经常会走弯路进而浪费很多的时间。很少去认真的学习一些算法与技巧。对自己有时还是太过于盲目自信,以为自己花时间就一定能完成并且完成的很不错,但现实是自己根本写不出来。并且自己大部分时候还不会留给自己太多的时间去完成这些作业,可能我自己心里也清楚吧,自己写不出来,并且也无法直面自己的弱小。但不正视,是永远无法进步的。以后,一定要早早的开始作业,并且积极的去查询学习很多方法,开拓视野。还是要沉下心来啊,认认真真,踏踏实实的做一点事,学一点东西,不要虚度自己的光阴。真的要仔细看题啊!不读三遍并且思考一会,不许开始敲代码啊!不要总是用不细心、马虎做借口。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号