最大流dinic算法

最大流

前言

dinic算法是网络流中速度较快的算法，相比EK算法，dinic在稠密图中会更占优势。

什么是网络流

对于一张图 \(G = (V, E)\)，每条边都会有一个容量，从原点引入水流，水流要通过边流到汇点，水流不可以超过边的容量，而最大流就是求一种方案使得可以从流最多的水到达汇点。

当然，网络流肯定满足以下性质：
设 \(f(u, v)\) 为这条边的流量，\(c(u, v)\) 为这条边的限制

1. 容量限制：对于每条边，流经该边的流量不得超过该边的容量，即 \(0 \leq f(u, v) \leq c(u, v)\)
2. 流量守恒：除源汇点外，任意结点 \(u\) 的净流量为 \(0\)其中，我们定义 \(u\) 的净流量为 \(f(u) = \sum_{x \in V} f(u, x) - \sum_{x \in V} f(x, u)\)

dinic 求最大流

dinic的大体流程为：

1. 用 bfs 求出 \(G\) 中每个点的深度(Level Graph)
2. 用 dfs 在 bfs 所跑出来的图中，枚举一条从源点到汇点的路径\(P\)，求出 \(limit = Min(c \in P)\)，将路径上的每条边都减去 \(limit\)，并新建一条反边，权值为 \(limit\)/，为了可以撤销
3. 答案加上流量

这样说还是太抽象了，我们拿一个具体的图来说明:

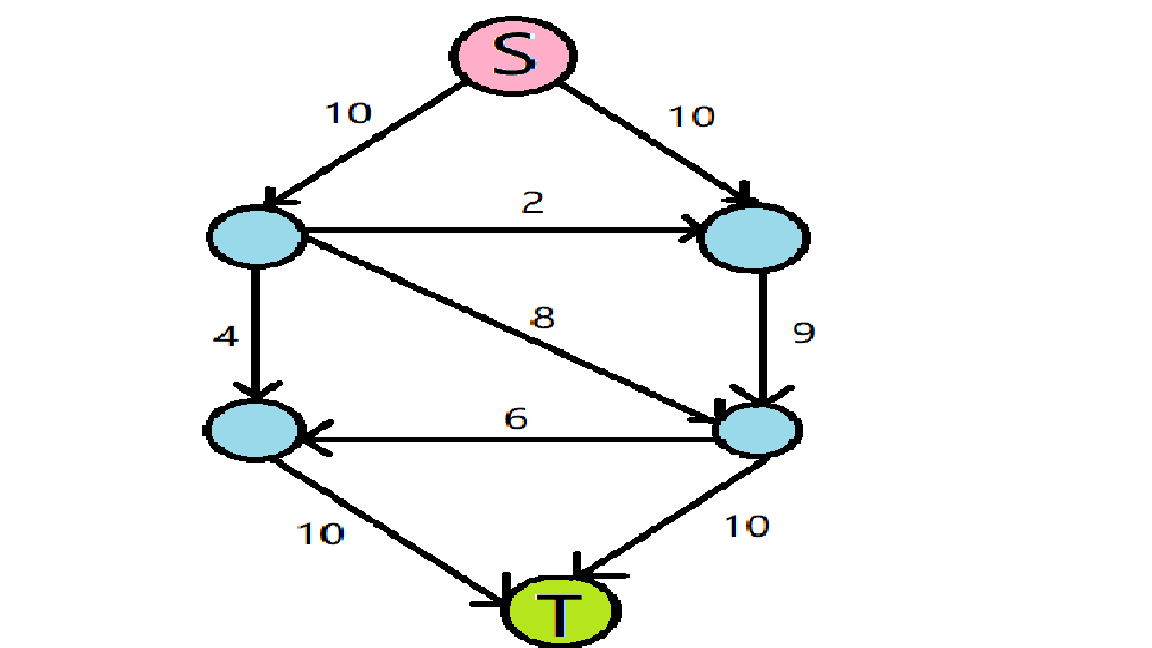
要求这张图的最大流，首先执行第一步，创建Level Graph，也就是从图中找到一个堵塞流，如下图：

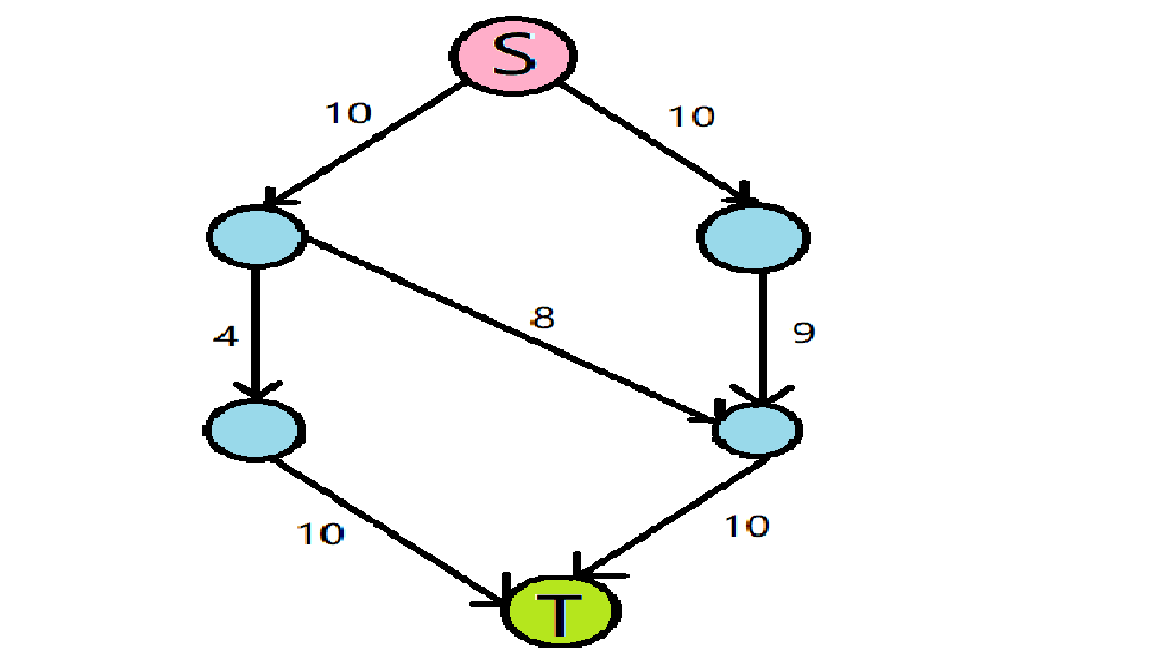
现在执行第二部操作，若有两个点有两条同样方向的边，我们可以相加合并，操作后如下图：

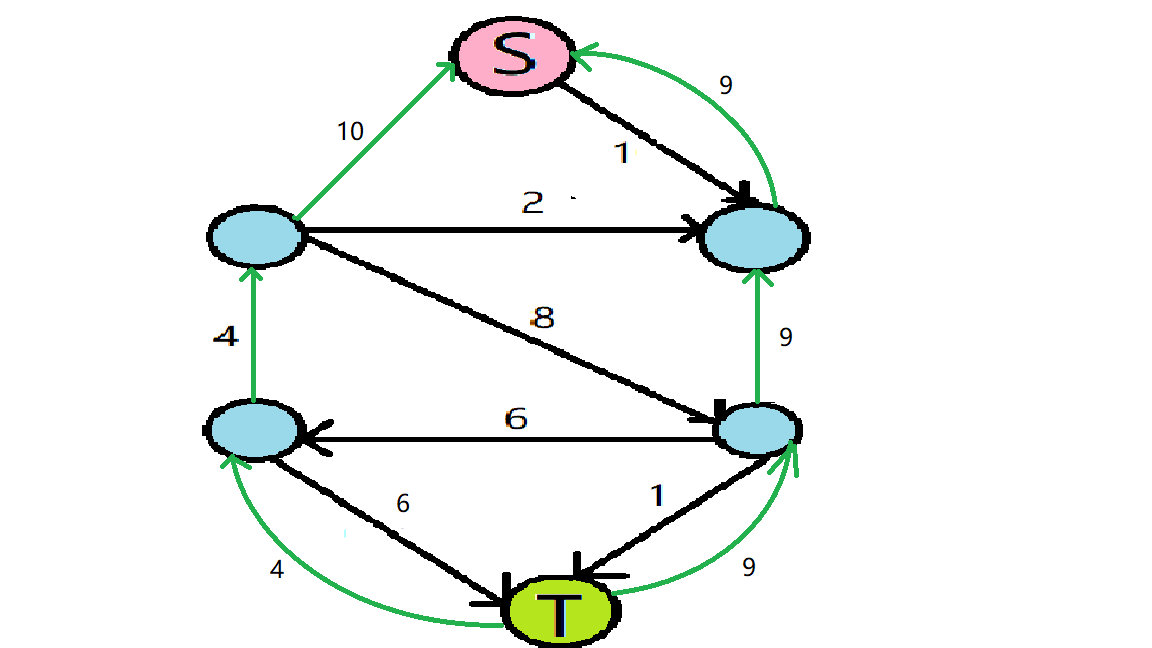
现在第一轮的过程结束了，开始第二轮，创建Level Graph:

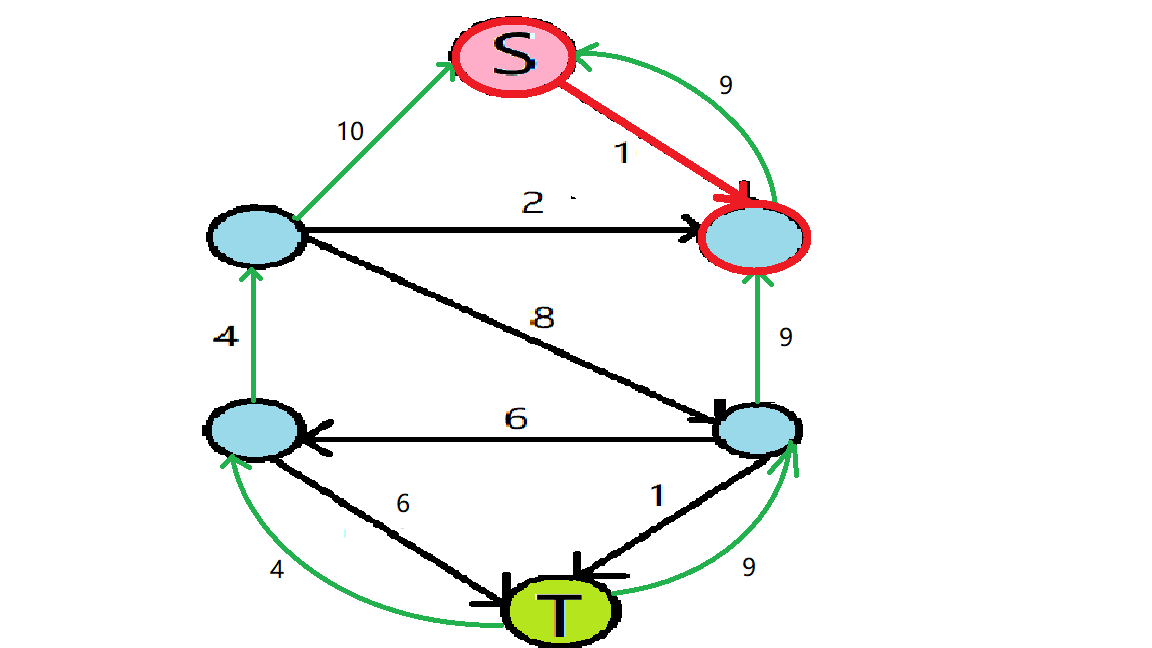
发现无法再次找到一条路径从 \(S\) 连到 \(T\)，所以就可以结束了。

代码实现

首先，声明一些变量：

• \(id\)：如果你用 vector 存图，就不能直接从 \(v\) 访问 \(u\)，所以要存一下 \(u\) 在 \(g[v]\) 中的下标
• \(bfs\)：创建 Level Graph，\(dep\) 为节点的深度
• \(dfs\)：实现 dinic 的第二、三步操作，其中 \(flow\) 为路径中的最小流量限制

struct Edge {
    int v, id, w；
};
vector<Edge> g[N];

void add(int x, int y, int w) {
    g[x].push_back({y, g[y].size(), w});
    g[y].push_back({x, g[x].size() - 1, 0}); // 注意这里反边的权值要设为0 ！！！不然输出方案时可能会错
}

bool bfs() {
	memset(dep, 0x3f, sizeof dep);
    queue<int> q;
    q.push(S);
    dep[S] = 1;
    while (q.size()) {
        int u = q.front(); q.pop();
        for (auto t : g[u]) {
            int v = t.v, w = t.w;
            if (dep[v] != 0x3f3f3f3f || !w) continue;
            dep[v] = dep[u] + 1;
            q.push(v);
        }
    }
    return dep[T] != 0x3f3f3f3f;
}

int dfs(int x, int flow) {
    if (x == T) return flow;
    int sum = 0;
    for (auto &t : g[x]) {
        int y = t.v, w = t.w, id = t.id;
        if (!w || dep[y] != dep[x] + 1) continue;
        int f = dfs(y, min(flow, w));
        if (!f) continue;
        sum += f;
        flow -= f;
        t.w -= f;
        g[y][id].w += f;
        if (!flow) break;
    }
    return sum;
}

void dinic() {
    while (bfs()) {
        ans += dfs(S, 0x3f3f3f3f);
    }
}

完结撒花！！！