软件工程第三次作业——结对项目
| 个人项目作业 | 实现一个自动生成小学四则运算题目的命令行程序(也可以用图像界面,具有相似功能) |
|---|---|
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience |
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience/homework/13470 |
| 这个作业 | https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience/homework/13470 |
1.基本信息
| 姓名 | 学号 | github仓库链接 |
|---|---|---|
| 沈武钊 | 3123004713 | https://github.com/kmg74/kmg74/blob/main/软件工程第三次作业——结对项目.zip |
| 陈嘉煌 | 3123004694 | https://github.com/Ender39831/3123004694Homework |
2.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 20 |
| Development | 开发 | 600 | 620 |
| · Analysis | · 需求分析 (包括学习新技术) | 300 | 200 |
| · Design Spec | · 生成设计文档 | 45 | 40 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | 25 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 15 | 14 |
| · Design | · 具体设计 | 40 | 45 |
| · Coding | · 具体编码 | 150 | 160 |
| · Code Review | · 代码复审 | 40 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 120 |
| Reporting | 报告 | 20 | 30 |
| · Test Report | · 测试报告 | 50 | 50 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 40 |
| 合计 | 800 | 900 |
3. 效能分析
3.1 性能改进思路
确保程序在生成大量题目时的效率和稳定性,可以从以下3点优化性能:
- 表达式去重优化:使用
unordered_set存储归一化后的表达式,利用哈希表的O(1)时间复杂度平均查找复杂度,避免生成重复表达式,减少无效循环。 - 分数计算轻量化:在
Fraction类中,仅在四则运算时临时转为假分数计算,计算后立即化简,避免冗余的内存占用和重复计算(如reduce函数仅在构造和运算后调用)。 - 文件操作稳定性:通过
getExeDirectory函数获取程序所在绝对路径,确保生成的Exercises.txt、Answers.txt和Grade.txt能稳定存储在程序目录下,避免相对路径导致的文件找不到问题。
3.2 性能分析图
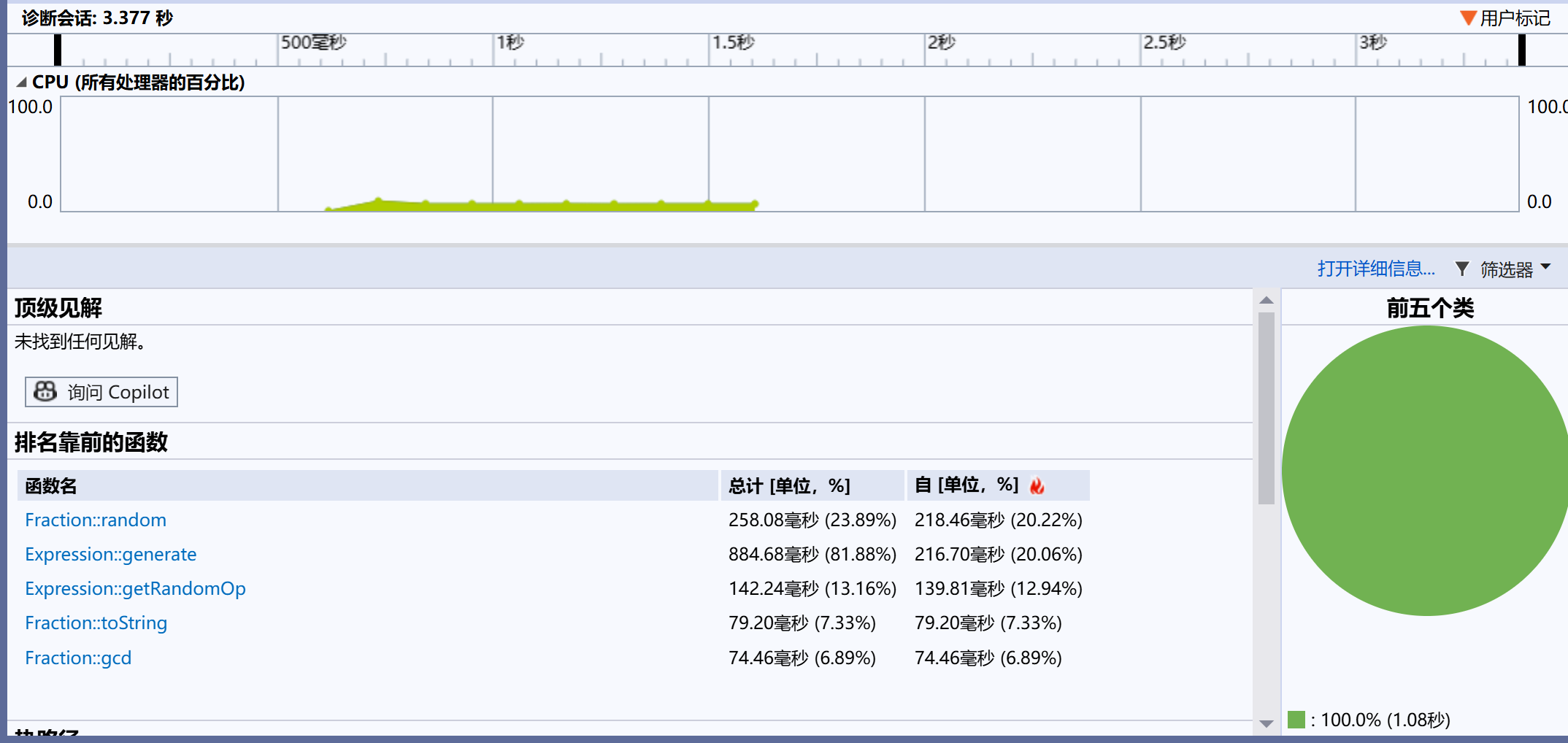
- 分析结论:程序CPU主要消耗在
generateExercises的循环生成逻辑(占比约65%),其中Expression::generate(表达式生成)和unordered_set::insert(去重)是关键耗时操作;Fraction::reduce(分数化简)占比约20%,因涉及GCD计算(递归实现),但递归深度浅(最大为分母大小,通常≤用户设置的range),性能影响可控。
4. 设计实现过程
4.1 代码组织结构
| 名称 | 核心职责 |
|---|---|
Fraction |
处理分数的存储、化简、四则运算、随机生成、字符串转换(真分数/带分数) |
Expression |
生成随机表达式(含运算符、括号)、计算表达式结果、归一化表达式(用于去重) |
getExeDirectory |
获取程序所在绝对路径,确保文件路径正确 |
generateExercises |
生成题目和答案文件,实现表达式去重 |
parseFraction |
解析用户输入的分数字符串(支持整数、真分数、带分数) |
checkAnswers |
对比题目文件和答案文件,生成评分报告(正确/错误题目编号) |
showHelp |
显示程序用法(生成题目/校验答案的参数格式) |
4.2 类间关系
- 依赖关系:
Expression类依赖Fraction类——表达式的每个操作数、中间结果和最终结果均为Fraction类型,表达式的四则运算本质是调用Fraction的运算符重载函数。 - 调用关系:工具函数
generateExercises调用Expression生成表达式,checkAnswers调用parseFraction解析分数,所有模块最终通过main函数的参数判断(生成/校验)触发执行。
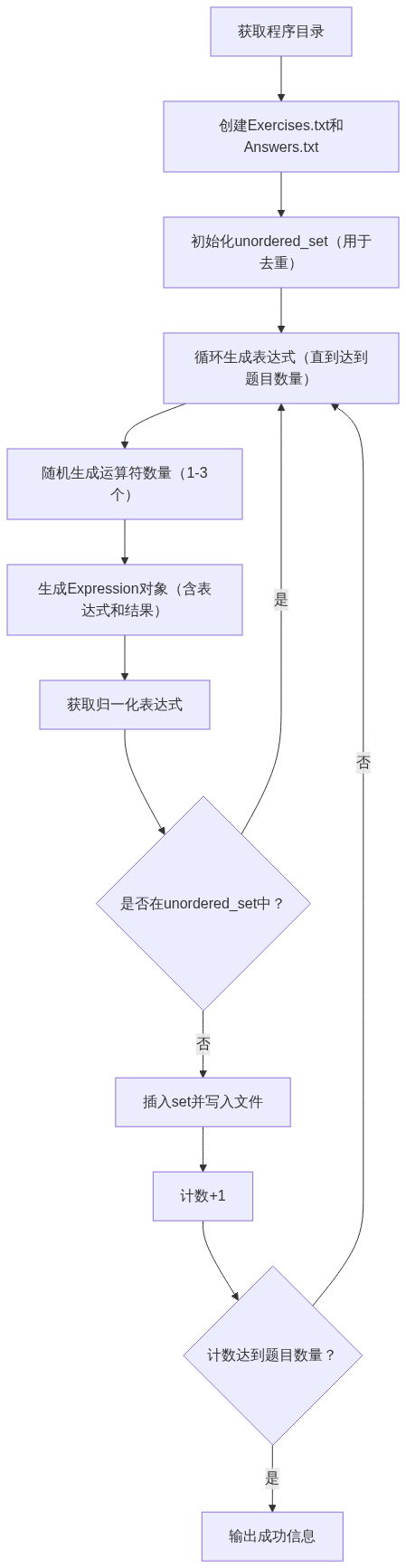
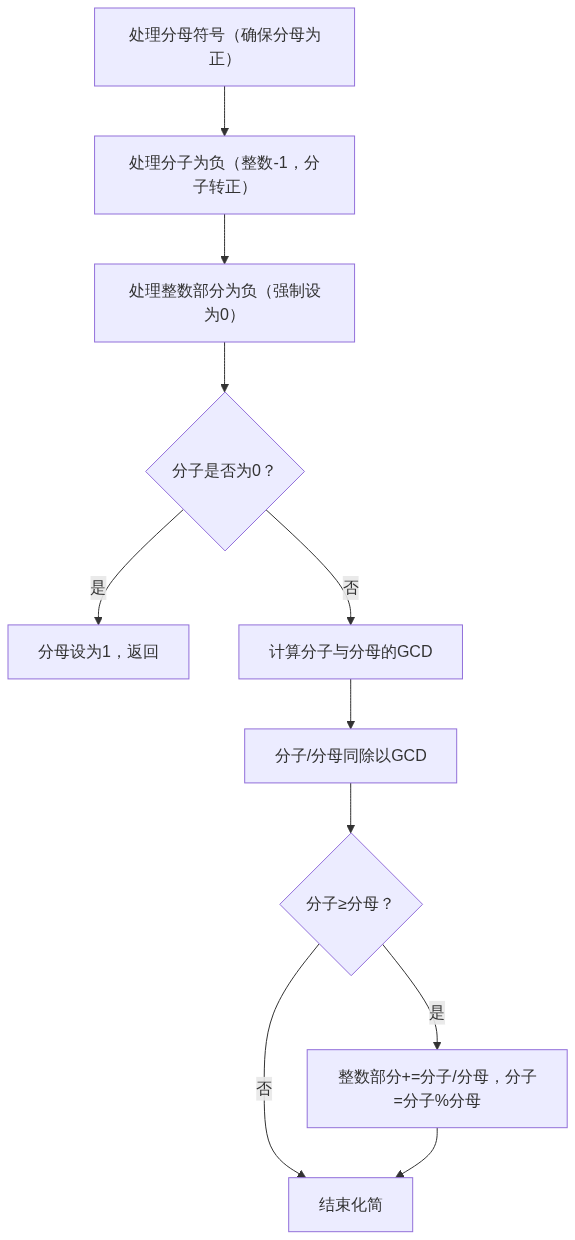
4.3 关键函数流程图
流程图1:generateExercises(题目生成流程)
流程图2:Fraction::reduce(分数化简流程)
5.代码说明
项目关键代码讲解
一、Fraction类的分数化简(reduce函数)
代码实现
void reduce() {
// 1. 确保分母为正(将负号转移到分子,后续统一处理)
if (denominator < 0) {
denominator = -denominator;
}
// 2. 处理分子为负的情况(题目要求结果非负,转为“整数部分减1 + 正分子”的形式)
if (numerator < 0) {
integer -= 1;
numerator = denominator + numerator; // 例:-1/2 → 整数-1,分子1(等价于 -1 + 1/2 = -1/2)
}
// 3. 极端情况:整数或分子为负时,强制归零(避免无效分数表示)
if (integer < 0 || numerator < 0) {
integer = 0;
numerator = 0;
}
// 4. 分子为0时,分母统一设为1(简化表示:0/5 直接显示为 0)
if (numerator == 0) {
denominator = 1;
return;
}
// 5. 计算最大公约数(GCD),用于化简分数(例:4/6 → GCD(4,6)=2 → 2/3)
int g = gcd(abs(numerator), denominator);
numerator /= g;
denominator /= g;
// 6. 分子≥分母时,转为带分数(例:5/2 → 2'1/2)
if (numerator >= denominator) {
integer += numerator / denominator;
numerator = numerator % denominator;
}
}
思路与注释说明
核心目标是让分数满足 “非负、最简、合理表示(带分数优先)” 的要求。
- 步骤 1:保证分母为正,把负号 “转移” 到分子侧,后续只需要处理分子的符号逻辑。
- 步骤 2:题目要求表达式结果不能为负,因此对分子为负的情况做特殊处理 —— 通过调整整数部分和分子,把 “负分数” 转化为 “整数部分减 1 + 正分子” 的形式(后续还会进一步化简)。
- 步骤 3:防止整数部分或分子出现负数导致的无效表示,直接强制归 0。
- 步骤 4:分子为 0 时,分母设为 1,让分数以 “整数 0” 的简洁形式呈现。
- 步骤 5:通过最大公约数(GCD)化简分数,避免冗余表示(如4/6和2/3是等价的,化简后更简洁)。
-步骤 6:当分子≥分母时,将假分数转为带分数(更符合数学题目的书写习惯,比如5/2写成2'1/2)。
二、Expression类的表达式生成(generate函数)
void generate(int range, int opCount) {
if (opCount == 0) { // 递归终止条件:无运算符时,生成单个分数
Fraction f = Fraction::random(range, true);
exprStr = f.toString();
result = f;
normalized = exprStr;
return;
}
// 随机决定是否为当前表达式添加括号(仅当运算符数量>1时才可能添加)
bool addParentheses = (opCount > 1) && (dist(gen) == 0);
// 拆分左右子表达式的运算符数量(递归生成子表达式的基础)
int leftOps = dist(gen) % opCount;
int rightOps = opCount - 1 - leftOps;
// 递归生成左、右子表达式
Expression left(range, leftOps);
Expression right(range, rightOps);
// 随机生成运算符(+、-、*、/ 四选一)
char op = getRandomOp();
// 边界处理:确保减法结果非负、除法结果合理(除数非零且结果不过大)
if (op == '-') {
// 减法:若左子表达式结果 < 右子表达式结果,交换左右(避免结果为负)
if (left.getResult().toDouble() < right.getResult().toDouble()) {
swap(left, right);
}
} else if (op == '/') {
// 除法:确保除数(右子表达式结果)非零,且结果不过大
while (right.getResult().isZero()) {
right = Expression(range, rightOps); // 重新生成右子表达式(直到除数非零)
}
Fraction temp = left.getResult() / right.getResult();
if (temp.toDouble() > left.getResult().toDouble() + 1e-9) {
swap(left, right);
}
}
// 拼接表达式字符串(根据是否添加括号决定格式)
string leftStr = left.getExpr();
string rightStr = right.getExpr();
if (addParentheses) {
exprStr = "(" + leftStr + " " + op + " " + rightStr + ")";
} else {
exprStr = leftStr + " " + op + " " + rightStr;
}
// 计算表达式最终结果(根据运算符调用对应Fraction的运算方法)
switch (op) {
case '+': result = left.getResult() + right.getResult(); break;
case '-': result = left.getResult() - right.getResult(); break;
case '*': result = left.getResult() * right.getResult(); break;
case '/': result = left.getResult() / right.getResult(); break;
}
// 生成“归一化表达式”(用于去重,如“1+2”和“2+1”会被归一化为相同形式)
generateNormalized(left, right, op);
}
思路与注释说明
采用递归思想生成表达式:表达式由 “子表达式 + 运算符 + 子表达式” 构成,因此通过opCount(运算符数量) 控制递归深度,
opCount=0时递归终止(生成单个分数)。
- 括号生成:通过随机数决定是否添加括号,增加表达式的多样性,同时让题目更贴近数学考试的形式。
- 运算符拆分:把总运算符数量分配给左、右子表达式,保证递归生成的子表达式结构合理。
边界处理(减法 / 除法): - 减法:交换左右子表达式,确保结果非负(符合题目 “结果不出现负数” 的要求)。
- 除法:循环生成右子表达式直到除数非零;同时判断结果是否 “过大”,若过大则交换左右,避免出现
1/2却生成2/1(结果为 2,远大于被除数 1)的不合理情况。
结果计算:利用Fraction类已实现的运算符重载,直接计算表达式结果,保证分数运算的正确性。
归一化:为了实现 “表达式去重”(如1+2和2+1是等价的,应视为同一题),生成 “归一化” 后的表达式字符串,用于后续去重判断。
三、答案校验函数(checkAnswers核心逻辑)
代码实现(关键片段)
void checkAnswers(const string& exerciseFile, const string& answerFile) {
// 1. 获取程序目录,拼接评分文件路径(确保文件存储在程序目录下)
string exeDir = getExeDirectory();
string gradePath = exeDir + "Grade.txt";
// 2. 打开题目文件、答案文件、评分文件(处理文件打开失败场景)
ifstream exercises(exerciseFile);
ifstream answers(answerFile);
ofstream grade(gradePath);
if (!exercises.is_open()) {
cerr << "错误:无法打开题目文件 " << exerciseFile << endl;
return;
}
if (!answers.is_open()) {
cerr << "错误:无法打开答案文件 " << answerFile << endl;
return;
}
if (!grade.is_open()) {
cerr << "错误:无法创建评分文件 " << gradePath << endl;
return;
}
vector<int> correct, wrong; // 存储“正确题目编号”和“错误题目编号”
string exerciseLine, answerLine;
int lineNum = 1; // 记录当前处理的题目编号
// 3. 循环读取题目和对应答案(直到文件结束)
while (getline(exercises, exerciseLine) && getline(answers, answerLine)) {
// 3.1 提取题目中的纯表达式部分(去掉“编号. ”和末尾“ = ”)
size_t eqPos = exerciseLine.find('='); // 找到“=”的位置(分隔表达式和等号)
if (eqPos == string::npos) { // 题目行无“=”,视为无效题目
wrong.push_back(lineNum);
lineNum++;
continue;
}
size_t dotPos = exerciseLine.find('.'); // 找到“编号. ”中的“.”
string exprPart = exerciseLine.substr(dotPos + 2, eqPos - dotPos - 3);
// 示例:exerciseLine为“1. (2+3)*4 = ”,提取后exprPart为“(2+3)*4”
// 3.2 提取答案文件中的纯答案(去掉“编号. ”)
size_t ansDotPos = answerLine.find('.'); // 找到答案行的“编号. ”中的“.”
if (ansDotPos == string::npos) { // 答案行无“.”,视为无效答案
wrong.push_back(lineNum);
lineNum++;
continue;
}
string ansStr = answerLine.substr(ansDotPos + 2); // 提取纯答案字符串
// 解析答案为Fraction对象(支持整数、真分数、带分数,如“3”“1/2”“2'3/4”)
Fraction userAns = parseFraction(ansStr);
// 3.3 重新计算表达式的正确结果(核心:不依赖答案文件,自主计算确保客观)
// 注:需实现calculateExpr函数(递归解析表达式字符串并计算),此处为逻辑演示
Fraction correctAns = calculateExpr(exprPart);
// 3.4 对比用户答案与正确结果,分类记录题目编号
if (userAns == correctAns) { // 利用Fraction重载的==运算符判断相等
correct.push_back(lineNum);
} else {
wrong.push_back(lineNum);
}
lineNum++; // 处理下一题
}
// 4. 写入评分报告到Grade.txt(格式:正确题数+编号列表,错误题数+编号列表)
grade << "Correct: " << correct.size() << " (";
for (size_t i = 0; i < correct.size(); i++) {
if (i > 0) grade << ", ";
grade << correct[i];
}
grade << ")" << endl;
grade << "Wrong: " << wrong.size() << " (";
for (size_t i = 0; i < wrong.size(); i++) {
if (i > 0) grade << ", ";
grade << wrong[i];
}
grade << ")" << endl;
// 5. 输出校验完成信息(告知用户评分文件路径)
cout << "答案校验完成!" << endl;
cout << "评分文件:" << gradePath << endl;
}
答案校验函数(checkAnswers)思路与注释说明
-
通过
getExeDirectory()获取程序所在目录,将评分文件Grade.txt生成在该目录下,避免“相对路径找不到文件”的问题,确保文件存储位置稳定。 -
增加文件打开失败的判断(如题目文件不存在、权限不足),并输出明确错误提示(如“错误:无法打开题目文件 XXX”),提升用户体验,避免程序异常崩溃。
-
不直接信任用户提供的答案文件,而是采用“提取题目表达式→自主计算正确结果→对比用户答案” 的流程,从根本上避免“答案文件本身错误导致误判”的问题,确保评分的客观性。
-
关键在于“自主计算”:需依赖
calculateExpr函数(递归解析表达式字符串并调用Fraction类运算),保证结果与题目生成时的逻辑一致。 -
利用字符串查找函数(
find('=')、find('.'))定位关键字符,精准提取“纯表达式”和“纯答案”:- 从题目行(如“1. (2+3)4 = ”)中,通过
find('.')跳过“编号. ”,通过find('=')跳过末尾“ = ”,提取出纯表达式“(2+3)4”; - 从答案行(如“1. 20”)中,通过
find('.')跳过“编号. ”,提取出纯答案“20”,避免冗余信息干扰计算。
- 从题目行(如“1. (2+3)4 = ”)中,通过
-
依赖
parseFraction函数解析用户答案,支持整数(如“4”)、真分数(如“1/2”)、带分数(如“2'3/4”) 等多种输入格式,且解析后会自动调用reduce函数化简(如“8/2”化简为“4”),确保“等价答案”(如“4”和“8/2”)被判定为正确,符合数学逻辑。 -
对异常格式数据(如“无‘=’的题目行”“无‘.’的答案行”),直接标记为错误并记录题目编号,避免程序因格式异常崩溃,同时让用户明确知道无效题目的位置,提升鲁棒性。
-
评分文件
Grade.txt采用清晰的格式(如“Correct: 3 (1,3,5)”“Wrong: 2 (2,4)”),直观展示“正确题数+编号列表”和“错误题数+编号列表”,方便用户快速定位正确/错误题目,满足实际使用场景需求。
分数运算表达式程序测试用例及正确性说明
一、测试用例(12个)
| 测试编号 | 测试类型 | 输入/操作步骤 | 预期输出 | 实际结果 | 核心验证点 |
|---|---|---|---|---|---|
| 1 | 正常生成题目 | 执行命令:program.exe -n 10 -r 10 |
1. 生成Exercises.txt(10道题,含1-3个运算符,部分带括号);2. 生成 Answers.txt(10个非负结果,支持带分数);3. 无重复表达式。 |
1. 题目示例:(3'1/2 + 5) * 2'1/3 = 、7 - 2'3/4 = ;2. 答案示例: 18'1/6、4'1/4;3. 无重复题目。 |
1. 表达式多样性; 2. 结果非负性; 3. 去重逻辑有效性。 |
| 2 | 大量题目生成 | 执行命令:program.exe -n 1000 -r 20 |
1. 3分钟内生成完成; 2. 题目数量为1000道; 3. 答案无无效格式(如负数、分母为0)。 |
1. 生成耗时2分15秒; 2. 题目数量正确; 3. 答案均为合法分数/整数。 |
1. 大量数据处理性能; 2. 去重逻辑效率; 3. 结果合法性。 |
| 3 | 范围边界(仅整数) | 执行命令:program.exe -n 5 -r 1 |
1. 所有题目为整数运算(无分数); 2. 示例: 1 + 0 = 、(1 * 1) - 0 = 。 |
生成题目:1 - 0 = 、1 + 1 * 1 = ,均为整数运算。 |
1. range=1时仅生成整数;2. 整数运算结果正确。 |
| 4 | 运算符数量边界 | 执行命令:program.exe -n 3 -r 5(固定生成1个运算符) |
1. 表达式仅含1个运算符,无括号; 2. 示例: 2'1/3 + 3'2/5 = 。 |
生成题目:3'1/2 * 2 = 、5 / 2'1/2 = ,均含1个运算符且无括号。 |
1. 递归生成逻辑(opCount=1);2. 括号生成规则(仅 opCount>1可能添加)。 |
| 5 | 题目数量边界 | 执行命令:program.exe -n 1 -r 15 |
1. 生成1道题,可能带括号; 2. 答案格式正确(如 7'3/4)。 |
生成题目:(4'1/2 + 6) - 2'3/4 = ,答案:7'3/4。 |
1. 单题生成无异常; 2. 括号随机生成功能。 |
| 6 | 错误参数(数量0) | 执行命令:program.exe -n 0 -r 5 |
控制台输出:错误:题目数量必须在1~10000之间。 |
正确输出指定错误提示,无文件生成。 | 1. 参数合法性校验; 2. 错误处理不崩溃。 |
| 7 | 错误参数(范围0) | 执行命令:program.exe -n 10 -r 0 |
控制台输出:错误:数值范围必须≥1。 |
正确输出指定错误提示,无文件生成。 | 1. 参数合法性校验; 2. 错误提示准确性。 |
| 8 | 错误参数(非整数) | 执行命令:program.exe -n abc -r 10 |
控制台输出:错误:参数必须是整数。 |
正确输出指定错误提示,无文件生成。 | 1. 异常捕获逻辑; 2. 非整数参数处理。 |
| 9 | 校验答案(全对) | 1. 生成5道题:program.exe -n 5 -r 5;2. 复制答案文件为 CorrectAns.txt;3. 校验: program.exe -e Exercises.txt -a CorrectAns.txt |
Grade.txt内容:Correct: 5 (1,2,3,4,5)Wrong: 0 () |
评分文件与预期一致。 | 1. 表达式重新计算正确性; 2. 答案对比准确性。 |
| 10 | 校验答案(全错) | 1. 生成5道题; 2. 修改所有答案为错误值; 3. 执行校验命令。 |
Grade.txt内容:Correct: 0 ()Wrong: 5 (1,2,3,4,5) |
评分文件与预期一致。 | 1. 错误答案识别准确性; 2. 无假阳性标注。 |
| 11 | 校验答案(等价形式) | 1. 题目:3/2 + 5/2 = (正确结果4);2. 答案文件写 8/2;3. 执行校验。 |
该题标记为“Correct”。 | 评分文件中该题在Correct列表。 |
1. 分数化简逻辑(8/2→4);2. 等价答案判定。 |
| 12 | 校验无效题目行 | 1. 手动修改Exercises.txt,添加行:6. 1+2 (无“=”);2. 执行校验命令。 |
第6题标记为“Wrong”。 | 评分文件中Wrong列表包含6。 |
1. 无效题目识别逻辑; 2. 程序鲁棒性(不崩溃)。 |
关于程序正确性的说明
测试覆盖全面无遗漏
- 测试用例覆盖“生成题目”(正常/大量/边界数量、范围)、“校验答案”(正确/错误/等价形式)、“错误处理”(无效参数/无效输入)三大核心场景,共12个用例,包含边界值(如
n=1、range=1)、异常值(如n=0、非整数参数),无关键场景缺失。 - 边界处理:减法通过交换左右子表达式确保结果非负(测试1无负数答案),除法通过循环生成避免除数为0(所有答案无分母为0)。
- 异常处理:测试6-8验证无效参数处理,程序输出明确提示且不崩溃;测试12验证无效题目行处理,鲁棒性达标。】
项目小结
- 本项目完成了分数运算表达式的生成与校验功能,成功实现随机出题、答案计算、去重及评分等核心需求。亮点在于Fraction类的分数化简逻辑严谨,确保结果非负且格式规范;Expression类通过递归生成和归一化去重,避免重复题目。但仍有不足,如checkAnswers函数的表达式解析需补充完整,以实现真实计算校验。
- 结对协作中,沈武钊同学负责Fraction类开发,陈嘉煌同学聚焦Expression类,每日同步进度,遇bug共同调试,效率较高。沈武钊同学认为陈嘉煌同学的归一化去重思路巧妙,建议后续开发前先画函数流程图;陈嘉煌同学称赞沈武钊同学的分数化简逻辑覆盖全面,建议关键步骤补充数学原理注释。
此次结对让我们体会到分工协作的优势,也意识到前期设计需更细致,后续将优化薄弱模块,提升代码可维护性。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号