高级搜索树

• 伸展树

1. 通过 Splay/伸展操作 不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，能够在均摊 O(logn)时间内完成插入，查找和删除操作
2. 局部性。如刚刚被访问的节点，极有可能很快的再次被访问，下一次要访问的节点，极有可能就在刚被访问的节点附近。
3. 伸展树是局部性原理的应用：将刚被访问的节点，随即通过zag zig旋转操作被转移至树根。调整的过程逐层摇摆，逐渐上升--伸展树。“一步一步往上爬”。
4. 伸展树存在最坏情况。当伸展树退化成类似链表的结构时，旋转次数每一周期累计omiga(n^2) ，分摊下来omiga(n)。
5. 双层伸展--“点睛之笔”，一次性上升两层。在子孙异侧的情况下，伸展两层就是伸展两次（与单层伸展没有不同）；但是在子孙同侧的情况下，调整的时候从祖父开始而不是父节点，这会使局部的拓扑结构产生微妙的差异，这种微妙的差异将会带来全局的不同。
6. 双层伸展，具有折叠的效果，一旦访问最坏节点，对应路径长度减半，最坏情况不致持续发生，分摊性能单趟不超过O(logn)。
7. 对于伸展树而言，查找动作不再是一个静态操作，这是一个本质特征。插入删除实现可以很简单，因为在插入删除之前一定做过一次查找操作，一定会将该节点或相邻节点移至树根O（logn）。
8. 综合评价：优点：无需记录节点高度或者平衡因子：编程简单易行--优于AVL树。分摊复杂度O(logn)与--AVL树相当。局部性强缓存命中率极高。缺点：仍不能保证单次最坏情况的出现，不适用于单次操作对效率敏感的场合。

• B-树（多路平衡搜索树）

1. 越来越大的数据，内存容量相对越来越小。不同容量的存储器，访问速度差异悬殊。若一次内存访问需要一秒，则一次外存访问需要一天。所以采用了多级cache，分级I/O。另外一个事实：从磁盘上读写一B，与读写1kB几乎一样快。
2. B树的节点 可以看成二叉树 每两代或多代合并后的超级节点。一般所谓m阶B树，即m路平衡搜索树（m>=2）。
3. 多级存储系统中使用B-树，可针对外部查找，大大减少I/O次数。比如有1G个记录用平衡树大约30层，每一层进行一次I/O访问，需要三十层I/O访问。而对于B树，若一个超级节点当中的关键码有256个，同样1G个记录只有4层树高。
4. m阶B树 给出了B树中每个超级节点的上限和每个超级节点的下限。在上限方面，每个节点的分支数都不能超过m个，在下限方面，每个节点的分支数也不能太少，不能少于m的一半的上整。对于树根来说分支数 >=2 即可。用分支数的下限上限来命名B树，【m/2取上整，m】阶B树。
5. B树的查找：一系列的顺序查找+I/O操作（内存+外存操作）。B树的高度上下浮动有限。复杂度：渐进意义下O(logn)，但是B树的优化关注于常系数意义下的优化，因其可以减少I/O次数。
6. B树的插入 O(h)。若分裂，上溢：设上溢出的节点中的关键码依次为k0, ......., kn-1，取中位数，s=m/2取上整，以关键码为界ks划分为k0,...ks-1,ks,ks+1,....kn-1，关键码上升一层，并分裂以所得的两个节点作为左右孩子。上溢缺陷可能会传播，但是只会逐层向上，最坏情况，不过到根。插入操作可能导致B树增高。
7. B树的删除 O(h)。 下溢，合并。

• B+树

1. B+树是B树的变种
2. 所有的非叶子节点可以看成是索引部分
3. 所有叶子节点中包含了全部关键字的信息，及指向含这些关键字记录的指针
4. B+ 树为了方便范围查询，叶子节点之间还用指针串联起来
5. 由于索引节点上只有索引而没有数据，所以索引节点上能存储比 B 树更多的索引，这样树的高度就会更矮。树的高度越矮，磁盘寻道的次数就会越少。
6. 因为数据都集中在叶子节点，而所有叶子节点的高度相同，那么可以在叶子节点中增加前后指针，指向同一个父节点的相邻兄弟节点，这样可以更好地支持查询一个值的前驱或后继，使连续访问更容易实现。

• 红黑树

1. 无论是线性结构如向量，半线性结构树，非线形结构图，每经过一次动态操作后，逻辑结构有所改变，随即完全转入新的状态，将之前的状态完全遗忘掉，为非持久性结构。在实际情况中，我们可能很看重持久性
2. 红黑树：任何一次动态操作引发的结构变化量不致超过O(1)。持久性。
3. 红黑树模型：树根必为黑色；外部节点均为黑色；其余节点，若为红，则只能有黑孩子；外部节点到根，途中黑节点数目相同。
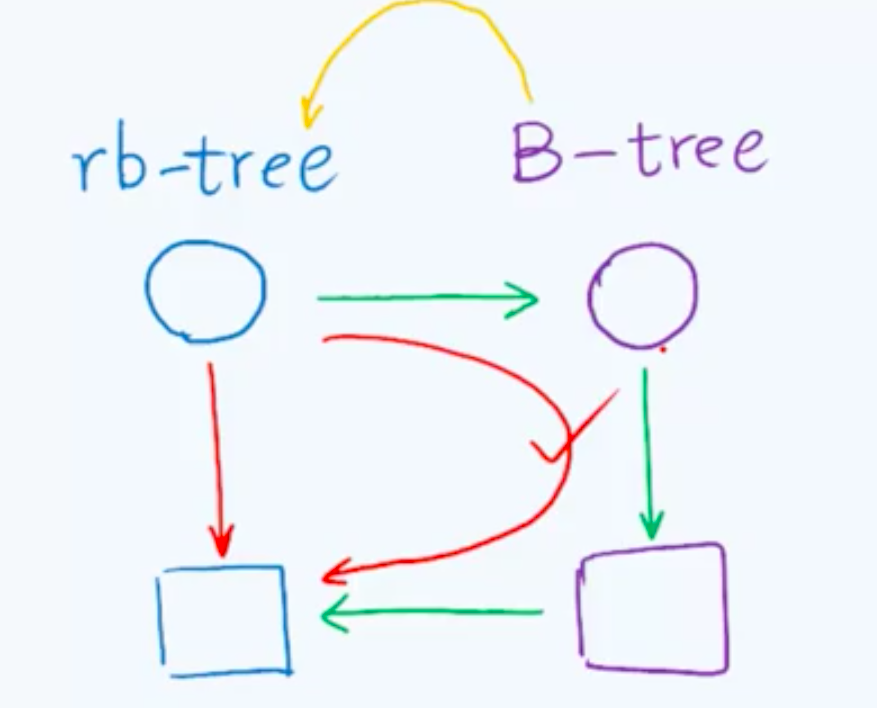
4. 红黑树经过提升变换后，红孩子与黑父亲平齐。等同视为一个（2，4）B树。红黑树 == （2，4）树。红黑树具有平衡性。
5. 红黑树插入 我们不妨将插入的节点染红，如果该节点的父节点是黑色，则插入成功，如果该节点的父亲节点是红色，则产生双红缺陷。双红缺陷的其一情况解决，只需要交换相邻节点颜色即可，然后进行局部“3+4”重构。拓扑结构变换O(1)。双红缺陷的其二情况解决，从B树的角度来看是修复上溢的过程，对应到红黑树只是做了染色操作，双红缺陷可能向上传播，不过最多到根，尽管染色操作可能到O(logn)，拓扑结构的变化仍为O(1)。整个的修复过程中最多执行O(logn)的染色操作，最多执行一次重构操作。
6. 红黑树删除O(logn)  删除某一节点，被某后代节点替代。被删节点和替代者之间有一个为红，只需将替代者染黑即可。被删节点和替代者都为黑，双黑缺陷。修复双黑缺陷，从B树的角度来看则是修复下溢缺陷。修复缺陷最多做O(logn)次重染色，一次“3+4”重构，一次单旋。
7. 红黑树的插入删除都在O(logn)以内完成，红黑树具有持久性。