基环树

基环树，顾名思义，就是基于环的树。

简单的来说就是环上每个结点都以它自己为根建一棵树，或者在一棵树上多加一条边。

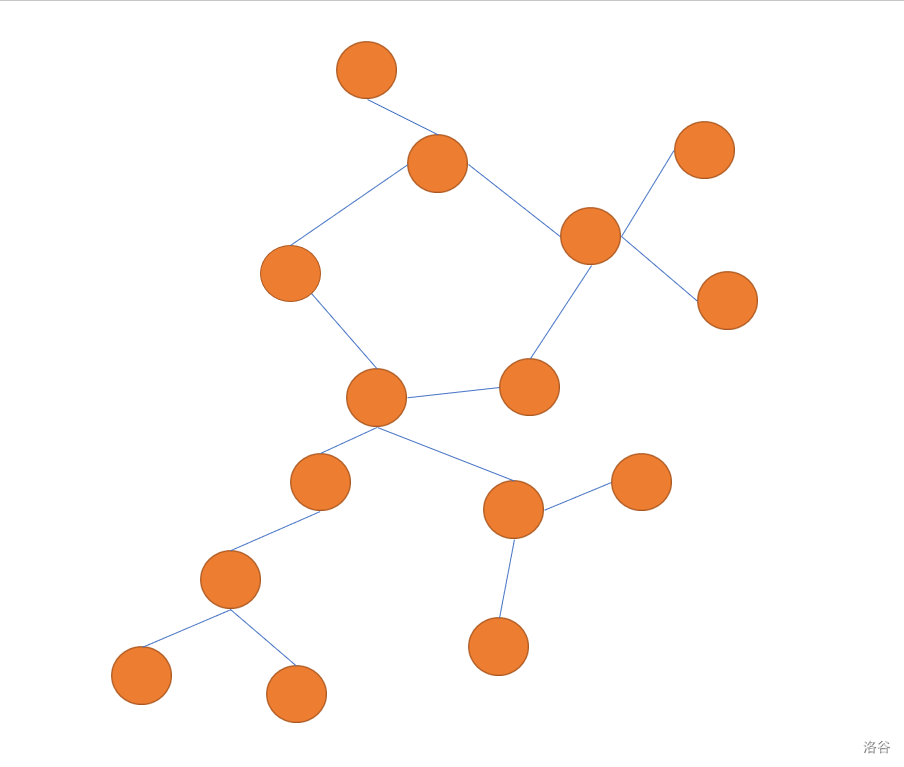
如上图所示，这就是一颗基环树。（可能有点丑陋）

所以你会发现基环树有一些优美的性质。

• 1.基环树的点数等于边数且连通

• 2.在基环树的环上任意断一条边，所得的图一定是一棵树

显然，基环树比树略微复杂。

基环树森林

树的森林大家都知道吧，就是有很多棵树的图。简单的来说就是图不连通，但没有环。

那么什么是基环树森林呢？以上面为例就知道是很多基环树的图了。那么基环树森林有什么特点呢？

• 基环树森林的点数等于边数

这个很容易证明。因为这个图的每一个连通图都是基环树，所以每一个连通图的点数都等于边数，合起来就是总点数等于总边数了。

那么，如果已知一个图中点数等于边数，那么它一定就是基环树森林吗？

不对！我们可以构造两个连通图，一个图是一棵树，一个图是树加两条边。显然总点数仍然等于总边数，但是两个图都不是基环树。（下次就不要掉进坑里了）

造数据

如果你出过关于基环树的题，那么你一定需要用随机数据构造基环树或者基环树森林。

我们可以用一个 \(\text{struct}\) 数组来存一条边连接着两个端点。根据基环树的定义可以知道，可以先随机环，再随机边。于是我们先随机环的长度，随机环上的点，一个环就随机完了。随机边的时候，要注意此时一条边已经用在环上了，所以随机的两个点都不能在一个连通块才能使总边数等于总点数。我们可以使用并查集来维护。

如果有人问：怎么判断自环或重边？我只能告诉你并查集太好用了，一次性解决所有问题。上面两种情况实际上都是两个端点在一个连通块，可以直接舍掉。至于环我们将环的长度的下界设为 \(3\)，就能避免环长为 \(2\) 时出现重边，环长为 \(1\) 时出现自环的情况。

#include <iostream>
#include <ctime>
#include <cstdlib>
#include <algorithm>
using namespace std;
int f[200005],n,lenhuan,inc[500005],b[500005],cnt;
struct node
{
	int e,f;
}eg[200005];
int Rand(int x)//随机0~x-1之间的数
{
	return (rand() % 10 * 100000000 + rand() % 10000 * 10000 + rand() % 10000) % x;
}
int find(int x)//并查集
{
	if(f[x] == x)return x;
	return f[x] = find(f[x]);
}
int main()
{
	srand(time(0));
	n = 10;
	lenhuan = Rand(n - 2) + 3;//取值范围为3~n
	for(int i = 1;i <= n;i ++)f[i] = i;
	for(int i = 1;i <= lenhuan;i ++)
	{
		int x = Rand(n) + 1;
		while(inc[x])x = Rand(n) + 1;//inc[x]:判断是否已经在环内
		inc[x] = 1,b[++cnt] = x;
	}
	eg[1].e = b[1],eg[lenhuan].f = b[1];
	for(int i = 1;i < lenhuan;i ++)f[b[i]] = b[i + 1];
//环上的点属于一个连通块
	for(int i = 1;i < lenhuan;i ++)eg[i].f = eg[i + 1].e = b[i + 1];//存储环上的点
	for(int i = lenhuan + 1;i <= n;i ++)
	{
		int x = Rand(n) + 1,y = Rand(n) + 1;
		while(find(x) == find(y))x = Rand(n) + 1,y = Rand(n) + 1;
//连接两个不同连通块
		eg[i].e = x,eg[i].f = y,f[find(x)] = find(y);
	}
	for(int i = 1;i <= n;i ++)
	{
		if(rand() % 2)swap(eg[i].e,eg[i].f);//增加随机性
		cout << eg[i].e << " " << eg[i].f << '\n';
	}
}

注意：上面那份代码的边没有打乱顺序，请使用 \(\text{random\_shuffle}\) 打乱。简单的来说， \(\text{random\_shuffle(a + 1,a + n + 1)}\) 可以将 \(a_1\sim a_n\) 重新排列，大家可以试一下。

基环树dp

做基环树的题的主要思想是：断环为链，也可以称作：断基环树为树。

直接上例题吧。

P1453 城市环路

\(n\) 点 \(n\) 边且连通可以锁定图是基环树。那么怎么 dp 呢？

我们发现，对于环上两个相邻的点，它们两个最多选一个。我们可以将那条边断掉，分别对第一个点一定不选和第二个点一定不选分别求结果，这样就能覆盖所有的可能性。答案取 \(\max\) 即可。结合图片可能能更好理解。

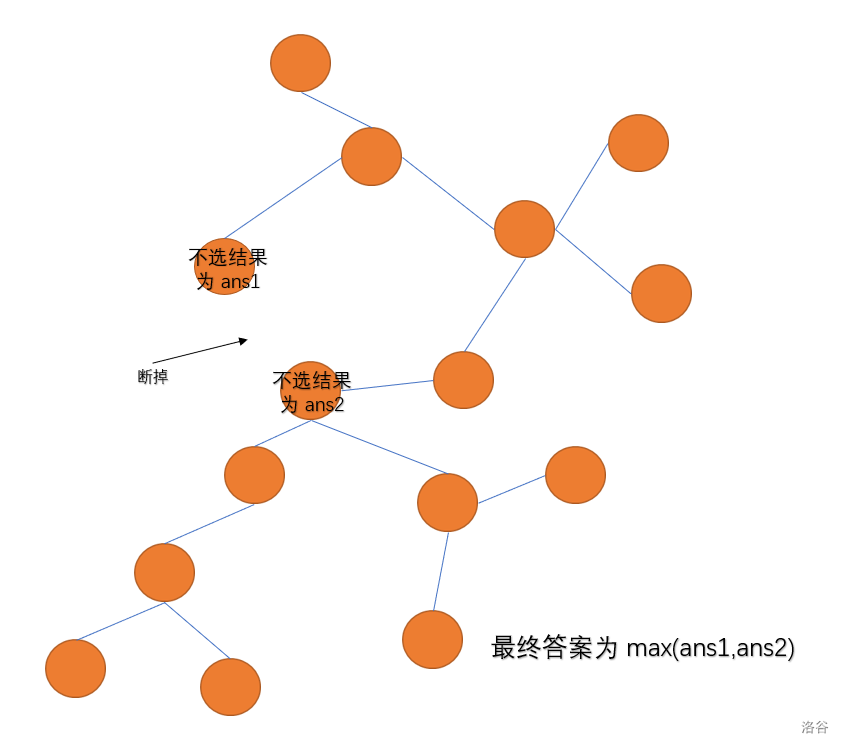
然后图就转换成了一棵树。后面基本上就对标 没有上司的舞会了，我们设断开的边连接着的两个端点为 \(ux,uy\) ，分别以 \(ux\) 和 \(uy\) 跑一遍树形 dp。我们可以设状态 \(dp_{i,0/1}\) 表示以结点 \(i\) 选（1）或不选（0）的最大利润（只算一个点的祖先有点 \(i\) 的情况），那么根据题目要求 \(dp_{u,1} = \sum dp_{v,0}\) （\(u\) 为 \(v\) 的父亲），因为选点不能相邻；而 \(dp_{u,0} = \sum \max(dp_{v,0},dp_{v,1})\)。先求儿子，再求父亲，答案就为根节点不选时的答案。

最后一个问题：我们如何确定断的是环上的边呢？很简单。用并查集来维护，如果一条边连接着的两个端点属于同一个连通块，则必然构成环边。不妨试着画图理解一下。

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
vector<int>ve[100006];
int n,a[100005],gen,b[100005],dp[100005][3],c[100005],f[100005],ux,uy;
double k;
int dfs(int x,int num,int fa)//求dp[x][num]的最大利润，祖先是fa
{
	if(dp[x][num])return dp[x][num];//重复调用直接返回（当然这道题不需要
	int ans = 0;
	if(num)ans += a[x];//如果选加上该贡献
	for(int i = 0;i < ve[x].size();i ++)
	{
		if(ve[x][i] == fa)continue ;
		if(num == 0)ans += max(dfs(ve[x][i],0,x),dfs(ve[x][i],1,x));//不选取max
		else ans += dfs(ve[x][i],0,x);//选儿子只能都不选
	}
	return dp[x][num] = ans;//返回结果并记录答案
} 
int find(int x)
{
	if(f[x] == x)return x;
	return f[x] = find(f[x]);
}
int main()
{
    cin >> n;
    for(int i = 0;i < n;i ++)cin >> a[i],f[i] = i;
    for(int i = 1;i <= n;i ++)
    {
        int x,y;
        cin >> x >> y;
        int w = find(x),w2 = find(y);
        if(w != w2)ve[y].push_back(x),ve[x].push_back(y),f[w] = w2;
        else{
        	ux = x,uy = y;//是环边，记录，并断开
		}
    }
    cin >> k;
    int ue = dfs(ux,0,100002);//注意，因为有0号点的存在，fa不能设0，当然也可以设-1
    memset(dp,0,sizeof(dp));//记得初始化
    printf("%.1lf",k * (double)max(ue,dfs(uy,0,0)));//求最大值
}

是不是很简单？那恭喜你还获得了一个双倍经验：P2607 骑士，只不过这题是基环树森林。

你可能会说：\(n\) 条边 \(n\) 个点不是不一定是基环树森林吗？

这是个例外！因为一个人只有一个最讨厌的战士，而环已经满足所有人都有最讨厌的战士了（环里面有树也一样，因为树的部分他们只能向环内讨厌），再加一条边总会出现有人有两个最讨厌的战士。所以这种输入可以满足所给的图是一个基环树森林，这也是构造基环树森林的一种常见方法。（甚至比构造基环树还要简单）

基环树找环

我们再来看一道题：

P5022 旅行

注意数据范围，\(\mathcal{O(n^2)}\) 能过。

所以一个很暴力的思路就出来了：暴力把环边断掉，然后以 \(1\) 为根往下走它儿子中最小的那个就行了（贪心思想）。

void dfs(int x,int fat)//fat是fa，因为后面有fa数组，导致重名改了一下
{
	cout << x << " ";
	for(int i = 0;i < ve[x].size();i ++)
		if(ve[x][i] != fat)dfs(ve[x][i],x);
}
for(int i = 1;i <= n;i ++)sort(ve[i].begin(),ve[i].end());
//这是主函数内的一句话，保证访问的儿子是从小至大的

那么我们现在的首要目的是找出所有的环边（上面的例题只要求找一处）。

tarjan 算法可以实现这个目的（没学过的敬请收看同学的博客）。

我们可以从 \(1\) 开始依次遍历基环树，正常来说（树）当一个结点不是自己的父亲时是肯定没有访问过的，那么既不是父亲又已经访问就说明出现环了（见下图）

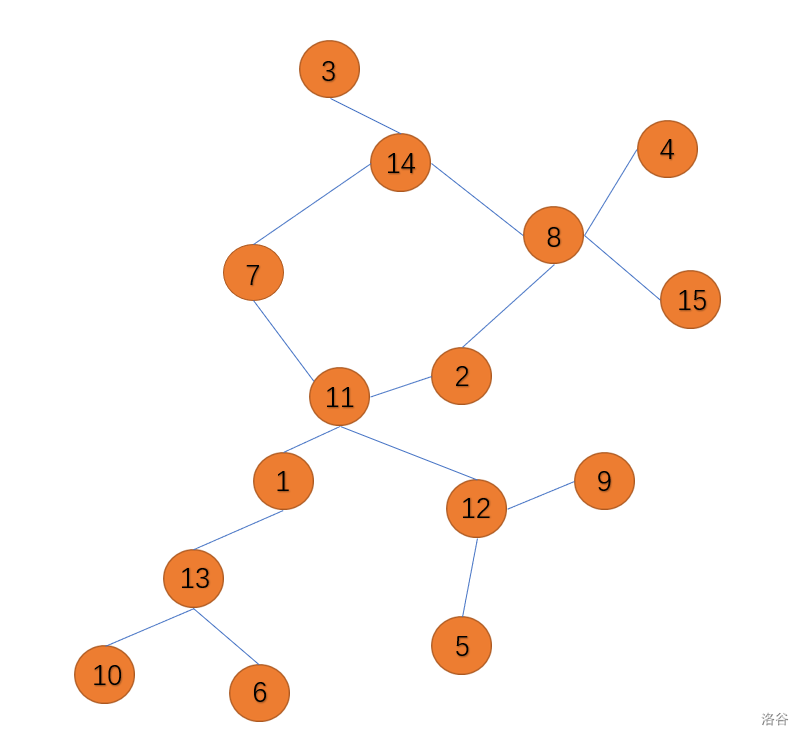
我们一边记录访问一边记录父亲。假设访问的顺序是这样的：\(1\to13\to10\to6\to11\to2\to8\to4\to14\to3\to7\)

那么下一个就要访问 \(11\) 了。但是 \(11\) 已经访问过，就说明构成环了。所以这就是这两个结点夹着的就是环边。

慢着！那不还是只找了一个环边吗？

这就是为什么要记录父亲。我们顺着 \(7\) 的父亲一直往回走： \(7\to14\to8\to2\to11\)。当走到 \(11\) 时，环上的结点就全部找到了。在记录环上的点时，可以顺带记一个点 \(x\) 在不在环内。

我们用 \(\text{bool}\) 类型的函数来完成递归。当后面找到环时，可以返回 \(1\) 及时退出函数。

bool find_huan(int x)
{
	vis[x] = 1;//访问数组
	for(int i = 0;i < ve[x].size();i ++)
		if(ve[x][i] != fa[x])//若连接着的是自己的儿子
		{
			fa[ve[x][i]] = x;
			if(!vis[ve[x][i]])//没访问，继续查找
			{
				if(find_huan(ve[x][i]))return 1;
			}
			else
			{//出现环
				int p = x;
				while(1)//沿着父亲跳
				{
					wv[++all] = x,in[x] = 1;
					x = fa[x];
					if(p == x)break ;
				}
				return 1;
			}
		}
	return 0;//没找到环
}

找到环边后，这道题基本上就做出来了。

当然，基环树还远不止这一些，还有基环树的直径等内容。但是这篇博客只讲基础，弄懂基环树的原理就行。