线段树详解
顾名思义,线段树是一种树,而且树的每一个结点是一条线段而不是结点编号。这是线段树的形态:
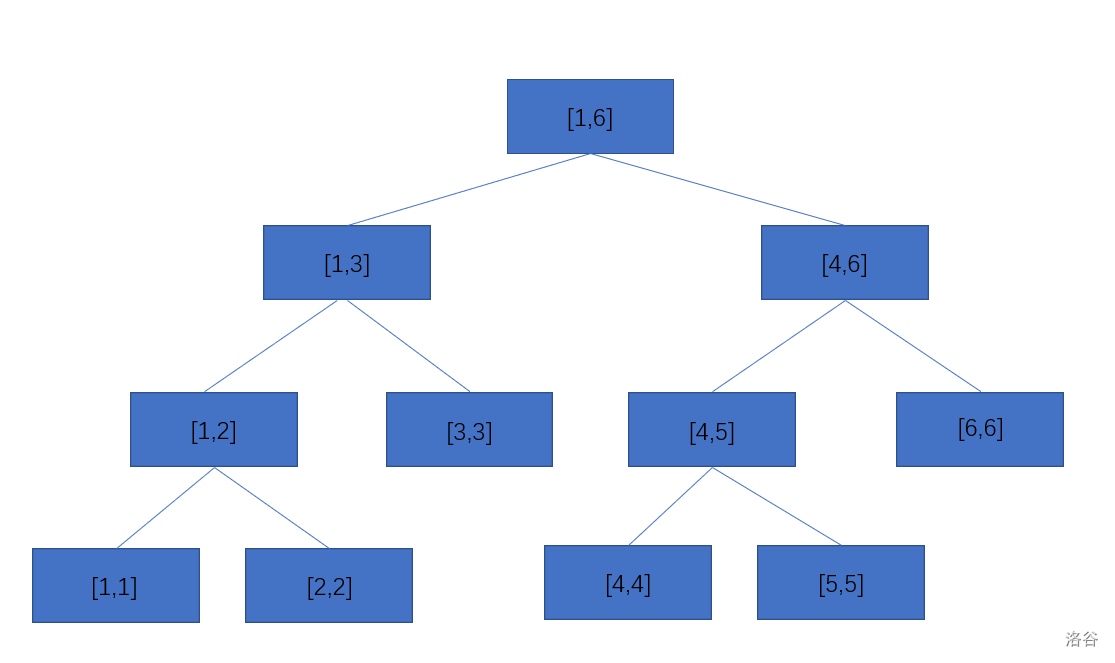
简单的来说,树的根(最上面那个节点)是我们需要维护的大区间,然后以该区间的中间值 \(mid\) 分为两个儿子 \(l,mid\) 和 \(mid + 1,r\),然后又一层一层的分裂,直到 \(l = r\) 为止。为了表示方便,我们默认将根节点的下标存储在 \(0\) 号位置(\(1\) 号也行),那么,编号为 \(x\) 的两个儿子的编号即为 \(x \times 2 + 1\) 和 \(x \times 2 + 2\)。我们会发现,\(0\) 的两个儿子的编号是 \(1,2\),\(1\) 的两个儿子的编号是 \(3,4\) ...... 这样我们就不重不漏的使用所有空间来构建这颗线段树。
具体代码。
struct tree //线段树
{
int ze,ye;//结点的两个儿子
}tr[2000005];//下标
void build(int x,int l,int r)
{//建立线段树的函数,其中 x 表示当前构建结点的编号,l和r表示该节点包含的区间
tr[x].ze = l;
tr[x].ye = r;//记录
if(l == r)return ;//最底层,直接返回
int mid = (l + r) / 2;//求区间的mid
build(x * 2 + 1,l,mid);
build(x * 2 + 2,mid + 1,r);
//分裂成两条线段,其中该线段左儿子区间的右端点是mid,右儿子区间的左端点是mid + 1
//两个儿子的编号分别为 x * 2 + 1 和 x * 2 + 2
}
可以结合代码和文字理解。
当我们想要构建线段树时,只需要在主函数写一句 build(0,1,n) 就行了。(其中 \(n\) 表示你想构建的线段树的长度)
于是我们就得到了图示所给的线段树。(\(n = 6\),其中红色数字为该节点的下标)
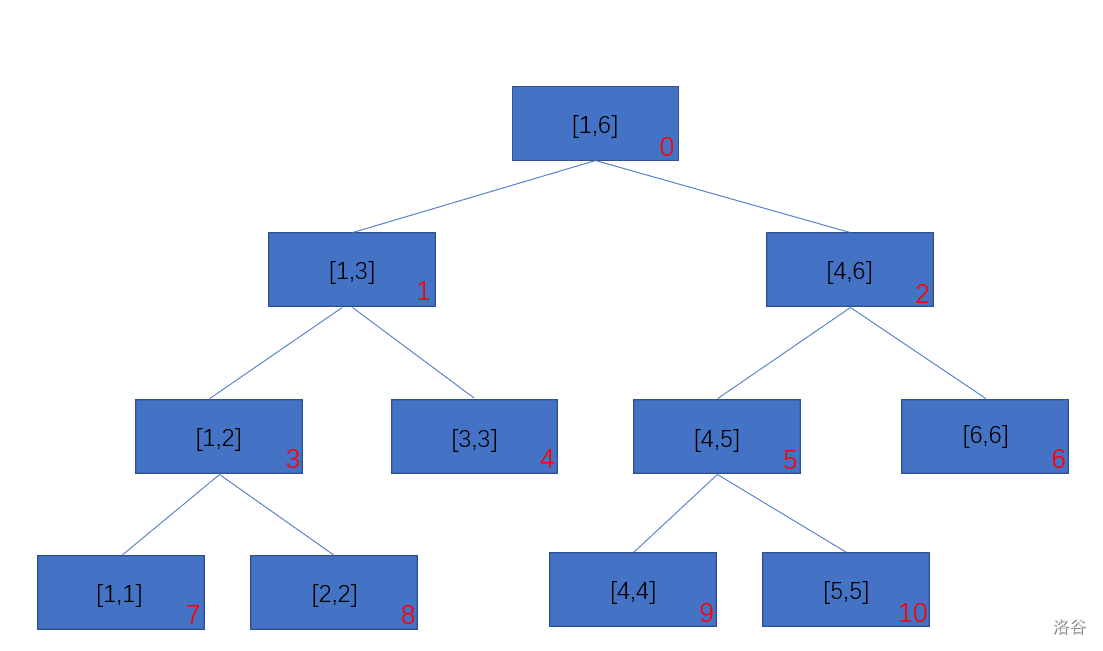
那么,我们要这颗线段树有什么用呢?
我们不妨来看一看线段树的模板题。
在一般情况下,区间加和区间求和的复杂度都是 \(\mathcal{O(n)}\) 的。那么有没有一种更快速的方法解决这么一道题目呢?我们就用到了线段树。
很显然,线段树需要维护一个东西,那就是区间和。这是我们所要求的。
那么,一条线段 \([l,r]\) 可以怎么求出它的区间和呢?
我们可以把它分成 \(\log n\) 条小的线段,这些线段的并就是 \([l,r]\),而这些小线段的和就等于线段 \([l,r]\) 的和。
所以问题就很明了了:我们只需要利用上面那颗线段树,将所有小区间的和都求出来,询问时就利用上面那个方法求和就行了。为了维护小区间的和,结构体 \(\text{tree}\) 中需要多开一个数 —— \(sum\),表示该结点包含的区间内所有数的和。
这题首先需要输入 \(n\) 个数 \(a_i\)。因为这种输入在查询与修改之前,所以我们也应该在修改之前——也就是 \(\text{build}\) 函数中处理好它。
首先我们想一想当 \(l = r\) 的时候区间的和。这不用提就是 \(a_l\) 的值了。那么接下来,当 \(l = r - 1\) 的时候呢?
从上面那幅图来看,它的下面有两个儿子,而两个儿子包含区间的长度都是 \(\dfrac{2}{2} = 1\)。我们可以先把两个儿子的 \(sum\) 求出来,那么这两个 \(sum\) 相加就是这个儿子的 \(sum\) 了。
依次类推,我们发现,先求出结点 \(x\) 两个儿子的 \(sum\),它们两个相加就是结点 \(x\) 的 \(sum\) 了。这样的话,我们就实现在建树(\(\text{build}\))阶段就求出所有小线段的和了。
struct tree
{
int ze,ye,sum;//sum维护该结点的和
}tr[2000005];
void build(int x,int l,int r)
{
tr[x].ze = l;
tr[x].ye = r;
if(l == r)//l=r时区间和显然为a[l]
{
tr[x].sum = a[l];
return ;
}
int mid = (l + r) / 2;
build(x * 2 + 1,l,mid);
build(x * 2 + 2,mid + 1,r);
tr[x].sum = tr[x * 2 + 1].sum + tr[x * 2 + 2].sum;//等于它的两个儿子的sum和
}
当 \(a\) 数组为 \([7,0,5,5,2,6]\) 的时候,线段树内结点维护的和为下面一张图:
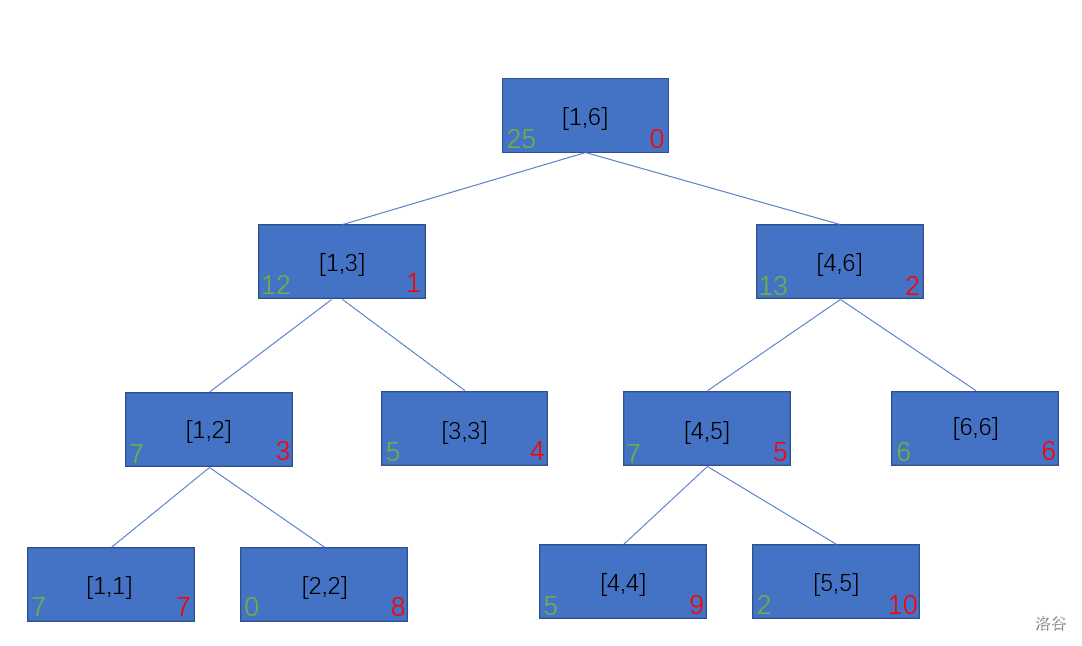
我们发现多了一个绿色,那就是该节点所维护区间的和。
由此我们就可以用 \(\text{query}\) 函数来求任意区间的和了。
比如:当查询的区间为 \([1,5]\) 时,它并不能包含 \([1,6]\),便下找它的两个儿子。\([1,3]\) 被全部包含了,答案直接加上它的结果 \(12\);\([4,6]\) 没有完全被包含,继续递归;\([4,5]\) 也被完全包含,答案加上他的结果 \(7\);\([6,6]\) 不包含,答案肯定没有该区间的值,直接返回。就这样,\([1,5]\) 被拆成了 \([1,3]\) 和 \([4,5]\),我们就能求出它的值的和等于 \(19\) 了。
int query(int x,int l,int r)
{//注意l,r不表示结点维护的区间,而是求查询区间的总和
if(l > r)return 0;//查询区间长度<=0,答案肯定为0
if(l <= tr[x].ze && tr[x].ye <= r)return tr[x].sum;
//该结点被查询区间完全包含,答案肯定有该区间的所有值
int mid = (tr[x].ze + tr[x].ye) / 2,ans = 0;//注意不是(l + r) / 2;
ans += query(x * 2 + 1,l,min(r,mid));
//左端点内区间的值,注意r要对mid取min,因为是分段考虑
ans += query(x * 2 + 2,max(l,mid + 1),r);//右端同理
return ans;//最后结果的值
}
我们想要知道 \([1,5]\) 的和直接输出 query(0,1,5) 即可。换做题目就是 query(0,l,r)。
但是,这道题并不只有区间查询的操作,还有区间加的操作。这又该怎么办呢?
有人会说:这和 \(\text{query}\) 函数不是一样的吗,都是将大块分成小块加?
那很容易发现错误:我们将大块加了之后,如果查询到的是大块之中的一个小块,那么结果就没有大块整体加的这一个结果。如上图,当我们区间加 \([1,5]\) 时,按照上面的思路,\([1,5]\) 会分成 \([1,3]\) 和 \([4,5]\) 加在两个区间块上。但是查询 \([4,4]\) 这个区间的和时,函数会返回区间 \([4,5]\) 下面的区间 \([4,4]\) 的值,导致漏算了区间加的值,从而出错。
所以我们需要一个新的变量 \(add\) 表示每个区间的懒标记(lazy_tag)。
懒标记是怎么来的?
相信突然多了一个变量很多人就会有着这种疑惑。其实,懒标记就是用来解决上面的问题的。最朴素的办法是将 \([1,3]\) 和 \([4,5]\) 下面的所有儿子全部操作区间加。但是我们发现,这样的效率太慢了,还没有暴力的效率高。但是我们并不一定每一次操作后都立马下传区间加的信息,可以等到必须要调用时才加。因此,懒标记就这么诞生了。
懒标记,顾名思义,就是“懒”,事情推迟再做。有区间加的操作时,分成很多个小区间,我们不直接下传,而是等到下次再调用时再上传。我们可以用 if(add) 判断当前结点有无懒标记。如果有,则下传避免影响结果。
好了这是此部分的代码。
void pushdown(int p)//懒标记下传
{
tr[p * 2 + 1].sum += tr[p].add * (tr[p * 2 + 1].ye - tr[p * 2 + 1].ze + 1);//下传sum
tr[p * 2 + 2].sum += tr[p].add * (tr[p * 2 + 2].ye - tr[p * 2 + 2].ze + 1);
tr[p * 2 + 1].add += tr[p].add;
tr[p * 2 + 2].add += tr[p].add;//add不要忘了下传
tr[p].add = 0;
}
void jia(int x,int l,int r,int k)//k:加的数
{
if(l > r)return ;
if(l <= tr[x].ze && tr[x].ye <= r)
{
tr[x].sum += (tr[x].ye - tr[x].ze + 1) * k;//记得乘上该区间内的长度
tr[x].add += k;//懒标记
return ;
}
pushdown(x);//如果该节点需要调用,需要将懒标记下传
int mid = (tr[x].ze + tr[x].ye) >> 1;
jia(x * 2 + 1,l,min(r,mid),k);
jia(x * 2 + 2,max(l,mid + 1),r,k);
tr[x].sum = tr[x * 2 + 1].sum + tr[x * 2 + 2].sum;//这一句不要忘,要更新父节点
}
此外,因为有了懒标记的存在,所以 \(\text{query}\) 函数也不要忘了下传。
然后我们就维护了区间加区间查询的操作。
此题就完成了。
#include <iostream>
#define int long long
using namespace std;
int a[2000005],n,m;
struct tree
{
int ze,ye,sum,add;//注意新增一个变量add
}tr[2000005];
void pushdown(int p)
{
tr[p * 2 + 1].sum += tr[p].add * (tr[p * 2 + 1].ye - tr[p * 2 + 1].ze + 1);
tr[p * 2 + 2].sum += tr[p].add * (tr[p * 2 + 2].ye - tr[p * 2 + 2].ze + 1);
tr[p * 2 + 1].add += tr[p].add;
tr[p * 2 + 2].add += tr[p].add;
tr[p].add = 0;
}
void build(int x,int l,int r)
{
tr[x].ze = l;
tr[x].ye = r;
tr[x].sum = tr[x].add = 0;
if(l == r)
{
tr[x].sum = a[l];
return ;
}
int mid = (l + r) / 2;
build(x * 2 + 1,l,mid);
build(x * 2 + 2,mid + 1,r);
tr[x].sum = tr[x * 2 + 1].sum + tr[x * 2 + 2].sum;
}
void jia(int x,int l,int r,int k)
{
if(l > r)return ;
if(l <= tr[x].ze && tr[x].ye <= r)
{
tr[x].sum += (tr[x].ye - tr[x].ze + 1) * k;
tr[x].add += k;
return ;
}
pushdown(x);
int mid = (tr[x].ze + tr[x].ye) >> 1;
jia(x * 2 + 1,l,min(r,mid),k);
jia(x * 2 + 2,max(l,mid + 1),r,k);
tr[x].sum = tr[x * 2 + 1].sum + tr[x * 2 + 2].sum;
}
int query(int x,int l,int r)
{
pushdown(x);
if(l > r)return 0;
if(l <= tr[x].ze && tr[x].ye <= r)return tr[x].sum;
int mid = (tr[x].ze + tr[x].ye) / 2,ans = 0;
ans += query(x * 2 + 1,l,min(r,mid));
ans += query(x * 2 + 2,max(l,mid + 1),r);
return ans;
}
signed main()
{
cin >> n >> m;
for(int i = 1;i <= n;i ++)cin >> a[i];
build(0,1,n);
for(int i = 1,opt,x,y,z;i <= m;i ++)
{
cin >> opt;
if(opt == 1)cin >> x >> y >> z,jia(0,x,y,z);
else cin >> x >> y,cout << query(0,x,y) << '\n';
}
}
空间/时间复杂度
先来算空间复杂度。
长度为 \(n\) 的线段分裂成两段后,每段长度都减半,直到每段长度都为一。可以粗略估计占了大约 \(n + \dfrac{n}{2} + \dfrac{n}{4} + ... + 1\) 个下标。数学敏感的人可能知道,这接近于 \(2n\)。但注意,千万不能只开 \(2n\) 的内存,不然叶子结点访问儿子时会越界。所以请记得开四倍空间。(作者就这么挂过)
然后算时间复杂度。区间加其实和区间查询的复杂度是一样的(区间加只多了个 \(\mathcal{O(1)}\) 的懒标记),而如果区间查询中,大块的都被一起加了,只有最多两个能扫到叶子结点。因此我们估计复杂度也不是很高的。实际上,它的复杂度约等于 \(\mathcal{O(\log n)}\)(常数较大),但也是很不错的复杂度了。
总结:线段树是很多题目的基础,在OI也是一个重要的算法。需要每一步都理解透彻。
练习题
这题大致意思是区间异或,区间求和。上面的线段树只能实现区间加。这里注意的是,线段树不仅可以区间加,还能区间与、区间开根、区间取模、区间异或......而区间加只是一个最简单的例子之一。同样,区间求和也可以变成区间最大值或最小值。甚至区间最大子段和也能实现。所以线段树是最受欢迎的算法,没有之一。
回到正题。我们如何维护区间异或呢?很简单。在上面的代码中,有这么一句话:tr[x].sum += (r - l + 1) * k;
我们考虑这一段全部异或会发生什么。神奇的事情出现了,更新后的 \(sum\) 似乎就等于区间的长度减去更新前的 \(sum\)(因为这两个结果相加就是区间的长度)。所以,我们把上面那句话改成 tr[x].sum = (tr[x].ye - tr[x].ze + 1 - tr[x].sum) 就行了。记得将 \(\text{pushdown}\) 的下传和输入也改一下。其实理论上这就是一个双倍经验。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号