AC 自动机

AC 自动机（简单版）的题目传送门

暴力思路

做 \(n\) 遍 KMP，复杂度 \(\mathcal{O}(n|t|)\)。

但我们发现有些模式串有着共同的后缀，或共同的前缀，我们或许可以运用这一点，进行优化？

然后 AC 自动机就诞生了。

本质是字典树

把 \(n\) 个串转换为一棵树，这棵树叫做字典树。因为树是一个整体，所以在之后更加方便操作。另外用一个数组来存储字符串末尾的位置。

void insert(string s)
{
    int xx = 0;
    for(int i = 0;i < s.size();i ++)
    {
        char p = s[i];
        p -= 96;
        if(!trie[xx][p])trie[xx][p] = ++id;//没有结点则新建
        xx = trie[xx][p];//跳到下一个结点
    }
    if(xx > 0)ansd[xx] ++;//在末尾位置加1
}

没怎么看懂？给你一张图：

e
he
her
she
shr
son

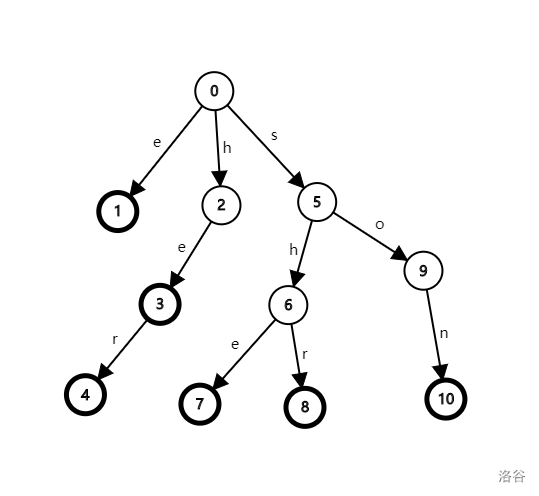
然后建树就完了。

当然只有这些是不够的，接下来就是它的真正魅力——建回跳边和转移边。

建边

我们要找到每一个点的下一个后继在哪里，否则你匹配文本串匹配到一个地方时，无法转移了——就比如，文本串叫 shson，你到第三个字符就发现无路可走。为了避免这种情况发生，我们需要新建转移边。

到底转移到哪里呢？为了搞清楚这个问题，我们还需要引入一个边——回跳边。这相当于 KMP 算法中的 nxt 数组但又不完全一样，回跳边指的是当前节点的最长后缀。

我们用 \(hui\) 数组来表示回跳边的终点。那么，对于一个结点 \(u\)，它有一个儿子 \(v\)，中间连的边为字符 \(c\)，那么 \(hui_v\) 就等于 \(trie_{hui_x,c}\)。

很多人会有一个疑问：为啥是这个结点？

这个理解其实不难：因为 \(hui_u\) 指向的就是从 \(0\) 号结点到 \(u\) 结点的最长后缀所指结点，那么同时再加个字符 \(c\)，依然还是最长后缀。

那么如果 \(u\) 没有一条字符 \(c\) 连向儿子的边呢？

这个时候，结点 \(u\) 就要自己转移，就是 \(trie_{u,c} = trie_{hui_u,c}\)。

比如，上图的 \(7\) 号结点就要向 \(4\) 号结点连一个字符为 \(r\) 的边，\(6\) 号结点要向 \(trie_{2,s}\) 号结点连一个字符为 \(s\) 的边（因为 \(hui_6 = 2\)）。

可能有些人还是有点懵。这里可以说明一下：转移边相当于树边，是退无可路下的紧急转移；回跳边是为了搜索所有有相同后缀的模式串。

然后就是此部分的代码。我们用 \(\text{bfs}\) 遍历整棵树，当访问到儿子时将它推进队列。

void build()
{
    queue<int>q;
    for(int i = 1;i <= 26;i ++)if(trie[0][i])q.push(trie[0][i]);//推进队列
    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        for(int i = 1,x;i <= 26;i ++)
        {
            x = trie[t][i];//儿子
            if(x)hui[x] = trie[hui[t]][i],q.push(x);//如果有，则儿子建立回跳边
            else trie[t][i] = trie[hui[t]][i];//没有父亲建边
        }
    }
}

查询

查询就是绝杀。

我们设置两个指针 \(j,k\)，\(k\) 沿着树边或转移边走，\(k\) 赋值为 \(j\) 后沿转移边走把所指的结点全部访问一遍，如果有该节点有模式串终结点的位置则把答案记录到 \(ans\) 中。于是这题就做完了。

但是直接暴力搞可能会 TLE，那么我们用记忆化搜索的思想，每次访问之后把那个结点标记为 \(-1\)，这样就能确保每个模式串最多只会访问一次了。

int query(string t)
{
    int ans = 0;
    for(int i = 0,j = 0;i < t.size();i ++)
    {
        j = trie[j][t[i] - 96];//沿着树边或转移边走
        for(int k = j;k && ansd[k] >= 0;k = hui[k])//未访问
            ans += ansd[k],ansd[k] = -1;//已访问
    }
    return ans;
}

下面是完整代码。

#include <iostream>
#include <queue>
using namespace std;
int n,trie[1000005][27],id,ansd[1000005],hui[1000005];
void insert(string s)
{
    int xx = 0;
    for(int i = 0;i < s.size();i ++)
    {
        char p = s[i];
        p -= 96;
        if(!trie[xx][p])trie[xx][p] = ++id;
        xx = trie[xx][p];
    }
    if(xx > 0)ansd[xx] ++;
}
void build()
{
    queue<int>q;
    for(int i = 1;i <= 26;i ++)if(trie[0][i])q.push(trie[0][i]);
    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        for(int i = 1,x;i <= 26;i ++)
        {
            x = trie[t][i];
            if(x)hui[x] = trie[hui[t]][i],q.push(x);
            else trie[t][i] = trie[hui[t]][i];
        }
    }
}
int query(string t)
{
    int ans = 0;
    for(int i = 0,j = 0;i < t.size();i ++)
    {
        j = trie[j][t[i] - 96];
        for(int k = j;k && ansd[k] >= 0;k = hui[k])
            ans += ansd[k],ansd[k] = -1;
    }
    return ans;
}
string s[1000005],t;
int main()
{
    cin >> n;
    for(int i = 1;i <= n;i ++)cin >> s[i],insert(s[i]);
    cin >> t;
    build();
    cout << query(t);
}

时间复杂度分析：最多只会多建造 \(26 \times \sum\limits_{i = 1}^n |s_i|\) 条边，而每个结点只会访问一次，所以复杂度就是 \(\mathcal{O}(26n)\)。

练习

换一个题目：简单版 II

不难发现模式串最多只有 \(70\)，所以最多树的深度 \(70\) 层。所以不用记忆化搜索，直接计数每个结点访问的次数即可。

【模板】AC 自动机

这题不能使用记忆化搜索，而模式串长度又很长，怎么办呢？

我们先记录一下 \(j\) 指针移动的位置，最后再统一处理。统一处理的时候，如果一个结点被访问过，直接沿回跳边回跳即可，并累加和。最后输出累加的和即可。

代码（部分）

void query(string t)
{
    int ans = 0;
    for(int i = 0,j = 0;i < t.size();i ++)
    {
        j = trie[j][t[i] - 96];
        df[j] ++;//df是标记数组
    }
}

for(int i = 200004;i >= 0;i --)
{
    if(df[i])
    {
        for(int k = i,u = df[i];k;df[k] = 0,k = hui[k],u += df[k])//u是累加和
            for(int l = 0;l < ansd[k].size();l ++)ji[ansd[k][l]] += u;//ji是答案数组
    }
}

感谢观看！！！（qwq）