机器学习算法-第一篇随记

1.无监督学习还可以减少数据特征的维度，以便我们可以使用二维或三维图形更加直观地展示数据信息。

2.机器如一个机械的学生一样，只能通过尝试答对（最小化损失）大量的习题（已知样本）来学习知识（模型参数

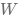），并期望用学习到的知识（模型参数 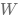），组成完整的模型 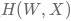，回答不知道答案的考试题（未知样本）。

3.评价函数==损失函数

4.深度学习与机器学习在理论结构上是一致的：即模型假设、评价函数和优化算法，根本差别在于假设的复杂度

5.人工神经网络包括多个神经网络层，如卷积层、全连接层、LSTM等又包括很多神经元，超过三层的非线性神经网络都可以被称为深度神经网络。神经网络非常适合学习样本数据的内在规律和表示层次，对文字、图像和语音任务有很好的适用性。

6.神经网络并没有那么神秘，它的本质是一个含有很多参数的“大公式”。

7.nlp的长期短期记忆模型LSTM：可以分为组网模块、梯度下降的优化模块和预测模块等。

8.对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为回归任务和分类任务。

9.神经网络的标准结构中每个神经元由加权和与非线性变换构成，然后将多个神经元分层的摆放并连接形成神经网络。

 

 

10.数据处理包含五个部分：数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。数据预处理后，才能被模型调用。
'''绝对地址、相对地址
如果引用绝对地址需加 r'绝对地址'

path.append(r'E:\Downloads\绝对地址\demo') # 添加路径

相对地址

../ 表示当前文件所在的目录的上一级目录

./ 表示当前文件所在的目录(可以省略)

/ 表示当前站点的根目录(域名映射的硬盘目录)
'''
'''
numpy.fromfile

numpy.fromfile(file, dtype=float, count=-1, sep='', offset=0)

从文本或二进制文件中的数据构造一个数组。

读取已知数据类型的二进制数据以及解析简单格式化的文本文件的一种高效方法。使用tofile方法写入的数据可以使用此函数读取。
'''

11.处于曲线极值点时的斜率为0，即函数在极值点处的导数为0。那么，让损失函数取极小值-------》等价于损失函数对w和b的导数为0。---但只适合线性回归这样简单的任务，如果模型中含有非线性变换，或者l不是均分误差。

12.在现实中存在大量的函数正向求解容易，反向求解较难，被称为单向函数。

13.这种函数在密码学中有大量的应用，密码锁的特点是可以迅速判断一个密钥是否是正确的(已知x，求y 很容易)，但是即使获取到密码锁系统，无法破解出正确的密钥是什么（已知y，求x很难）。

14.他看不见坡谷在哪（无法逆向求解出$Loss&导数为0时的参数值），但可以伸脚探索身边的坡度（当前点的导数值，也称为梯度）。那么，求解Loss函数最小值可以“从当前的参数取值，一步步的按照下坡的方向下降，直到走到最低点”实现。这种方法笔者个人称它为“盲人下坡法”。哦不，有个更正式的说法“梯度下降法”。

15.Numpy库的广播机制，一方面可以扩展参数的维度，代替for循环来计算1个样本对从w0 到w12 的所有参数的梯度；另一方面可以扩展样本的维度，代替for循环来计算样本0到样本403对参数的梯度。

16.参数需要向梯度的反方向移动。

17.特征输入归一化后，不同参数输出的Loss是一个比较规整的曲线，学习率可以设置成统一的值 ；特征输入未归一化时，不同特征对应的参数所需的步长不一致，尺度较大的参数需要大步长，尺寸较小的参数需要小步长，导致无法设置统一的学习率。

18.由于参数每次只沿着梯度反方向更新一点点，因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数，这种方法被称作随机梯度下降法（Stochastic Gradient Descent，SGD）。

通过大量实验发现，模型对最后出现的数据印象更加深刻。训练数据导入后，越接近模型训练结束，最后几个批次数据对模型参数的影响越大。为了避免模型记忆影响训练效果，需要进行样本乱序操作。

import matplotlib.pyplot as plt
import numpy as np

# 读入训练数据
datafile = 'F:\data\housing.data'
data = np.fromfile(datafile, sep=' ')
#print(data) [6.320e-03 1.800e+01 2.310e+00 ... 3.969e+02 7.880e+00 1.190e+01]


# 2.数据形状变换
# 读入之后的数据被转化成1维array，其中array的第0-13项是第一条数据，第14-27项是第二条数据，以此类推....
# 这里对原始数据做reshape，变成N x 14的形式
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE' , 'DIS' , 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# print(feature_num)  # feature_num=14
data = data.reshape([data.shape[0] // feature_num, feature_num])
# print(data.shape)  # (506, 14)
#print(data[0])  # 对应数据集第一行14个数据

# 3.数据集划分
ratio = 0.8  # 所有数据中作为训练集的比例
offset = int(data.shape[0] * ratio)
training_data = data[:offset]  # 切片操作，从第0个到offset-1个
#print(training_data.shape)  # (404, 14)

# 4.数据归一化处理
# 计算train数据集的最大值，最小值，平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), training_data.sum(axis=0) / training_data.shape[0]
#print(maximums,minimums,avgs) #得到每一列的最大值、最小值、平均值


# 对数据进行归一化处理
for i in range(feature_num):
    # print(maximums[i], minimums[i], avgs[i]) #88.9762 0.00632 1.9158993069306929
    data[:,i] = (data[:,i] - minimums[i]) / (maximums[i] - minimums[i]) # 所有的值都在0-1之间了

#print(data[0]) #[0.         0.18       0.07344184 0.         0.31481481 0.57750527

# 5.封装成load data函数
# 封装成函数的目的是方便以后的模型调用

def load_data():
    # 从文件导入数据
    datafile = 'F:\data\housing.data'
    data = np.fromfile(datafile, sep=' ')
    # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
    feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
                     'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
    feature_num = len(feature_names)
    # 将原始数据进行Reshape，变成[N, 14]这样的形状
    data = data.reshape([data.shape[0] // feature_num, feature_num])
    # 将原数据集拆分成训练集和测试集
    # 这里使用80%的数据做训练，20%的数据做测试
    # 测试集和训练集必须是没有交集的
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    # 计算训练集的最大值，最小值，平均值
    maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
                               training_data.sum(axis=0) / training_data.shape[0]
    # 对数据进行归一化处理
    for i in range(feature_num):
        # print(maximums[i], minimums[i], avgs[i])
        data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
    # 训练集和测试集的划分比例
    training_data = data[:offset]
    test_data = data[offset:]
    return training_data, test_data


# 获取数据
training_data, test_data = load_data()
x = training_data[:,: -1] # 去掉最后一列数据，每组数据变成13个
y = training_data[:, -1:] # 最后一列数据


class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，
        # 此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.rand(num_of_weights,1)
        self.b = 0.

    def forward(self,x):
        z = np.dot(x,self.w) + self.b
        return  z

    def loss(self, z ,y):
        error = z - y
        # num_samples = error.shape[0]
        cost = error * error
        # print('每个样本的cost',cost)
        #计算损失时需要把每个样本的损失都考虑到,对单个样本的损失函数进行求和，并除以样本总数
        # cost = np.sum(cost) / num_samples
        cost = np.mean(cost)
        return cost

    def gradient(self, x, y):
        z = self.forward(x)
        N = x.shape[0]
        gradient_w = (z - y) * x #gradient_w的每一行代表了一个样本对梯度的贡献
        gradient_w = 1.0 / N * np.mean(gradient_w,axis=0) #axis = 0 表示列方向,使用np.mean函数的时候消除了第0维, gradient_w的形状是(13,)
        gradient_w = gradient_w[:, np.newaxis]  # 将gradient_w的维度也设置为(13, 1)
        gradient_b = (z - y)
        gradient_b = 1. / N * np.mean(gradient_b)
        return gradient_w, gradient_b

    def update(self, gradient_w, gradient_b, lr = 0.01):
        self.w = self.w - lr * gradient_w
        self.b = self.b - lr * gradient_b

    def train(self, train_data, num_epoches, batch_size = 10, lr = 0.01):
        n = len(train_data)
        losses = []
        for epoch_id in range(num_epoches):
            # 在每轮迭代开始之前，将训练数据的顺序随机的打乱，
            # 然后再按每次取batch_size条数据的方式取出
            np.random.shuffle(train_data)
            # 将训练数据进行拆分，每个mini_batch包含batch_size条的数据
            mini_batches = [train_data[k:k + batch_size] for k in range(0, n, batch_size)]
            for iter_id, mini_batch in enumerate(mini_batches):
                x = mini_batch[:, :-1]  # 去掉最后一列数据，每组数据变成13个
                y = mini_batch[:, -1:]  # 最后一列数据
                z = self.forward(x)
                L = self.loss(z,y)
                gradient_w, gradient_b = self.gradient(x, y)
                self.update(gradient_w, gradient_b, lr)
                losses.append(L)

                print('epoch{:3d} / iter {:3d},loss = {:.4f}'.format(epoch_id, iter_id, L))
        return losses

# 获取数据
train_data, _ = load_data()

#创建网络
net = Network(13)
#启动训练
losses = net.train(train_data, num_epoches = 50, batch_size = 100, lr = 0.01)

#画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x,plot_y)
plt.show()


#随机梯度下降加快了训练过程，但由于每次仅基于少量样本更新参数和计算损失，所以损失下降曲线会出现震荡。


# w= net.w
# print(w)
# x1 = x[0:3]
# y1 = y[0:3]
# z = net.forward(x)
# loss = net.loss(z,y)
# # print(x1)
# # print('z',z)
# # #print(y1)
# #print('loss',loss)
# gradient_w = (z-y) * x  #gradient_w的每一行代表了一个样本对梯度的贡献
# gradient_w = np.mean(gradient_w, axis=0) #使用np.mean函数的时候消除了第0维, gradient_w的形状是(13,)
# gradient_w = gradient_w[:, np.newaxis] #将gradient_w的维度也设置为(13, 1)
# print('gradient_w shape {}'.format((gradient_w.shape)))
# print(gradient_w)