第04次作业-树

1.学习总结

1.1树结构思维导图

 

 

1.2 树结构学习体会

　　对树结构认识：树是由一个集合以及在该集合上定义的一种关系构成的，是一种重要的非线性数据结构。

　　困难：有些对树操作中的递归算法理解有点困难，和各种非递归的遍历方法。

　　树结构可以解决的问题：表达式的转换，求树的带权路径长度，并查集问题等等。

2.PTA实验作业

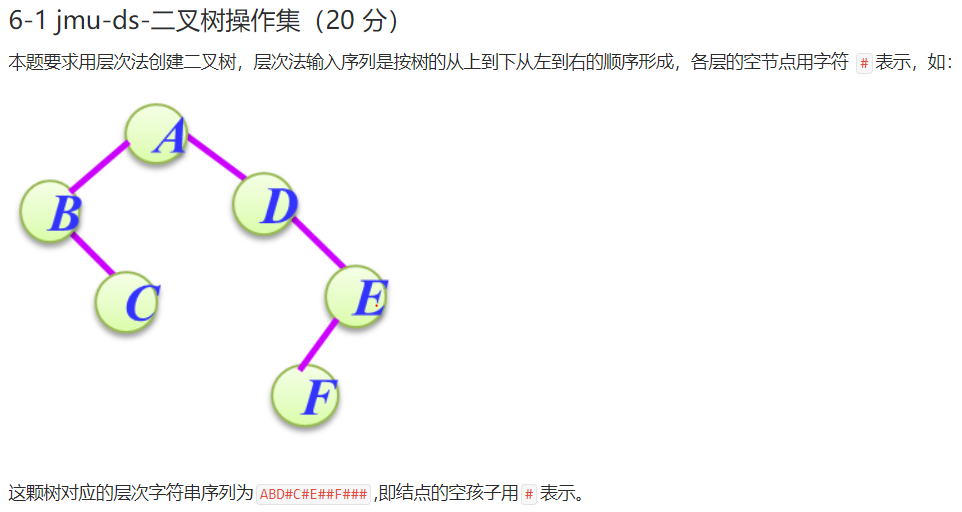
2.1 题目1：6-1 jmu-ds-二叉树操作集

2.2 设计思路（伪代码或流程图）

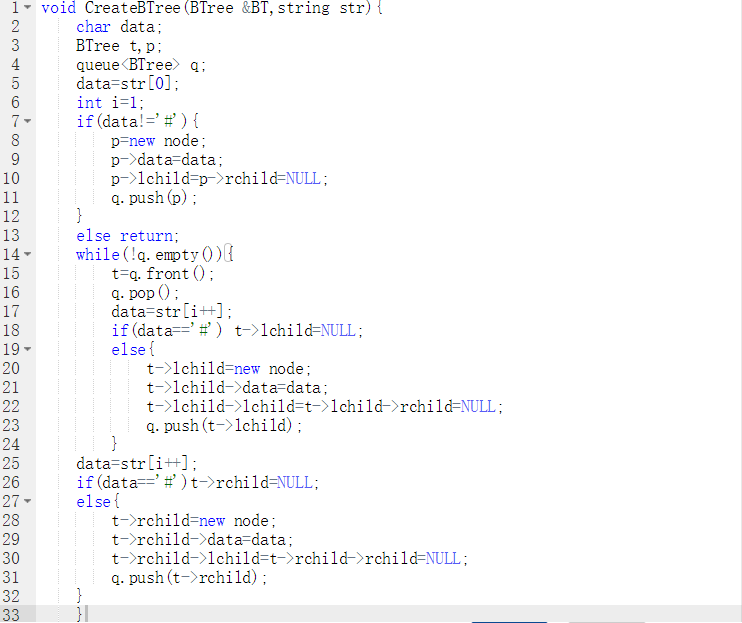
void CreateBTree(BTree &BT,string str)//层次建立二叉树
{
    定义树形指针 t;
    queue<BTree> q;
    if(str[0]不为'#'){
       建立根结点p；
       p->lchild和p->rchild分别为空；
       将p入队
    }
    else return;
    while(队列非空){
        q出队，并将元素赋t；
        if(str[i]为'#') t->lchild为空;
        else{
            建立t的右结点t->lchild；
            将t->lchild入队；
        }
        i++；
    if(str[i]为'#')t->rchild为空;
    else{
            建立t的右结点t->rchild；
            将r->lchild入队；
　　　　　}
　　}
　　BT=p；
}

2.3 代码截图

2.4 PTA提交列表说明

格式错误是我在头个输出前多了个空格

解决：用了题目给的全局变量bool flag=true；通过他控制头个空格的输出。

 

2.1 题目2：6-4 jmu-ds-表达式树

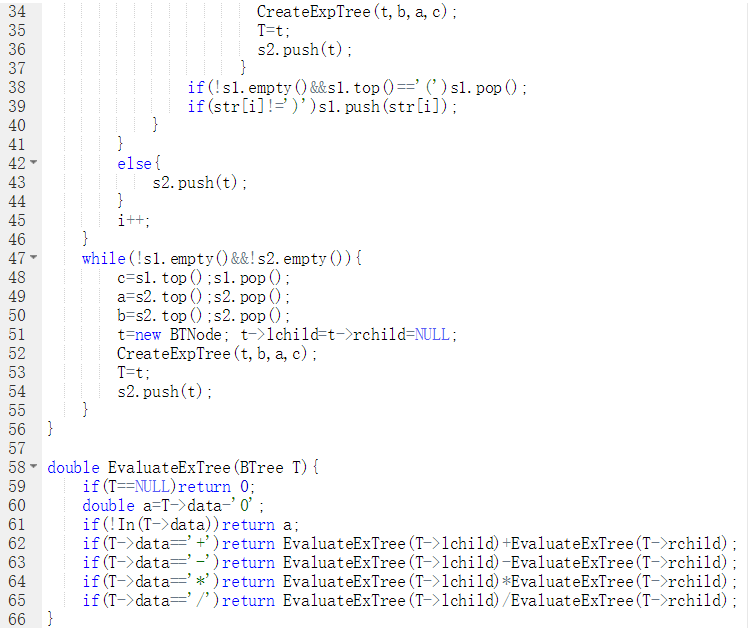
2.2 设计思路（伪代码或流程图）

void InitExpTree(BTree &T,string str)
{
    建立字符型的栈 s1;
    建立树型的栈 s2;//s1存放字符，s2存放数字
    int i=0;
    char c,f;
    BTree t;//根结点
    BTree a,b;//子结点
    if(str[0]为'\0')return;
    while(str[i]不为'\0'){
            
            if(若‘/’后是否为‘0’){
                输出"divide 0 error!"
                T为空;
                exit(0);
            }
        建立树结点t，并将str[i]赋给该结点
        if(str[i]为运算符){

            if(栈s1为空){
                str[i]入栈
                i++;
                continue;
            }
            比较str[i],s1.top()的优先级，并赋给f；
           if((f=='>'||str[i]=='('||s1.top()=='(')&&str[i]!=')')s1.push(str[i]);
            else if(f=='<'||str[i]==')'){
                while(!s1.empty()&&s1.top()!='('){
                         将s1的栈顶元素给c并出栈
                         将s2的栈顶元素给b并出栈
                         将s2的栈顶元素给a并出栈
                         建立一个以c为根结点，b和c为子结点的树
                        T=t;
                        将t入栈s2；
                      }
                if(!s1.empty()&&s1.top()=='(')s1出栈;
                if(str[i]!=')')str[i]直接入栈到s1；
            }
        }
        else{
            将非运算符入栈到s2;
        }
        i++;
    }
    while(若栈s1和s2都不为空){
        将s1的栈顶元素给c并出栈
        将s2的栈顶元素给b并出栈
        将s2的栈顶元素给a并出栈
        建立一个以c为根结点，b和c为子结点的树
        T=t;
        将t入栈s2；
    }
}

double EvaluateExTree(BTree T){
    if(T==NULL)return 0;
    double a=T->data-'0';
    if(若T->data不为运算符)return a;
    if(T->data=='+')return EvaluateExTree(T->lchild)+EvaluateExTree(T->rchild);
    if(T->data=='-')return EvaluateExTree(T->lchild)-EvaluateExTree(T->rchild);
    if(T->data=='*')return EvaluateExTree(T->lchild)*EvaluateExTree(T->rchild);
    if(T->data=='/')return EvaluateExTree(T->lchild)/EvaluateExTree(T->rchild);
}  

2.3 代码截图

2.4 PTA提交列表说明

错误点：1.遇到除0，输出divide 0 error!，但我不知道如何直接退出

　　2.括号的优先级判断错误，及遇到括号时的操作

解决：第一点，通过百度知道了exit(0)，可以直接退出程序

　第二点，我没明白题目所给的括号的优先级的表示，因此我想只要遇到‘（’就入栈，遇到‘）’就将运算符出栈直到栈顶为‘（’。　　ps：不过看了同学的代码，才知道我这样确实是麻烦了，我没完美运用题目所给的条件。。。

 

 

 

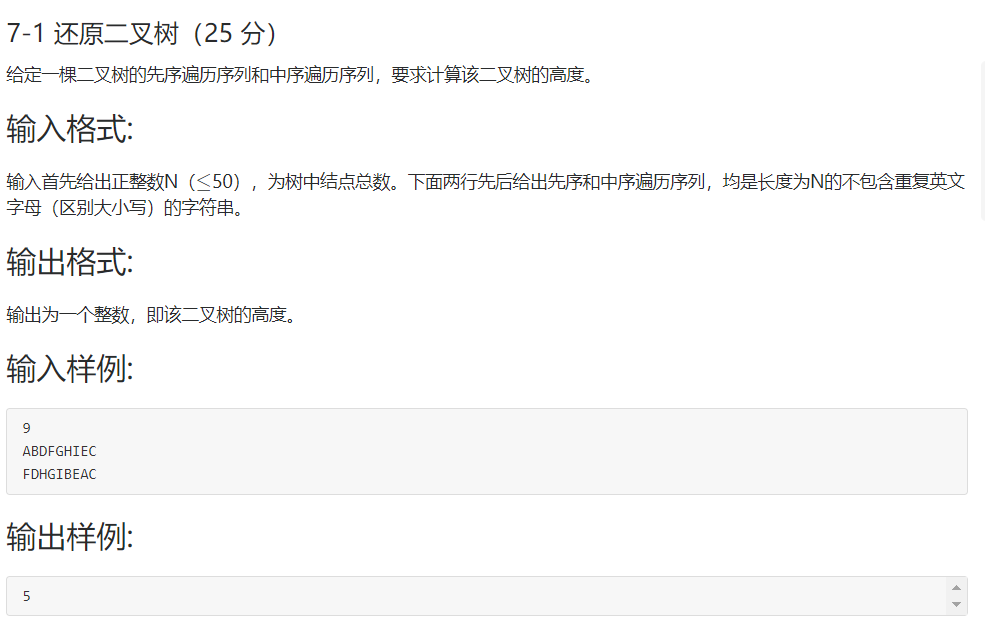
2.1 题目3：7-1 还原二叉树（25 分）

 

2.2 设计思路（伪代码或流程图）

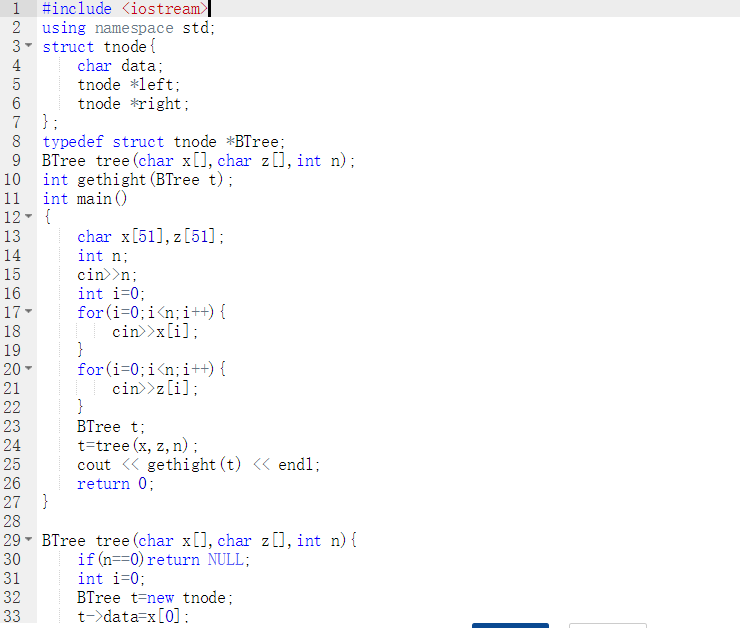
BTree tree(char x[],char z[],int n)//用递归算法还原二叉树
{
    if(若n为0)返回空;
    int i=0;
    建立树结点t，并将先序x[0]给t->data;
    for(i=0;i<n;i++){
        if(中序z[i]==先序的第一个元素x[0]){
           跳出循环；
        }
    }
    //以位置i为分界进行左右还原
    对t的左子树进行还原t->left=tree(x+1,z,i);
    对t的右子树进行还原t->right=tree(x+i+1,z+i+1,n-i-1);
    return t;
}
int gethight(BTree t)//求二叉树高
{
    int hl,hr,maxh;
    if(t不为空){
        求左子树hl的高度
        求右子树hr的高度
        对比hl和hr,将高度大的赋给maxh
        return maxh+1;
    }
    else return 0;
}

 

2.3 代码截图

 

 

2.4 PTA提交列表说明

 

 

 

3.截图本周题目集的PTA最后排名

3.1 PTA排名截图

3.2 我的总分：2.5

4. 阅读代码（必做）

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

#define N 10         // 带编码字符的个数，即树中叶结点的最大个数
#define M (2*N-1)    // 树中总的结点数目

class HTNode{        // 树中结点的结构
public: 
    unsigned int weight;
    unsigned int parent,lchild,rchild;
};                    

class HTCode{
public:
    char data;      // 待编码的字符
    int weight;     // 字符的权值
    char code[N];   // 字符的编码
};

void Init(HTCode hc[], int *n){
// 初始化，读入待编码字符的个数n，从键盘输入n个字符和n个权值
    int i;
    printf("input n = ");
    scanf("%d",&(*n));

    printf("\ninput %d character\n",*n);
     
    fflush(stdin);
    for(i=1; i<=*n; ++i)
        scanf("%c",&hc[i].data);

    printf("\ninput %d weight\n",*n);
    
    for(i=1; i<=*n; ++i)
        scanf("%d",&(hc[i].weight) );
    fflush(stdin);
}//

void Select(HTNode ht[], int k, int *s1, int *s2){
// ht[1...k]中选择parent为0，并且weight最小的两个结点，其序号由指针变量s1，s2指示
    int i;
    for(i=1; i<=k && ht[i].parent != 0; ++i){ 
        ; ;
    }
    *s1 = i;

    for(i=1; i<=k; ++i){
        if(ht[i].parent==0 && ht[i].weight<ht[*s1].weight)
            *s1 = i;
    }

    for(i=1; i<=k; ++i){
        if(ht[i].parent==0 && i!=*s1)
            break;
    }
    *s2 = i;

    for(i=1; i<=k; ++i){
        if(ht[i].parent==0 && i!=*s1 && ht[i].weight<ht[*s2].weight)
            *s2 = i;
    }
}

void HuffmanCoding(HTNode ht[],HTCode hc[],int n){
// 构造Huffman树ht，并求出n个字符的编码
    char cd[N];
    int i,j,m,c,f,s1,s2,start;
    m = 2*n-1;
    
    for(i=1; i<=m; ++i){
        if(i <= n)
            ht[i].weight = hc[i].weight;
        else
            ht[i].parent = 0;
        ht[i].parent = ht[i].lchild = ht[i].rchild = 0;
    }

    for(i=n+1; i<=m; ++i){
        Select(ht, i-1, &s1, &s2);
        ht[s1].parent = i;
        ht[s2].parent = i;
        ht[i].lchild = s1;
        ht[i].rchild = s2;
        ht[i].weight = ht[s1].weight+ht[s2].weight;
    }

    cd[n-1] = '\0';

    for(i=1; i<=n; ++i){
        start = n-1;
        for(c=i,f=ht[i].parent; f; c=f,f=ht[f].parent){
            if(ht[f].lchild == c)
                cd[--start] = '0';
            else
                cd[--start] = '1';
        }
        strcpy(hc[i].code, &cd[start]);
    }
}


int main()
{
    int i,m,n,w[N+1];
    HTNode ht[M+1];
    HTCode hc[N+1];
    Init(hc, &n);     // 初始化
     HuffmanCoding(ht,hc,n);   // 构造Huffman树，并形成字符的编码

    for(i=1; i<=n; ++i)  
        printf("\n%c---%s",hc[i].data,hc[i].code);  
    printf("\n");

    return 0;
}

 

代码地址：https://blog.csdn.net/shuangde800/article/details/7341289

代码功能：建立哈夫曼树并转码

选择原因：代码简洁，学习到了哈夫曼树的构建，初步了解了C++中public的用法

5. 代码Git提交记录截图