计数类dp

AcWing 900. 整数划分

一个正整数 n 可以表示成若干个正整数之和，形如：n=n1+n2+…+nk，其中 n1≥n2≥…≥nk,k≥1。
我们将这样的一种表示称为正整数 n 的一种划分。
现在给定一个正整数 n，请你求出 n 共有多少种不同的划分方法。

输入格式

共一行，包含一个整数 n。

输出格式

共一行，包含一个整数，表示总划分数量。

由于答案可能很大，输出结果请对 109+7 取模。

数据范围

1≤n≤1000

输入样例:

5

输出样例：

7

思路

整数划分不考虑顺序
那么我们就将整数划分问题转化为完全背包问题
把要被划分的整数看成是容量为n的背包
物品体积分别为1,2,3......n
每种物品有无限个
求恰好装满背包的方案数

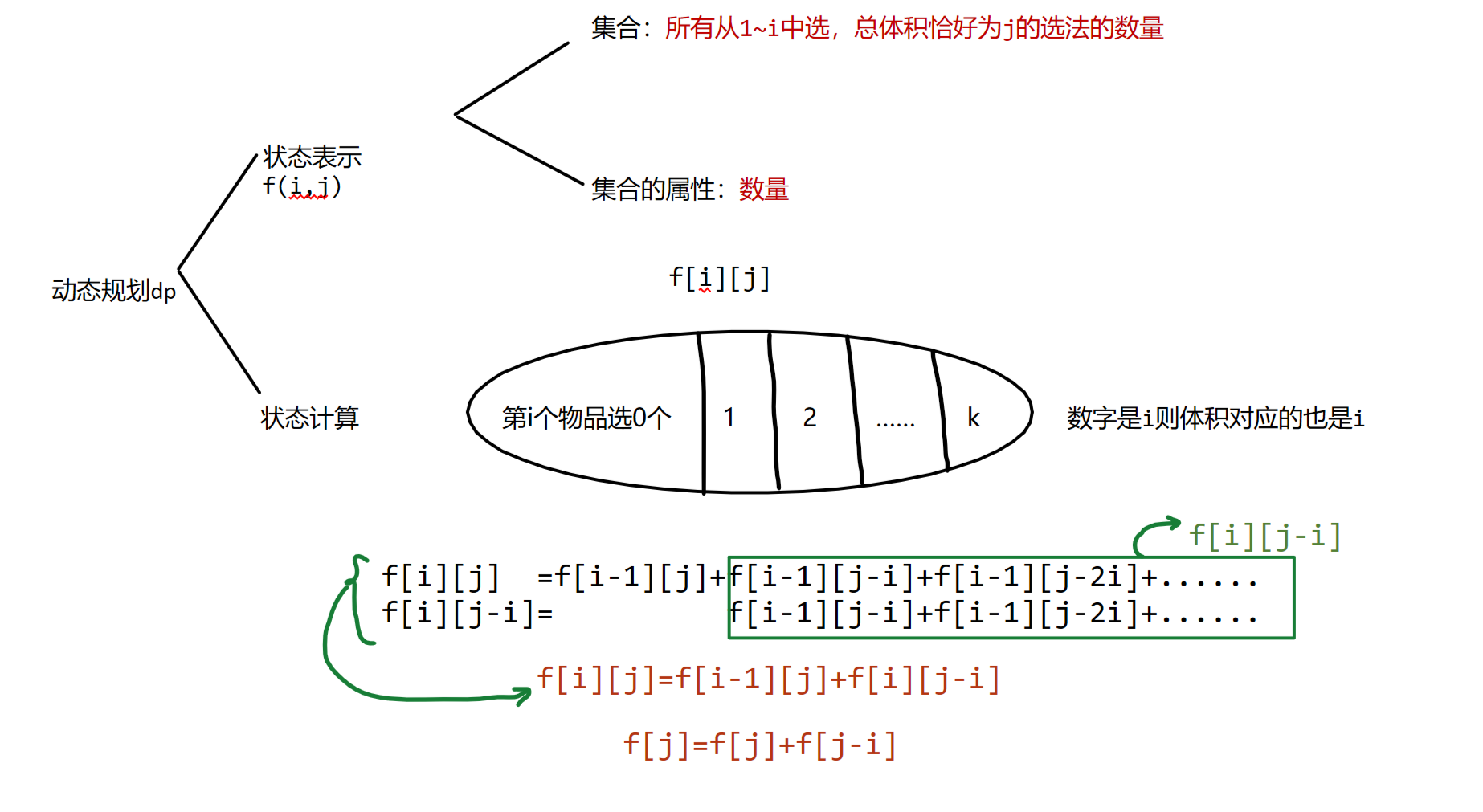
代码

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010 ,  mod = 1e9+7;

int n;
int f[N];
int main ()
{
    cin>>n;
    
    f[0]=1;
    for(int i=1;i<=n;i++)
       for(int j=i;j<=n;j++)
          f[j]=(f[j]+f[j-i])%mod;
          
    cout<<f[n]<<endl;
    return 0;
}