线性dp
数字三角形
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输入格式
第一行包含整数 n ,表示数字三角形的层数。
接下来 n 行,每行包含若干整数,其中第 i 行表示数字三角形第 i 层包含的整数。
输出格式
输出一个整数,表示最大的路径数字和。
数据范围
1≤n≤500 , −10000≤三角形中的整数≤10000
输入样例:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出样例:
30
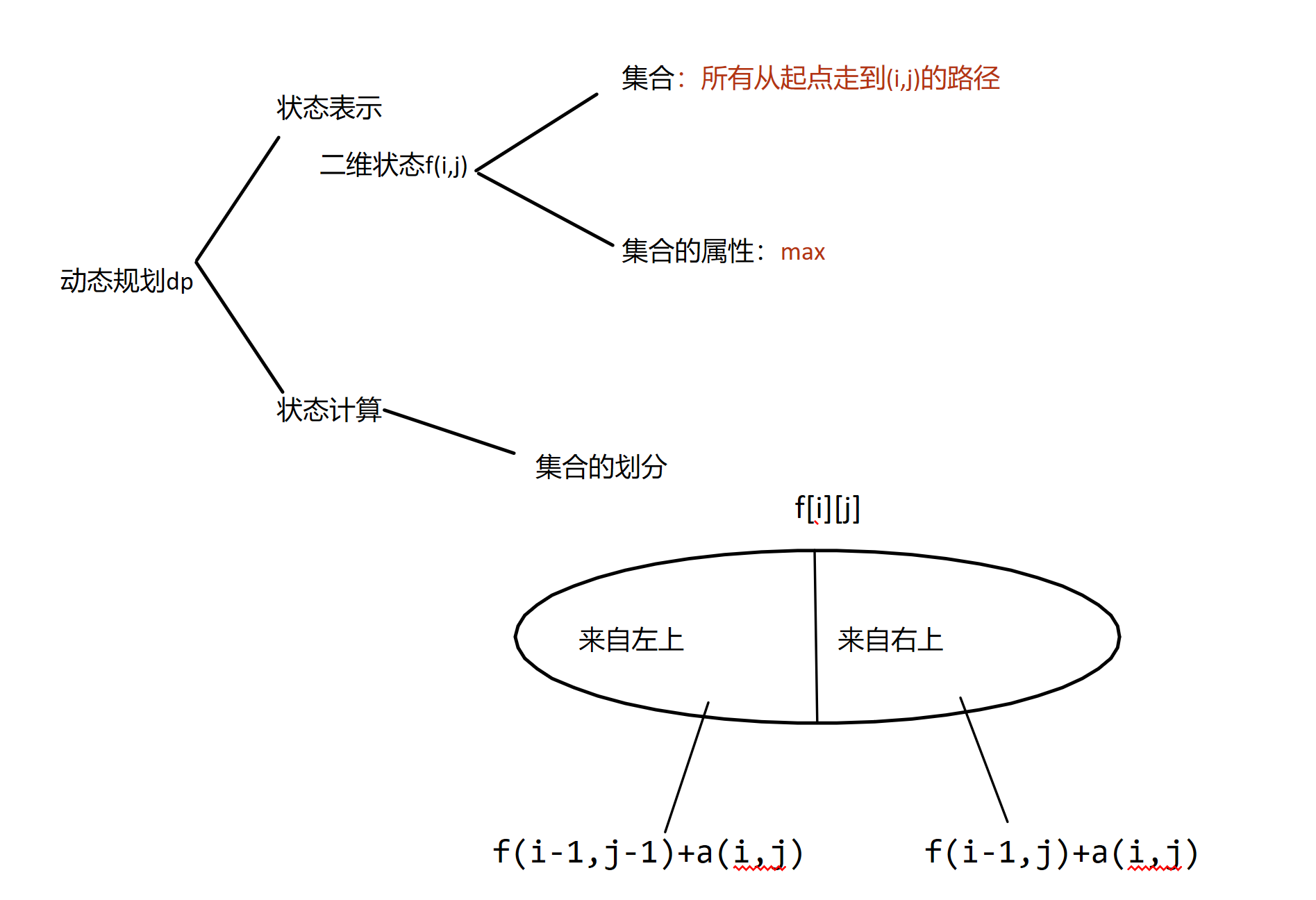
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int n ,INF=0x3f3f3f3f ;
int f[N][N],a[N][N];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=0;j<=i+1;j++) //因为有负数,所以应该将两边也设为-INF
f[i][j]=-INF;
f[1][1]=a[1][1];
for(int i=2;i<=n;i++)
for(int j=1;j<=i;j++)
f[i][j]=max(f[i-1][j]+a[i][j],f[i-1][j-1]+a[i][j]);
int res=-INF;
for(int i=1;i<=n;i++) res=max(res,f[n][i]);
cout<<res<<endl;
return 0;
}
最长上升子序列
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数 N 。
第二行包含 N 个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N≤1000 ,−109≤数列中的数≤109
输入样例:
7
3 1 2 1 8 5 6
输出样例:
4
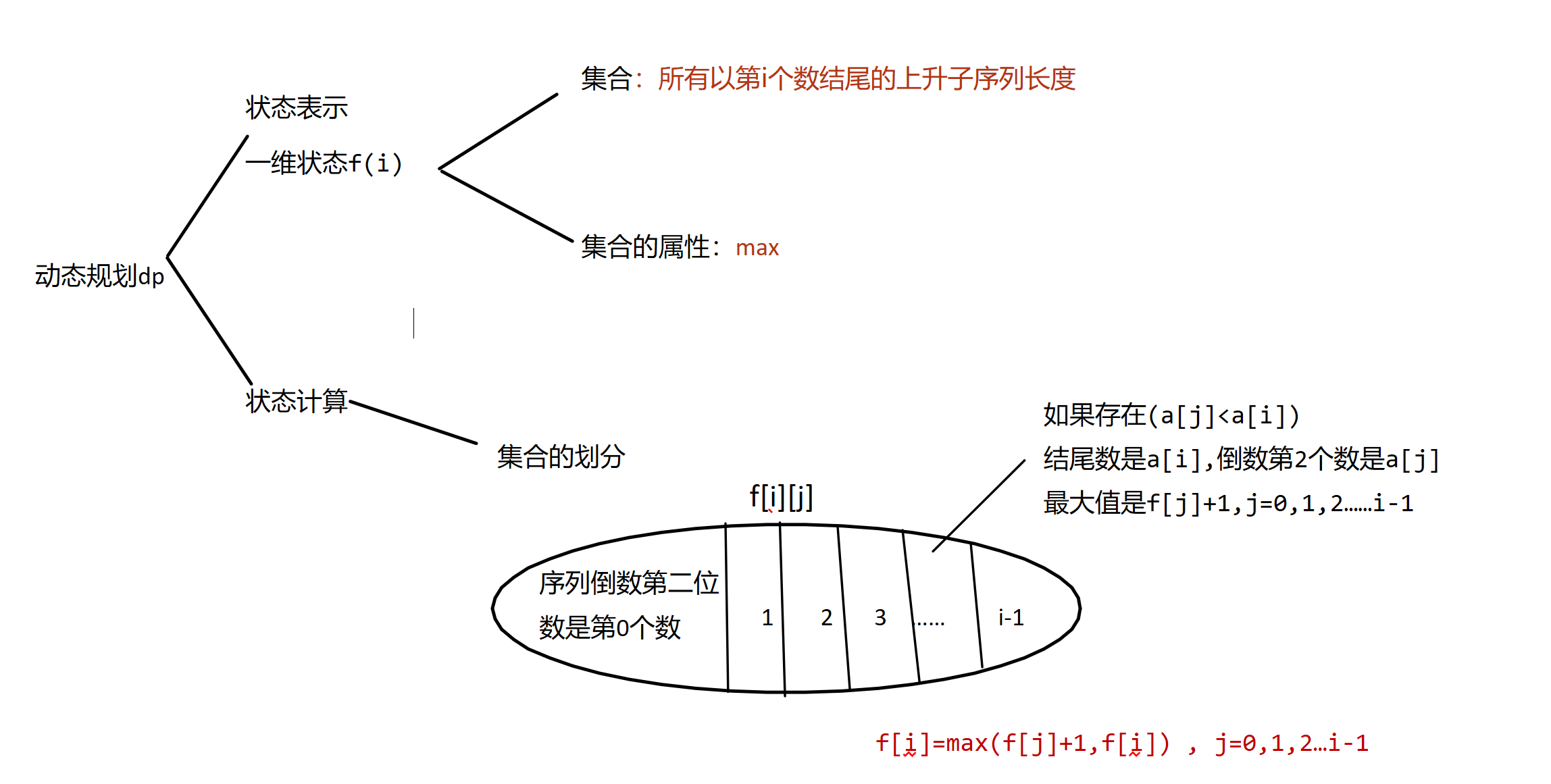
代码
#include <bits/stdc++.h>
using namespace std;
const int N =1010;
int f[N] , a[N];
int n ;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=0;j<i;j++)
if(a[j]<a[i])
f[i]=max(f[j]+1,f[i]);
}
int res=0;
for(int i=1;i<=n;i++) res=max(res,f[i]);
cout<<res<<endl;
return 0;
}
但是当数据范围变大时,就会TLE
如何优化呢?
7
3 1 2 1 8 5 6
能看出:可以接在3后面的一定可以接在1后面,那么3就没有存的必要了,
因为有1的上升子序列更长(小的适用范围更广)
假如求以a[i]结尾的最长上升子序列长度
应该把a[i]接到一个最大的小于a[i]的数(记为q[4])//二分
那么就不可能接到q[5](q[5]>=a[i])的上升子序列后面
直接把a[i]更新到q[5](储存所有长度是5的上升子序列的结尾)
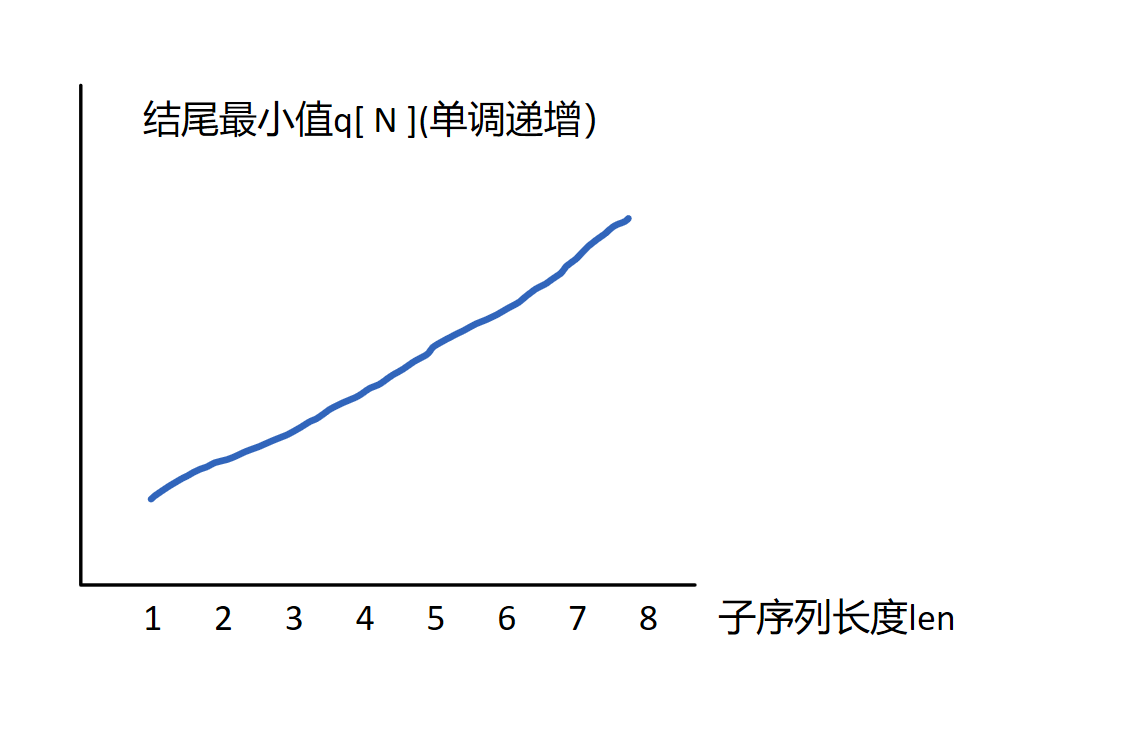
优化代码
#include <bits/stdc++.h>
using namespace std;
const int N =100010;
int q[N] , a[N];//q表示所有不同长度下上升子序列的最小值
int n ;
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
int len=0;
for(int i=0;i<n;i++)//二分找出小于a[i]的最大的数
{
int l=0,r=len;
while(l<r)
{
int mid = (l+r+1)>>1;
if(q[mid]<a[i]) l=mid;
else r=mid-1;
}
len=max(len,r+1);
q[r+1]=a[i];//把a[i]更新为目前长度+1的上升子序列的最小值
}
cout<<len<<endl;
return 0;
}
最长公共子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N 和 M
第二行包含一个长度为 N 的字符串,表示字符串 A
第三行包含一个长度为 M 的字符串,表示字符串 B
字符串均由小写字母构成
输出格式
输出一个整数,表示最大长度。
数据范围
1 ≤ N , M ≤ 1000
输入样例:
4 5
acbd
abedc
输出样例:
3
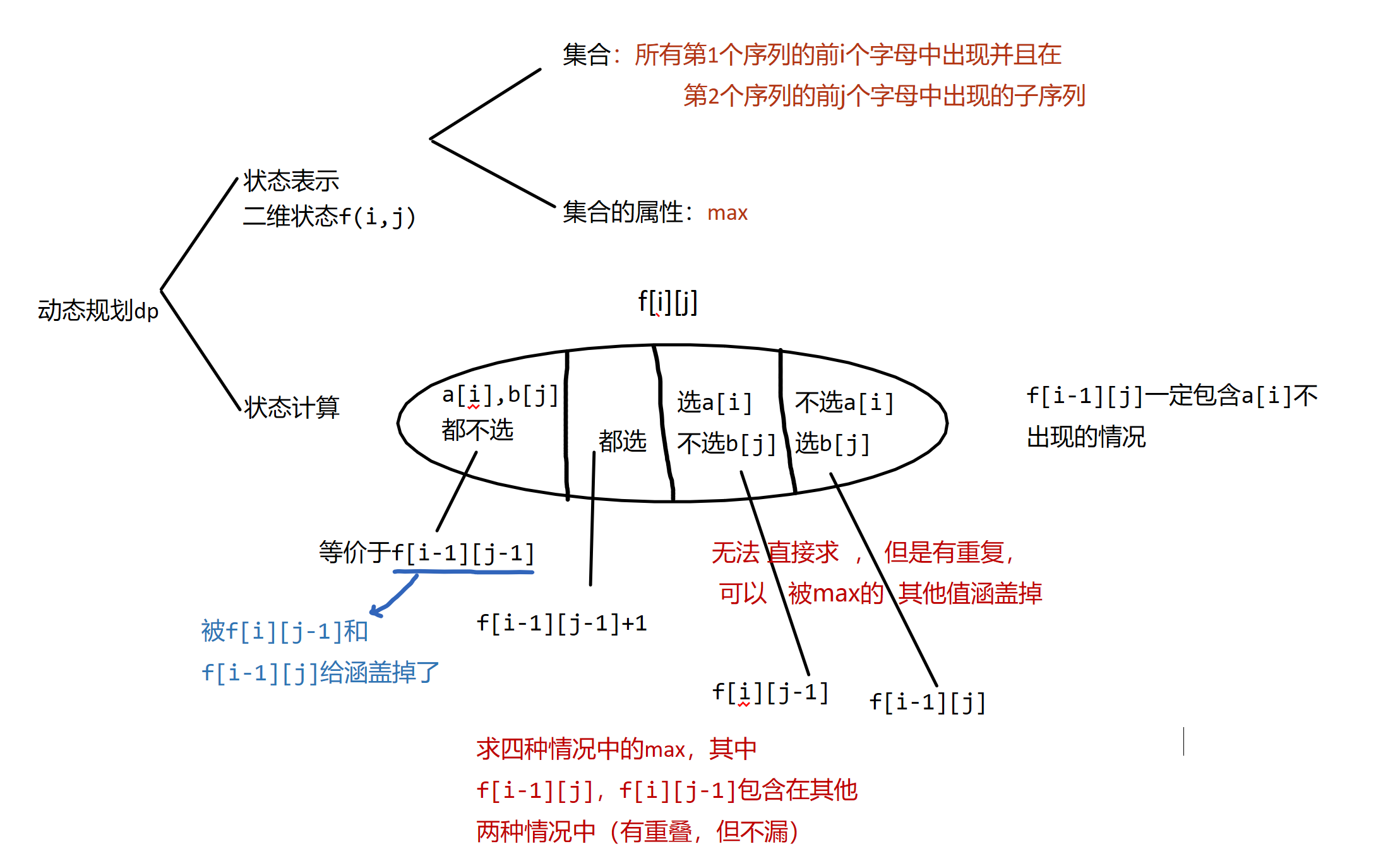
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
char a[N] , b[N];
int f[N][N];
int n ,m ;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int j=1;j<=m;j++) cin>>b[j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j])
f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
int res=0;
for(int i=1;i<=n;i++) res=max(res,f[i][m]);
cout<<res<<endl;
return 0;
}
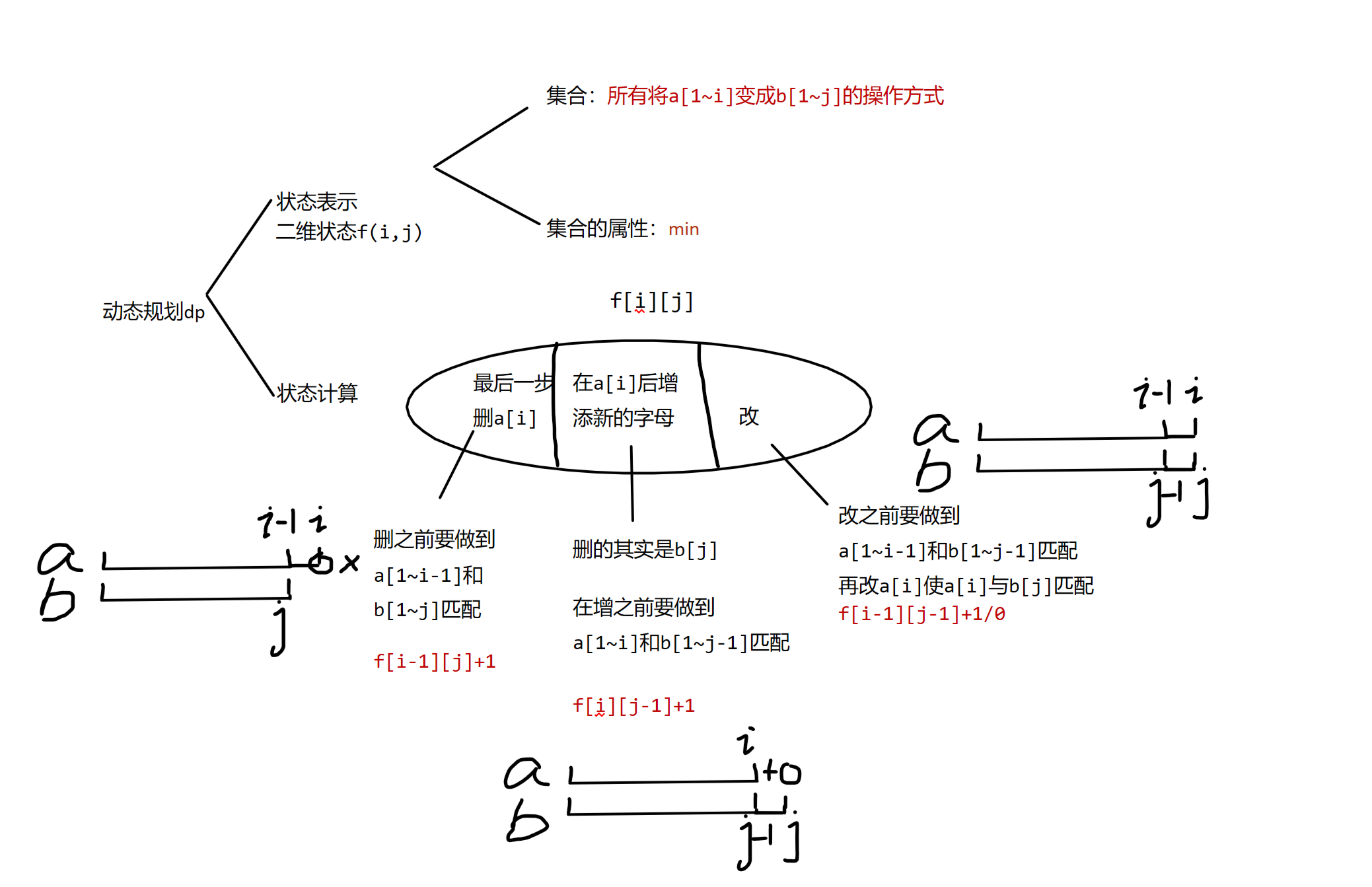
最短编辑距离
给定两个字符串 A 和 B,现在要将 A 经过若干操作变为 B,可进行的操作有:
1.删除–将字符串 A 中的某个字符删除。
2.插入–在字符串 A 的某个位置插入某个字符。
3.替换–将字符串 A 中的某个字符替换为另一个字符。
现在请你求出,将 A 变为 B 至少需要进行多少次操作。
输入格式
第一行包含整数 n,表示字符串 A 的长度。
第二行包含一个长度为 n 的字符串 A。
第三行包含整数 m,表示字符串 B 的长度。
第四行包含一个长度为 m 的字符串 B。
字符串中均只包含大小写字母。
输出格式
输出一个整数,表示最少操作次数。
数据范围
1≤n,m≤1000
输入样例:
10
AGTCTGACGC
11
AGTAAGTAGGC
输出样例:
4
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
char a[N] , b[N];
int n , m ;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cin>>m;
for(int j=1;j<=m;j++) cin>>b[j];
for(int i=0;i<=m;i++) f[0][i]=i;//第一种情况:如果a没有字母就要添加i个,需要i步
for(int i=0;i<=n;i++) f[i][0]=i;//第二种情况:如果b没有字母就要删掉i个,需要i步
//第三种情况,字母从第二个开始
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
f[i][j]=min(f[i-1][j]+1,f[i][j-1]+1);
if(a[i]==b[j]) f[i][j]=min(f[i][j],f[i-1][j-1]);
else f[i][j]=min(f[i][j],f[i-1][j-1]+1);
}
cout<<f[n][m]<<endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号