二分

二分思路

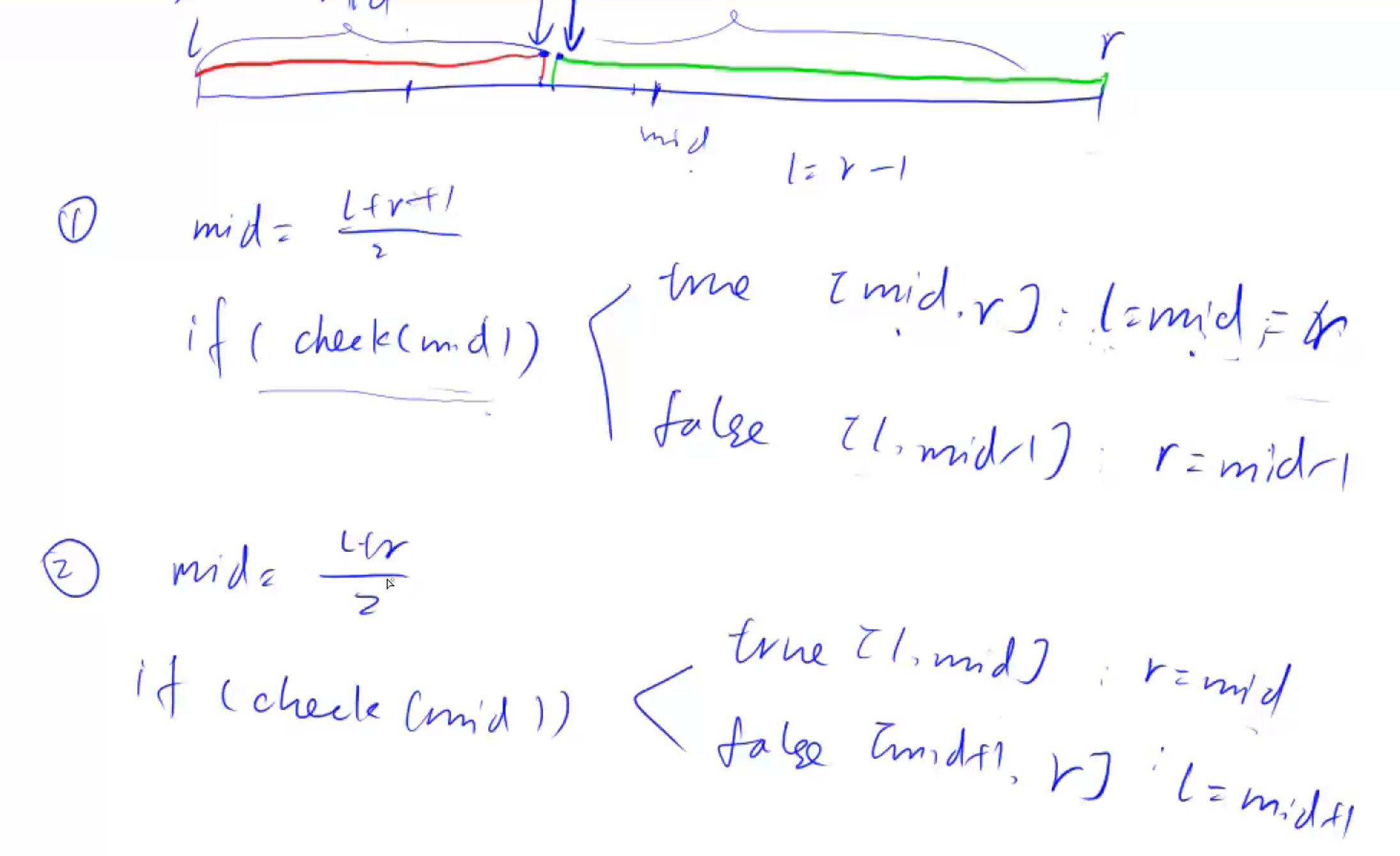
二分模板

整数二分

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1; //此处必须要+1，如果不+1那么当l=r-1时，mid向下取整结果为l，下一行if(ture)则l=mid=l ，将构成死循环
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

浮点数二分

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

分巧克力

儿童节那天有 K 位小朋友到小明家做客。
小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力，其中第 i 块是 Hi×Wi 的方格组成的长方形。
为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足：
形状是正方形，边长是整数，大小相同
例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式

第一行包含两个整数 N 和 K。
以下 N 行每行包含两个整数 Hi 和 Wi。
输入保证每位小朋友至少能获得一块 1×1 的巧克力。

输出格式

输出切出的正方形巧克力最大可能的边长。

数据范围

1≤N,K≤105,
1≤Hi,Wi≤105

输入样例：

2 10
6 5
5 6

输出样例：

2

思路

小巧克力边长 a 一定在 1 – 100000 之间
答案即为：在 1 – 100000 之间找到一个最大的数，使得所有的 (w[i]/a) * (h[i]/a) 之和大于 k。
使用二分法找到 a 的最大取值即为答案。

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
int n , m ;
const int N = 1e5+10;
int h[N],w[N];

bool check(int mid)
{
    ll res=0;//记录分成长度为 mid 的巧克力数量
    for(int i=0;i<n;i++) 
    {
        res+=(ll)(w[i]/mid)*(h[i]/mid);//每一大块可以分成的边长为 mid 的巧克力数量
        if(res>=m) return true;
    }
    return false;
}
int main ()
{
    cin>>n>>m;
    for(int i=0;i<n;i++) cin>>h[i]>>w[i];
    
    int l=1,r=1e5;//小巧克力数量边长一定在 1 -- 100000 之间
    while(l<r)
    {
        int mid = (l+r+1)>>1;
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    cout<<r<<endl;
    return 0;
}

我在哪？

农夫约翰出门沿着马路散步，但是他现在发现自己可能迷路了！
沿路有一排共 N 个农场。不幸的是农场并没有编号，这使得约翰难以分辨他在这条路上所处的位置。
然而，每个农场都沿路设有一个彩色的邮箱，所以约翰希望能够通过查看最近的几个邮箱的颜色来唯一确定他所在的位置。
每个邮箱的颜色用 A..Z 之间的一个字母来指定，所以沿着道路的 N 个邮箱的序列可以用一个长为 N 的由字母 A..Z 组成的字符串来表示。某些邮箱可能会有相同的颜色。
约翰想要知道最小的 K 的值，使得他查看任意连续 K 个邮箱序列，他都可以唯一确定这一序列在道路上的位置。

例如，假设沿路的邮箱序列为 ABCDABC 。
约翰不能令 K=3，因为如果他看到了 ABC，则沿路有两个这一连续颜色序列可能所在的位置。
最小可行的 K 的值为 K=4，因为如果他查看任意连续 4 个邮箱，那么可得到的连续颜色序列可以唯一确定他在道路上的位置。

输入格式

输入的第一行包含 N，
第二行包含一个由 N 个字符组成的字符串，每个字符均在 A..Z 之内。

输出格式

输出一行，包含一个整数，为可以解决农夫约翰的问题的最小 K 值。

数据范围

1≤N≤100

输入样例：

7
ABCDABC

输出样例：

4

代码

#include <bits/stdc++.h>

using namespace std;
int n;
string str;

bool check(int x)
{
    unordered_set<string> st;
    for(int i=0;i+x-1<n;i++)
    {
        string s = str.substr(i,x);
        if(st.count(s)) return false;
        st.insert(s);
    }
    return true;
}
int main()
{
    cin>>n>>str;
    
    int l=1,r=n;
    while(l<r)
    {
        int mid = (l+r)>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    cout<<r<<endl;
    return 0;
}