ODT 学习笔记

本文同步发表于博客园。有问题请不吝指出。

upd on 25/10/30：改的更加有条理了一些，加了模板代码。

前言

这下不得不学 ODT 了……

本文仅介绍 map 实现的 ODT，感觉大家都用 set 来实现，但是用 map 来实现的显然比 set 更加好写啊……

简介

名称：ODT （Old Driver Tree）。也叫珂朵莉树（Chtholly Tree），也被叫做是颜色段均摊，由某毒瘤巨佬在 CF896C 中引入。

特点：ODT 是一种暴力数据结构，和 dsu on tree、势能线段树什么的都比较类似，是类似暴力的优化。其在随机数据下比较高效。但如果询问次数不多的话，在非随机数据下也是 \(O(q \log n)\) 的。

核心思想：将值（颜色）相同的一段区间合并为一个元素。

使用场景：

区间赋值，区间查询——可以使用 map 维护相同颜色段以及段信息。

引入

先看个题，然后从中来学习 ODT：P1840。

这个题显然有其他方法来做，因为它是一个黄题，不过这里就将 ODT 的做法。

题意：在一条数轴上有 \(n\) 个点，分别是 \(1,2,\ldots,n\)。一开始所有的点都被染成黑色。接着我们进行 \(m\) 次操作，第 \(i\) 次操作将 \([l_i,r_i]\) 这些点染成白色。请输出每个操作执行后剩余黑色点的个数。

显然，注意到每次染色后数轴上的点都是黑白相间的。

原本最朴素的暴力是不能通过的，所以我们考虑利用上面的颜色段的性质来对暴力进行优化，也就是减少一些暴力。

假设我们现在要对数轴的红色区间里面进行操作：

（由于作者太懒就使用 s 老师的图了）

我们的朴素暴力显然就是在这个区间里面暴力修改。但是实际上并不用这样——我们要开始优化暴力了。

由于颜色是成段的，所以我们发现，对于每一个段，只需要修改这个段的信息即可。于是，就引出了我们的主角——颜色段均摊。

存储颜色段

set 的写法就直接来存储左右端点和权值，但是 map 不一样。

我们可以简单地使用 \((l,w)\) 来表示颜色段信息，\(l\) 为左端点，\(w\) 为值（注意这里的值和颜色不是一个东西，一个颜色段的权值可以维护很多类型的东西）。

例如：

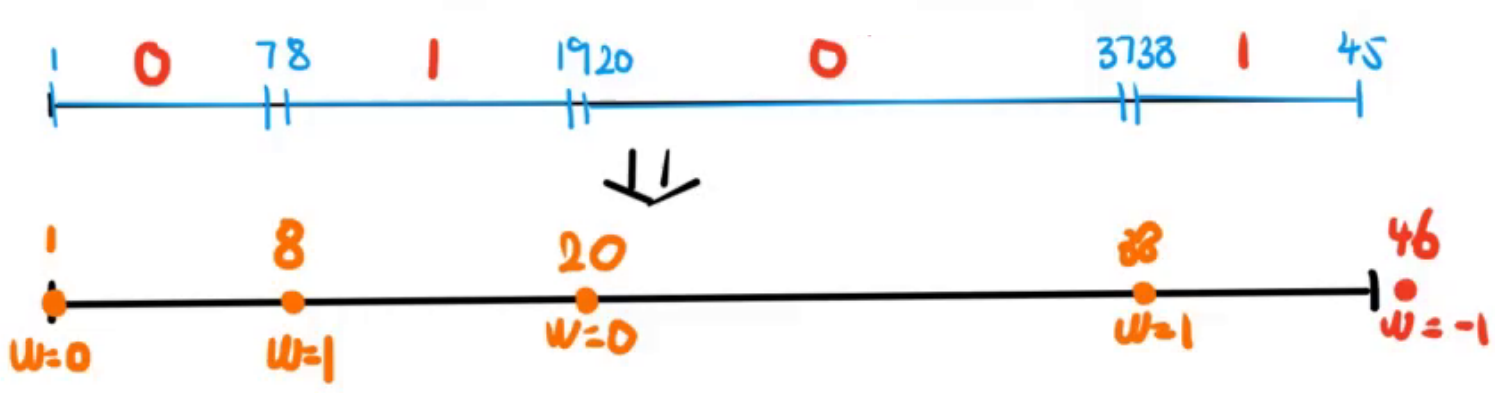
因为数轴上每一个点要么是黑要么是白（也就是说，颜色段之间是没有间隙的），所以这两个表示方式是可以互化的。即如果应用第二个表示方式，我们照样也可以轻松求出区间的右端点。

注意，这里的最右边还有一个值为 \(-1\) 的东西。这个是为了防止边界溢出，因为左边的 \((38,1)\) 颜色段如果不加以限制的话，我们的算法很有可能把它当作是向右无限延长的。而 \(-1\) 只是为了区分其和普通结点而已。

那么这个东西 \((l,w)\) 该如何记录呢？有一个简单好写的方式就是直接使用 map 来维护。

修改

那么我们该怎么应对修改呢？

例如这样：

对区间中的所有数都变成 \(0\)。

在操作后，显然区间中的都变成 \(0\) 了，这会导致中间成为一个连续段。而 \([8,19],[38,45]\) 中只有一部分被波及，所以我们不得不修改一下某些颜色段的信息。

简单模拟一下，大概就能想出来如何应对修改了。

第一步：先把新的颜色段插入进去。

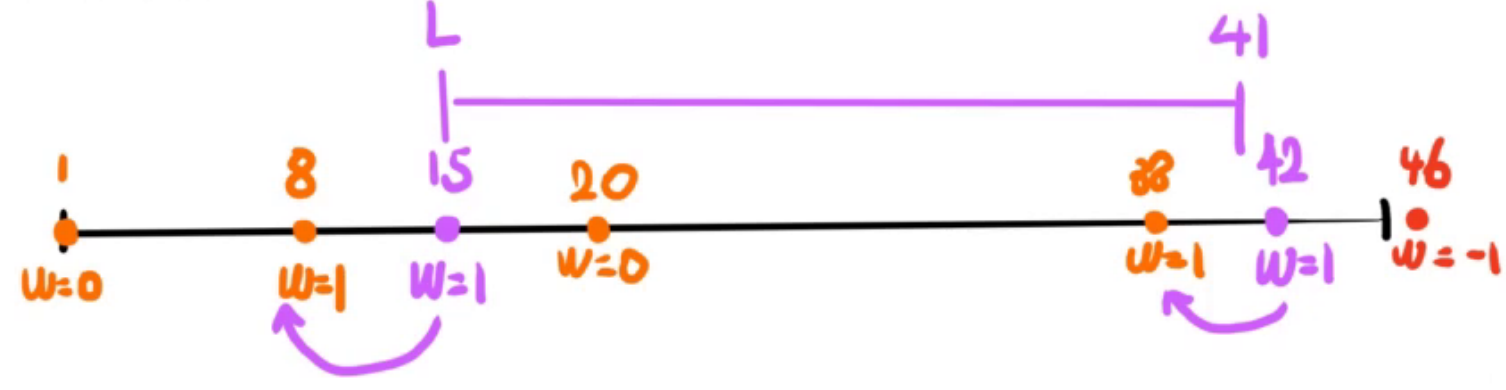
也就是直接二分 \(L,R\) 即可。

第二步：再把中间的颜色段删掉。

这个好像真没办法优化。暴力删除。

第三步：把新的颜色段的权值修改成我们想要的值。

就是直接改。

这样，我们的修改就完成了。

考虑分析一下修改的复杂度。答案是 \(O(q \log n)\)，\(q\) 为询问个数。为什么呢？

因为，每次操作最多会生成两个结点，然后这些生成的结点也只会被删除一次并在后续访问一次。

而二分和修改 map 都是 \(O(\log n)\)，所以最终就是 \(O(q \log n)\)。

这意味着，在任何的数据下（可以不是随机数据！），不带查询的 ODT 的速度都极快。这就是暴力数据结构的厉害之处！！

回到 P1840，这个题剩下的就不多了。对于查询黑色点的总数量，每次修改时都动态维护其即可。

简单总结

根据上文对修改和存储的分析，我们可以发现：ODT 实际上真的没啥东西，本质上，就是使用 set/map 来维护颜色段的区间信息，然后其修改和查询就都是在上面做暴力得出的。

个人感觉，暴力数据结构没有改变其朴素、“野蛮”的本质，但是却对各方面效率有了极大的提升。这也许就是暴力数据结构的最大妙处吧。

查询

有修改但没有查询的就是好的 ODT，那是不是意味着有查询的就是不好的 ODT 呢？

容易想到查询的方法。

查询就是再往数组里面塞查询区间的左右两个端点，然后把里面的所有颜色段的权值加起来即可。（注意这里的加是广义的，也就是说可以不是两个数加起来，还可以是两个二元组加起来，类似合并）

这个复杂度有点高。但是好像也确实是我们目前可以想到的最好的暴力方法。

这个东西单次复杂度就已经达到了 \(O(\min(q,n) \log n)\) 的级别。好像随便精心构造一下数据都能卡掉……

现在我们发现，如果 ODT 没有查询，那它每次就是 \(\log\) 的，还是一个不错的算法，还算优美，还可以解决很多问题。

但是一碰到多次查询，它就会原地爆炸了……

——等等？我们前面说的能把 ODT 的区间查询卡掉的前提情况，是出题人精心构造了数据。那么~~出题人不用脑子造数据~~，或者是数据随机的情况呢？

如果数据是随机的，而且你使用了 map/set 来实现，那么区间查询的理论值是 \(O(q \log \log n)\) 的。

我不会证，只能给个链接跑路了。

代码实现

实现采用 map 的实现。这样子的 ODT 的 split 操作非常的简洁。

代码实现参考了 oi-wiki。

首先介绍一下我们需要的函数：

split：ODT 的核心，分裂区间。 用处是，把一个区间 \([l,r]\) 分裂成 \([l,x-1]\) 和 \([x,r]\) 两个区间。
assign：区间赋值。 即，把 \([l,r]\) 这个区间赋值为 \(v\)。
perform：提取区间来进行操作。 即，把 \([l,r]\) 提取出来进行操作（使用这个操作就可以实现区间加！） / 查询。

`split` 函数

因为 map 有着只存储左端点的优秀方式，所以我们这个时候根本就不需要管 \(l,r\) 的值是多少，把 \(x\) 插进去就可以了。

这也是 map 实现比 set 实现好写很多的主要原因。

void split(int x){
	mp[x]=prev(mp.upper_bound(x))->second;
	//如果 x 这个点不在 map 里面，则这个可以找到最大左端点小于等于 x 的区间
	//如果 x 在，则这个执行过后相当于没有执行。 
}

`assign` 函数

直接三步走即可。

void assign(int l,int r,int val){
	split(r+1),split(l);//第一步：插入结点。注意这里是插入 r+1 
	for(auto it=mp.find(l);it->first<=r;it=mp.erase(it));//第二步：删除区间里面的结点。
	mp[l]=val;//第三步：修改成我们想要的值。 
}

`perform` 函数

感觉和 assign 差不多。

int perform(int l,int r){//这里以区间查询为例，但是 perform 还可以支持其他的区间修改等操作 
	split(r+1),split(l);//一样的，插入要查询 / 修改的结点。可以发现，这不会对时间复杂度有很大影响，最多只会增加常数
	int ans=0;
	for(auto it=mp.find(l);it->first<=r;it=next(it))
		//区间查询 
	return ans; 
}

整体代码

struct ODT{
	map<int,int> mp;
	void init(int x){
		mp.clear();
		mp[1]=/*一开始要赋的初始值*/;
		mp[x+1]=0;//为了防止越界的“墙” ，初值可以随便取，不要混淆就可以了 
	}
	void split(int x){
		mp[x]=prev(mp.upper_bound(x))->second;
		//如果 x 这个点不在 map 里面，则这个可以找到最大左端点小于等于 x 的区间
		//如果 x 在，则这个执行过后相当于没有执行。 
	}
	void assign(int l,int r,int val){
		split(r+1),split(l);//第一步：插入结点。注意这里是插入 r+1 
		for(auto it=mp.find(l);it->first<=r;it=mp.erase(it));//第二步：删除区间里面的结点。
		mp[l]=val;//第三步：修改成我们想要的值。 
	}
	int perform(int l,int r){//这里以区间查询为例，但是 perform 还可以支持其他的区间修改等操作 
		split(r+1),split(l);
		int ans=0;
		for(auto it=mp.find(l);it->first<=r;it=next(it))
			//区间查询 
		return ans; 
	}
};

注意事项

注意到我的代码里面写的是 split(r+1),split(l) 而非 split(l),split(r+1)。这是因为泥土笨笨的题解中提到，后一种写法有概率会 RE。

~~我说昨天晚上调 CF1705E 把我调 RE 弄红温了。~~

P2061 [USACO07OPEN] City Horizon S

我们终于能做点题了……

这个题乍一看需要区间 \(\max\)，非常的棘手。导致我自创了一个复杂的方法，写出了一个会 T 的代码。

void perform(int l,int r,int val){
	split(r+1),split(l);
	int lst=0;
	for(auto it=mp.find(l);it->first<=r;){
		if(it->second<val) {
			it->second=val;
			if(lst==it->second) it=mp.erase(it);
			lst=val;
		}else lst=it->second,it++;
	}
}

但是我们简单的一想，其实并不需要这样复杂！

我们不需要在线处理，答案只需要我们在最后算即可。这启示这我们可以离线处理。

注意到，当高楼的高度递增的时候，区间 \(\max\) 等价于区间赋值。

于是就是普通的区间赋值操作啦。

CF1638E Colorful Operations

这个题就不太中规中距，但是也不难。

首先看操作 \(1\)，不难想到 ODT 来维护。但是我们又会发现操作 \(2\) 不能单单靠 ODT 就可以维护，还需要其他的方法。

因为颜色数也只有 \(n\) 个，而且我们只需要支持单点改，所以我们考虑对于一个颜色开一个懒标记 \(tag_i\)，即延迟标记。当操作 \(2\) 的时候就 \(tag_c+x \to tag_c\)。

这样单点查询 \(x\) 的时候，答案就是 \(a_x+tag_{color_x}\)，\(color_x\) 为询问目前的 \(x\) 的颜色，\(a_x\) 为 \(x\) 位置没算上当前的 \(tag_{color_x}\) 的值（但是算上了 \(x\) 以前的颜色则延迟标记）。

那么操作 \(2\) 和询问都解决了。考虑如何处理 \(1\)。

有两个需要考虑的点，假设 \(x \in [l,r]\)，\(x\) 的颜色要改为 \(c\)：

首先，\(x\) 原本的颜色的延迟标记要加给 \(a_x\)。这个是比较显然的，因为 \(x\) 在之后的一段单点查询里面都不会用原本的 \(color_x\) 的 \(tag\) 来回答询问了。所以要加上。
还有一个不容易考虑到的情况：如果仅有上面的步骤的话，\(c\) 在这个操作 \(1\) 之前积攒下来的 \(tag\) 值也会不小心在单点查询的时候加给 \(x\)，这显然是不正确的。怎么补救呢？此时将 \(a_x\) 减去 \(tag_c\) 即可。

对于操作 \(1\) 的时候的一个颜色段，显然里面加上的东西都是相同的。所以直接使用树状数组来维护区间加、单点查即可。

时间复杂度为 \(O(q \log n)\)，读者自证不难。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1000010;
int tag[N];
int n,q;
struct BIT{
	int tr[N];
	void add(int x,int v){
		for(;x<=n;x+=x&-x) tr[x]+=v;
	}
	int qry(int x){
		int ans=0;
		for(;x;x-=x&-x) ans+=tr[x];
		return ans;
	}
	void upd(int l,int r,int v){
		add(l,v),add(r+1,-v);
	}
}bit;
struct ODT{
	map<int,int> mp;
	void init(int x){
		mp[1]=1,mp[x+1]=0;
	}
	void split(int x){
		mp[x]=prev(mp.upper_bound(x))->second;
	}
	int get(int x){
		return prev(mp.upper_bound(x))->second;
	}
	void assign(int l,int r,int val){
		split(r+1),split(l);
		for(auto it=mp.find(l);it->first<=r;it=mp.erase(it))
			bit.upd(it->first,min(next(it)->first-1,n),tag[it->second]-tag[val]);//注意边界
		mp[l]=val;
	}
}odt;
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>q;
	odt.init(1e9);
	while(q--){
		string s;cin>>s;
		if(s[0]=='C'){
			int l,r,c;cin>>l>>r>>c;odt.assign(l,r,c);
		}else if(s[0]=='A'){
			int c,x;cin>>c>>x;tag[c]+=x;
		}else{
			int x;cin>>x;
			cout<<bit.qry(x)+tag[odt.get(x)]<<endl;
		}
	}
	return 0;
}

posted @ 2025-10-29 21:36 wusixuan 阅读(10) 评论(0) 收藏举报

刷新页面返回顶部

wusixuan