莫队算法学习笔记

莫队算法的发明者是一个叫做莫涛的人，所以被称为莫队算法，简称莫队。

英语 Mo's algorithm

使用场景

莫队算法常常被用来处理多次区间询问的问题，离线处理询问（必须满足！！！）。

插叙：离线是一种得到所有询问再进行计算的方法，是很重要的思想。

对于这种“区间询问”的问题，我们现在就已经可以使用好几种方法：甚至还可以维护修改的线段树、树状数组（不过使用场景有限），以及同样可以很快解决问题的 ST 表……

所以，莫队在很多时候可以被其他算法代替。但是莫队也有很多“专利”，就像分块可以解决很多线段树解决不了的问题（虽然就是慢了点）。

树状数组需要可以区间减法，线段树和 ST 表需要可以区间合并，而莫队需要可以进行区间扩张和区间缩短。

题外话：区间扩张和区间缩短你能想到什么？没错，尺取法。

算法思路

我们不妨解决一个问题，从问题中了解算法的大体思路。

问题：询问区间和。（这显然可以使用前缀和进行维护，但是~~我们假装不会这个~~）

法一：纯暴力。枚举区间内所有的数，加起来即可。 时间复杂度 \(O(qn)\)。

不再阐述。

法二：另一种暴力。方法如下。

假设我们现在已经计算出了 \([l_1,r_1]\) 的区间和，而现在又需要计算 \([l_2,r_2]\) 的区间和。

~~出于懒的本性~~，我们考虑在原 \([l_1,r_1]\) 的区间和上~~动一些手脚~~。

直接将 \(l_1\) 移到 \(l_2\)，然后将 \(r_1\) 移到 \(r_2\)，顺便维护一下即可。

复杂度仍然是 \(O(qn)\)，好像没有优化多少。

~~好像比上面的方法还要蠢~~，但是不必灰心，这种“蠢”的方法正是莫队的起源。

我愿称这种方法为 fit 法。感觉 fit 可以很完整又很形象地概括出这种暴力方法。

法三：莫队。对询问进行了顺序调整，然后使用法二的方法处理即可。

先对询问的序列按照左边界的值分成了 \(\sqrt(n)\) 个块长为 \(\sqrt(n)\) 的块（好奇怪）。

然后对询问排序：

第一关键字：按左边界的块号从小到大排序。（啊？）
第二关键字：按右边界从小到大排序。

看起来非常古怪的一个排序，那么这个排序有什么奇效呢？我们来举个例子。

设 \(n=9,q=10\)。

我们有如下查询：\([2,5],[4,5],[5,9],[1,6],[2,3],[7,8],[9,9],[6,7],[2,8],[3,4]\)。

而我们按照块号排序之后变成了 \([2,3],[3,4],[2,5],[1,6],[2,8],[4,6],[6,7],[5,9],[7,8],[9,9]\) 这个样子。

然后我们画一个图，来使用平面直角坐标系来绘出这些区间（左端点变成了横坐标，右端点变成了纵坐标）。

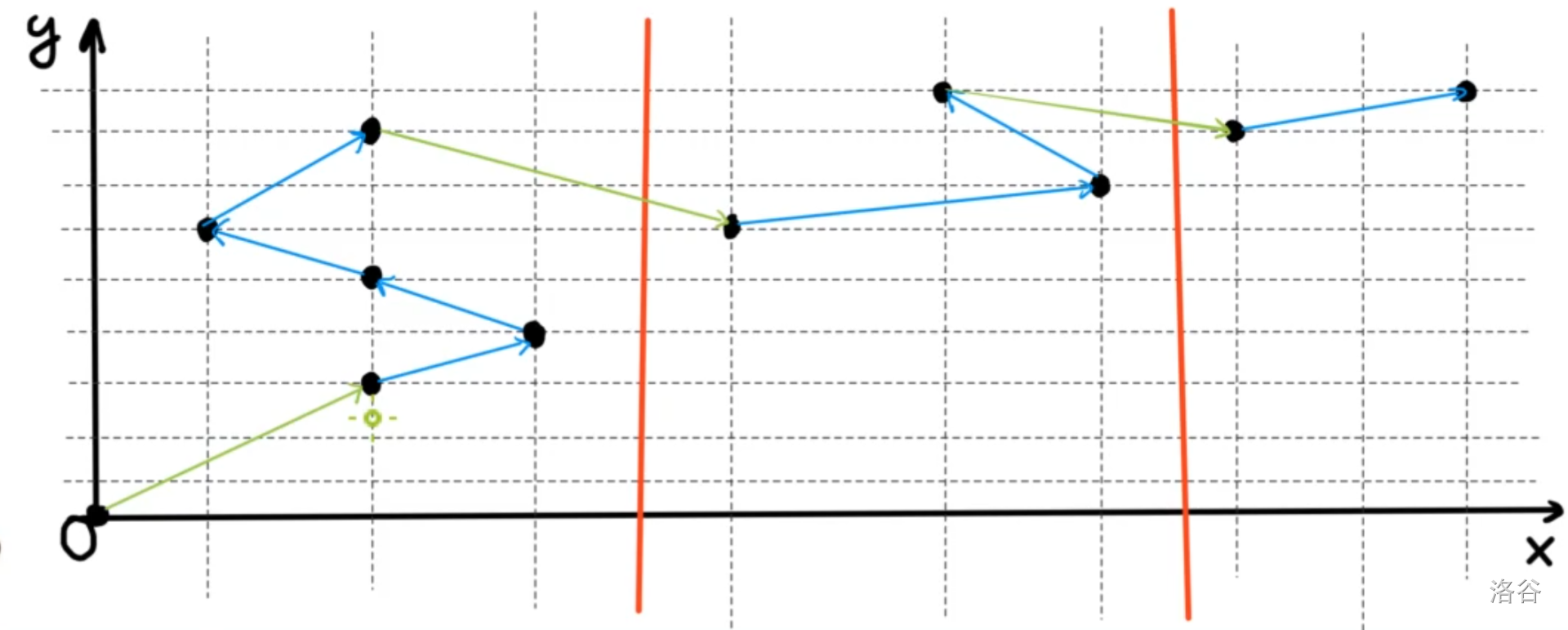
解释一下图片的含义：

为了便于描述，我们先设一开始的区间在 \([0,0]\) 的位置。

因为第一关键字使用块号来排序，所以同一个块内的点一定在一起，已经使用粗的红线分割出三个块（\(\sqrt(9)=3\)）。

我们使用蓝色边来体现块内结点移动，然后使用橙色边来体现块间结点的移动。

容易知道，块的数量是 \(O(\sqrt(n))\) 个，而块的横坐标长度是 \(\sqrt(n)\)（注意，这里的每一个点的横纵坐标均不可能超过 \(n\)，这可是查询）。

因为橙色边的数量和块的数量有关，所以橙色边的数量最多是 \(O(\sqrt(n))\)个，而每一次点之间移动的复杂度不超过 \(n\)（这是区间移动，左端点和右端点总共最多移动 \(n\) 下）。

因此，单算橙色边，时间复杂度为 \(O(n \sqrt(n))\)。

橙色边分析的落脚点在于原区间的移动，考虑使用 抽象之后的点之间的移动 来分析蓝色边的复杂度。

显然，点之间的移动 的次数取决于两点之间的纵坐标和横坐标差。

考虑纵坐标。因为第一关键字在块内中已经失去了作用，而第二关键字保证了我们在块内一定是越爬越高。

而每一个点的横纵坐标均不可能超过 \(n\)，所以单个块内纵坐标总共也只会对时间造成 \(n\) 的影响。

所有的块的纵坐标影响合起来，也只有 \(O(n \sqrt(n))\)，可以接受。

考虑横坐标。根据前文，每一个块的横向长度都不可能超过 \(\sqrt(n)\)，所以横坐标的块内单次只会造成 \(\sqrt(n)\) 的时间影响。

而总共有 \(q\) 个点，相乘起来，是 \(O(q \sqrt(n))\)，仍然可以接受。

经过上面的分析，你现在知道为什么这样排序了吧！

实际上，所有的看起来古怪的算法，都是为了以后恰到好处的运用。

综上所述，莫队的时间复杂度为 \(O((q+n) \sqrt(n))\)。排序是 \(O(n\log n)\) 的，但是相比 \(\sqrt(n)\) 来说还是可以忽略的。

这就是莫队的想法。

模板

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 1000010
int n, q, val[N], ans[N], res, len; //res 为当前区间信息，ans[] 为每一个问题的答案

struct Qry {
	int l, r, id;
} qry[N];//询问

bool cmp(Qry a, Qry b) {
	int ida = (a.l - 1) / len + 1;//计算第一个区间的左边界块号
	int idb = (b.l - 1) / len + 1;//计算第二个区间的左边界块号
	return ida < idb/*第一关键字*/ || (ida == idb && a.r < b.r)/*第二关键字*/;
}

void add(int pos) {
	???//可以自行修改
}//加入对应元素并且重算区间信息。

void del(int pos) {
	???//可以自行修改
}//去除对应元素并且重算区间信息。

void mo() {
	len = sqrt(n);//计算块长
	sort(qry + 1, qry + q + 1, cmp); //对询问排序
	for (int i = 1, l = 1, r = 0; i <= q; ++i) {
		while (l > qry[i].l)
			add(--l);
		while (r < qry[i].r)
			add(++r);
		while (r > qry[i].r)
			del(r--);
		while (l < qry[i].l)
			del(l++);//移动区间
		ans[qry[i].id] = res;
	}
}

实际上，一般的莫队题目的排序部分以及区间移动部分都是一样的，仅仅只有 del 和 add 部分不同。

所以在普通题目的讲解中只考虑 del 和 add 函数的变化。

小优化

一堆 LGM 都无法通过（包括 tourist）的毒瘤莫队题，Code937 用了这个优化就过了。

考虑对移动距离的优化，如果变为下图的话就可以肉眼可见地优化一段移动距离。

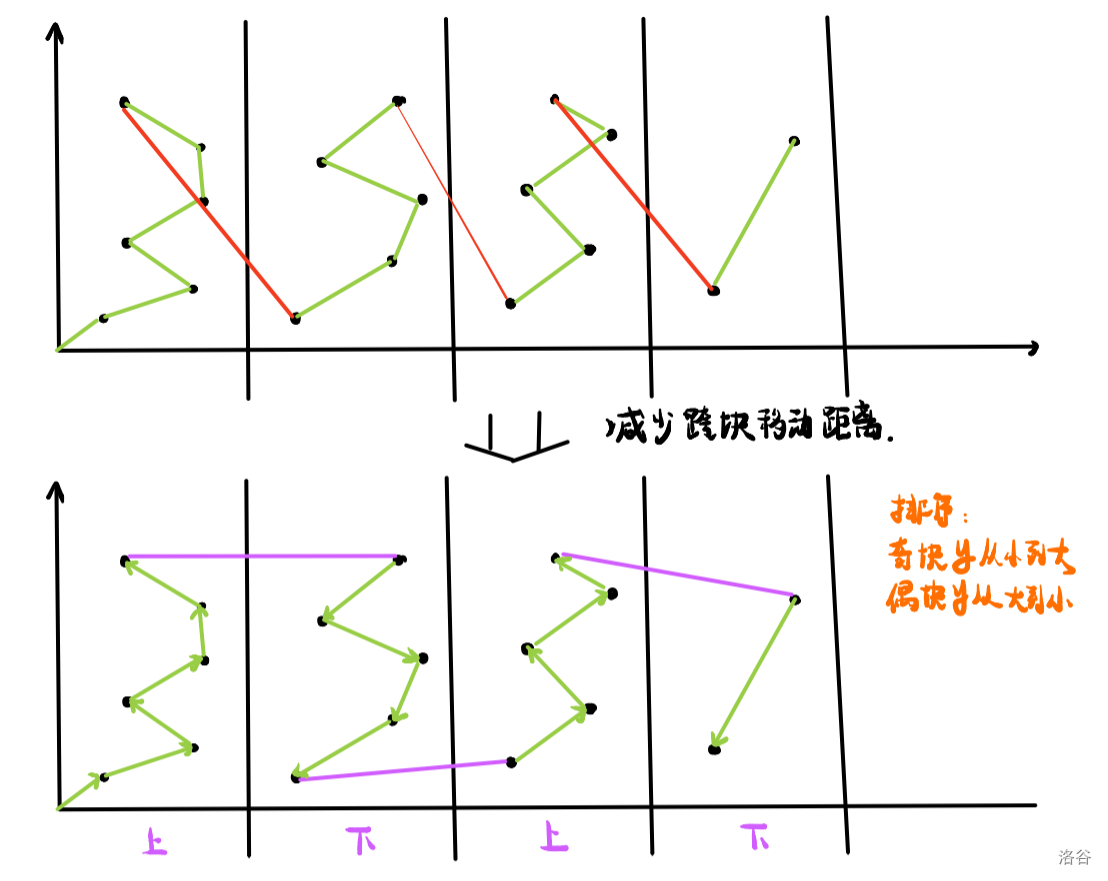
如图，我们只需要按照奇偶性对第二关键字进行排序即可。虽然是常数优化，但是大数据的时候有奇效。

bool cmp(Qry a, Qry b) {
	int ida = (a.l - 1) / len + 1;
	int idb = (b.l - 1) / len + 1;//计算块号
	return ida < idb || (ida == idb && (ida & 1 ? a.r<b.r : a.r>b.r))/*按照奇偶性*/;
}

练习

P3901 数列找不同

~~好家伙一上来就给一道其他 ds 束手无策的题目是吧。~~

注意到值域很小，因此可以直接使用桶来维护每一个值的出现次数，顺便维护当前的区间有没有相同的数。

移动到下一个查询的区间时，直接记录即可。

时间复杂度显然是 \(O(n \sqrt(n))\)。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N];

struct range {
	int l, r, id;
} x[N];
int n, q;
int len;

bool cmp(range a, range b) {
	int ida = (a.l - 1) / len + 1;
	int idb = (b.l - 1) / len + 1;
	return ida < idb || (ida == idb && a.r < b.r);
}
int cnt[N];
int sum = 0;//维护区间存在相同的数的种类

void add(int pos) {
	cnt[a[pos]]++;
	if (cnt[a[pos]] == 2)//如果发现有新的种类
		sum++;
}

void del(int pos) {
	cnt[a[pos]]--;
	if (cnt[a[pos]] == 1)//发现种类已经被剔除
		sum--;
}
int ans[N];

int main() {
	cin >> n >> q;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	len = sqrt(n);
	for (int i = 1; i <= q; i++)
		cin >> x[i].l >> x[i].r, x[i].id = i;
	sort(x + 1, x + q + 1, cmp);
	for (int i = 1, l = 1, r = 0; i <= q; i++) {
		while (l > x[i].l)
			add(--l);
		while (r < x[i].r)
			add(++r);
		while (l < x[i].l)
			del(l++);
		while (r > x[i].r)
			del(r--);//移动
		ans[x[i].id] = sum;
	}
	for (int i = 1; i <= q; i++) {
		if (ans[i])//按照题意，若存在同样种类的数则输出 No
			cout << "No\n";
		else
			cout << "Yes\n";
	}
	return 0;
}

看看这是哪个人写的代码，警钟长鸣~~我不说是谁~~：

AT_abc293_g [ABC293G] Triple Index

发现是区间的很难使用 ds 维护~~除非使用可持久化线段树，但是这已经是省选了~~。

考虑莫队。

发现当加入一个元素的时候，其会与其他在区间中的同样的元素中的任意两个形成三元组。

这句话有点长，我们来拆分一下：设在 \(a_x\) 元素之前区间内已经存在 \(cnt_{a_x}\) 个相同的元素。

则在 \(a_x\) 加入区间之后，会与这 \(cnt_{a_x}\) 个元素中的任意两个元素形成三元组，则会新增 \(C^2_{cnt_{a_x}}\) 个三元组。

当减少一个元素的时候同理，不过 \(cnt++\) 操作要与答案变化操作完全调换。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200010;
int a[N];
int n, q, len;
int cnt[N];

struct range {
	int l, r, id;
} x[N];

bool cmp(range x, range y) {
	int ida = (x.l - 1) / len + 1;
	int idb = (y.l - 1) / len + 1;
	return ida < idb || (ida == idb && x.r < y.r);
}
int ans = 0;

void add(int pos) {
	ans += cnt[a[pos]] * (cnt[a[pos]] - 1) / 2;//计算组合数
	cnt[a[pos]]++;//元素个数改变
}

void del(int pos) {
	cnt[a[pos]]--;//先要改变
	ans -= cnt[a[pos]] * (cnt[a[pos]] - 1) / 2;//减去组合数
}
int sum[N];

signed main() {
	cin >> n >> q;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	for (int i = 1; i <= q; i++) {
		cin >> x[i].l >> x[i].r;
		x[i].id = i;
	}
	len = sqrt(n);
	sort(x + 1, x + q + 1, cmp);
	for (int i = 1, l = 1, r = 0; i <= q; i++) {
		while (l > x[i].l)
			add(--l);
		while (r < x[i].r)
			add(++r);
		while (r > x[i].r)
			del(r--);
		while (l < x[i].l)
			del(l++);
		sum[x[i].id] = ans;
	}
	for (int i = 1; i <= q; i++)
		cout << sum[i] << endl;
	return 0;
}

P3674 小清新人渣的本愿

闲话：我最不喜欢那些往题目中放无关东西的出题人，支持大家用 F12 把它删掉。

考虑莫队。

先来一个比较有启发式的暴力：可以使用三个桶，记录加、减、乘所可以得到的数。每一次加入一个数就尝试将已有的数和它通过加、减、乘凑出一些数。很可惜这样的复杂度是 \(O(n^{\frac{5}{2}})\) 的。

然后考虑优化：可否记录区间内的数是否出现。然后不在每一次区间扩张或区间缩小的时候顺带维护，而是在区间被凑出来的时候直接查询。（即当 x[i].l == l && x[i].r == r 成立的时候看一下能否通过其对应的操作拼凑出来）

每一次可以枚举所有的数，复杂度 \(O(n^2)\)。

然后我们观察到一个很不容易观察到的一个点：发现维护的数组是 bool 的数据类型。

然后考虑 bitset 维护数组中有没有出现这个值。设这个 bitset 为 \(f\)。

发现 bitset 又可以维护加！左移即可！

即对于每一次需要计算差的 \(x\)，直接调用 (f & (f << x)).count()。

那么怎么维护差呢？

不妨将 \(a + b = x\) 变为 \(a = x - b\)。

不妨用一个 bitset \(g_i\) 维护 \(f_{100000-i}\) 的值。

最终对于每一次需要计算和的 \(x\)，直接调用 （(g >> (100000 - x)) & f).count() 即可。

但是乘法怎么办？我们可以不使用 bitset 直接枚举因数，看一下数组中有没有这个因数即可（特别地，如果这个因数恰好是平方根，则要求至少出现两次）。

发现 \(\frac{10^{10}}{w}\) 可以满足需求！！！因为 \(w=64\)！

于是这道题就做完了。

#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 100010;
int a[N];
int ans[N];

struct que {
	int op, l, r, x, id;
} x[N];
int len;

bool cmp(que a, que b) {
	int ida = (a.l - 1) / len + 1;
	int idb = (b.l - 1) / len + 1;
	if (ida == idb)
		return a.r < b.r;
	else
		return ida < idb;
}
bitset<N> f, g;
int cnt[N];

void add(int x) {
	cnt[a[x]]++;
	if (cnt[a[x]] == 1)
		f[a[x]] = g[100000 - a[x]] = 1;
}

void del(int x) {
	cnt[a[x]]--;
	if (cnt[a[x]] == 0)
		f[a[x]] = g[100000 - a[x]] = 0;
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	len = sqrt(n);
	for (int i = 1; i <= m; i++)
		cin >> x[i].op >> x[i].l >> x[i].r >> x[i].x, x[i].id = i;
	sort(x + 1, x + m + 1, cmp);
	for (int i = 1, l = 1, r = 0; i <= m; i++) {
		while (l > x[i].l)
			add(--l);
		while (r < x[i].r)
			add(++r);
		while (r > x[i].r)
			del(r--);
		while (l < x[i].l)
			del(l++);
		if (x[i].op == 1) {
			if ((f & (f << x[i].x)).count())
				ans[x[i].id] = 1;
		} else if (x[i].op == 2) {
			if ((f & (g >> (100000 - x[i].x))).count())
				ans[x[i].id] = 1;
		} else {
			for (int j = 1; j * j <= x[i].x; j++) {
				if (x[i].x % j)
					continue;
				if (f[j] && f[x[i].x / j])
					ans[x[i].id] = 1;
			}
		}
	}
	for (int i = 1; i <= m; i++) {
		if (ans[i])
			cout << "hana\n";
		else
			cout << "bi\n";
	}
	return 0;
}

带修莫队（单点修改）

带修 = 带修改。

修改一般都是单点修改，考区间修改的都是毒瘤，而且很难写。

区间修改的等以后遇到了再来写吧。

使用场景还是和莫队差不多：支持区间扩张，区间收缩，还有单点修改。

然后我们会惊奇地发现，如果按照普通莫队地排序方式对区间查询排序的话，可能不是正确的。

因为可能（假设）询问 \(1\) 是在第 \(1\) 和第 \(2\) 次操作之间，而询问 \(2\) 在第 \(3\) 和第 \(4\) 次操作之间，那么这两个询问所基于的场景就不是相同的，查询的结果也不一定相同。

所以，每一个询问我们还要记录一个时间戳，代表是哪两个相邻的操作之间。

于是，一次区间操作包含以下内容：\((l_i,r_i,t_i)\)，分别为左右端点和时间戳。

考虑再次仿照普通莫队的方式进行推导。

fit 法。

设我们已经得出了询问 \((l_1,r_1,t_1)\) 的值，不妨我们下一个需要求的是 \((l_2,r_2,t_2)\) 询问的值。

首先我们可以通过普通莫队的方法从 \((l_1,r_1,t_1)\) 移动至 \((l_2,r_2,t_1)\)，使得与下一个询问只有时间戳不尽相同。复杂度 \(O(n)\)。

然后我们可以通过推进或回溯的方式将 \(t_1\) 变成 \(t_2\)，就可以得到询问的值。复杂度 \(O(q)\)。

于是可以得到这种方法处理单次询问的复杂度为 \(O(n+q)\)，\(q\) 次查询合起来就是 \(O(q(n+q))\)。不可以接受。

带修莫队。

回想一下，普通莫队是怎么排序的？想不起来了就可以去看前文。

发现带修莫队的区间只不过是从两个值变到了三个值，不妨使用和普通莫队相似的排序方法。

普通莫队是将前 \(2-1\) 个值按照块号排序，则不妨在带修莫队的时候将前 \(3-1\) 个值按照块号排序。

普通莫队是将最后一个值从小到大排序，则不妨在带修莫队的时候将最后一个值也从小到大排序。

于是可以总结出带修莫队下区间的排序方式：

以左边界的块号为第一关键字，从小到大。
以右边界的块号为第二关键字，从小到大。
以时间戳的大小为第三关键字，从小到大。

时间复杂度

带修莫队的时间复杂度很玄学，很难推导所以这里省略具体过程，直接报答案。

重点：设 \(n\) 为左边界的可能规模，\(m\) 为右边界的可能规模，\(q\) 为操作（查询+询问）的次数，则当块长取 \(\frac{n^{\frac{2}{3}} \times q^{\frac{1}{3}}}{m^{\frac{1}{3}}}\) 时，带修莫队取到 \(O(n^{\frac{2}{3}}m^{\frac{2}{3}}q^{\frac{1}{3}})\) 的最优复杂度。

因为大部分时候 \(n\) 和 \(m\) 几乎相同，而 \(q\) 与 \(n\) 同阶，所以最优块长大致为 \(n^{\frac{1}{3}}\times q^{\frac{1}{3}} \approx n^{\frac{2}{3}}\)，此时的最优复杂度取到 \(O(n^\frac{5}{3})\)。

没错，就是这么玄学。但是和普通莫队的时间复杂度差不多，因为 \(\frac{5}{3} \approx \frac{3}{2}\)。这也是很令人惊奇的一个点。

实现

请告诉我如何实现？

实际上，带修莫队主要与普通莫队的最大区别就是版本时间戳的变化维护。但是为了不漏下某些东西，还是将所有板子都贴上来吧。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
int n, q, len;//数据规模，操作数量和块长
int val[N], tmp[N];//一个是当前值，一个是：tmp[id] 代表第 id 次修改替换掉的值（用于还原。）
int res, ans[N];//当前的答案以及所有询问的答案
int tot, p[N], c[N], cnt;//查询

struct Qry {//查询结构
	int l, r, t, id;
} qry[N];

bool cmp(Qry a, Qry b) {
	int ida1 = (a.l - 1) / len + 1, idb1 = (b.l - 1) / len + 1;
	int ida2 = (a.r - 1) / len + 1, idb2 = (b.r - 1) / len + 1;//算出前两个元素的块号
	if (ida1 != idb1)
		return ida1 < idb1;
	else if (ida2 != idb2)
		return ida2 < idb2;
	else
		return a.t < b.t;//比较
}

void add(int pos) {
	???
}

void del(int pos) {
	???
}//类似普通莫队的区间扩张和修改

void addt(int l, int r, int id) {
	if (p[id] < l || r < p[id])
		tmp[id] = val[p[id]], val[p[id]] = c[id];
	//如果修改的位置在区间外：1.记录修改前的值；2.修改当前值。
	else
		del(p[id]), tmp[id] = val[p[id]], val[p[id]] = c[id], add(p[id]);
	//如果修改的位置在区间内：1.删除对应的项；2.记录修改前的值；3.修改当前值；4.加入修改后的项。
}

void delt(int l, int r, int id) {
	if (p[id] < l || r < p[id])
		val[p[id]] = tmp[id];
	//如果修改的位置在区间外：1.直接还原到上一次的取值。
	else
		del(p[id]), val[p[id]] = tmp[id], add(p[id]);
	//如果修改的位置在区间内：1.删除对应的项；2.直接还原到上一次的取值；3.加入还原后的项。
}

void mo() {
	len = pow(n, 2.0 / 3);//注意这里有一些块长的小改动。
	sort(qry + 1, qry + cnt + 1, cmp);
	for (int i = 1, l = 1, r = 0, t = 0; i <= q; ++i) {
		while (l > qry[i].l)
			add(--l);
		while (r < qry[i].r)
			add(++r);
		while (r > qry[i].r)
			del(r--);
		while (l < qry[i].l)
			del(l++);
		while (t < qry[i].t)
			addt(l, r, ++t);
		while (t > qry[i].t)
			delt(l, r, t--);//注意是先移动区间，再移动版本
		ans[qry[i].id] = res;
	}
}

signed main() {
	cin >> n >> q;
	for (int i = 1; i <= n; ++i)
		cin >> val[i];
	for (int i = 1; i <= q; ++i) {
		int op;
		cin >> op;
		if (op == 'R')
			cin >> p[++tot] >> c[tot];
		else
			cin >> qry[++cnt].l >> qry[cnt].r, qry[cnt].id = cnt, qry[cnt].t = tot;
	}
	mo();
	for (int i = 1; i <= cnt; ++i)
		cout << ans[i] << endl;
	return 0;
}

addt() 和 delt() 函数的架构比较复杂，需要牢记其中的维护流程。

带修莫队对于冲击 CSP-S 高分的选手不需要完全掌握（如果考了，也是放在 T4 的位置），对于省选选手需要掌握。

如果您是 CSP-J 的选手，您目前大概不需要这种算法。

回滚莫队

这更是待修的了。

毒瘤 Code937 叫我们自己写板子，回滚莫队滚不动了/kk。拼尽全力终于滚动了两道题。

有时候莫队的增加 or 删除操作很快，但是删除 or 增加（对应关系）操作很慢。这时候，我们就需要考虑不要删除 or 增加，这种思想就是回滚莫队的思想。

请不要认为回滚莫队离自己很远，例如求最大值。加入的时候很开心地 \(O(1)\) 处理，删除的时候就很尴尬：这个值没了，我怎么知道剩下的值的最大值。

~~别告诉我你用 ST 表维护，丢一道题你就不会这么想了：历史的研究~~。

下面开始进入正题：回滚莫队。

回滚莫队的应用场景：多次区间询问（没有询问干嘛要用莫队），区间扩张 or 收缩，区间不收缩 or 不扩张（对应关系），而且，最重要的一点，扩张必须要可以还原。

不删除莫队思路

注意，不删除莫队是指只增加不删除元素的莫队，也就是以回滚代替了删除！

首先要按询问排序，这次和普通莫队也相同。

首先，以左边界所在块号为第一关键字，从小到大。

然后，以右边界为第二关键字，从小到大。

第二步，需要按左边界所属的块，成块处理询问。

此处，需要分类讨论：

Sit1（situation1）.对于左右边界在同一个块。

因为同一个块的长度最多有 \(\sqrt n\)，所以区间的长度 \(\le \sqrt n\)。

而莫队的期望复杂度就是 \(O(q \sqrt n)\)，衍生出来的算法不会比这个复杂度更快。

而区间最多为 \(q\) 个，所以这里暴力是完全没有问题的。

当然，你这里的单次暴力，复杂度应该是线性级别，要不然回滚莫队的复杂度就不正确了。

Sit2（situation2）.对于左边界在一个块，而右边界在另一个块。

给一张图就明白这里的流程了。

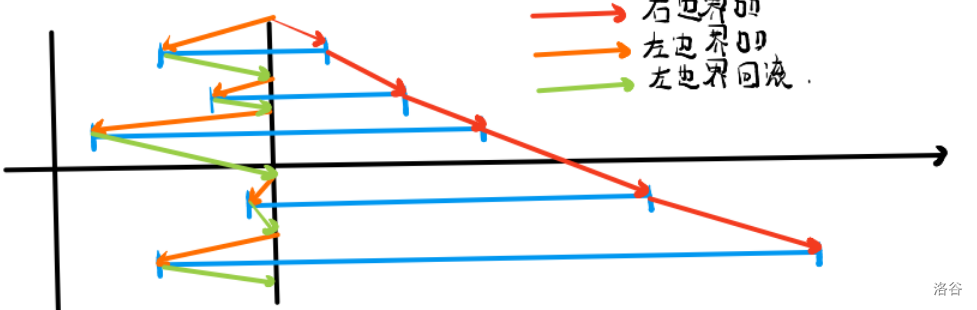
现在知道为什么第二关键字和普通莫队也相同了吧！

设目前的区间的长度为 \(0\)，即将目前的左边界移动到块的右边界的更右边恰好一个位置，即块的右边界 \(+1\)，而右边界恰好移动到块的右边界。

首先需要初始化。

每一次，先将左边界移到目标区间的左边界，然后将右边界移动到目标区间的右边界。

沿路更新答案。到达目标区间后直接更新即可。

然后，就是整个算法最精彩的环节，只有一句话：

将左边界瞬移到块的右边界 \(+1\) 的位置，即初始位置。

就是这么干净利落，直接赋值，直接回滚。然后撤销以 \(l\) 弄出的所有影响。

看不懂思路的可以看模板。

\(\text {Talk is cheap,show me the code!}\)

不删除莫队模板

自己写的模板，可能有亿点丑。将就看看吧。

模板题：AT_joisc2014_c 歴史の研究，就是针对这道题写的模板，贴上去直接过。不支持超代码。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100010;

struct que {
	int l, r, id;
} q[N];//询问
int n, m, len;
int a[N], c[N];
int lft[N], rit[N], pos[N];//块左，块右，点的块号

bool cmp(que a, que b) {
	if (pos[a.l] == pos[b.l])
		return a.r < b.r;
	return a.l < b.l;
}
//---
//下面是自行修改区，更上面的不变（帮助记忆）
int cnt[N], x[N];
int ans[N];//询问
int nw = 0;

int brute(int l, int r) {//暴力，自行修改
	int ret = 0;
	for (int i = l; i <= r; i++)
		x[a[i]]++;
	for (int i = l; i <= r; i++)
		ret = max(ret, x[a[i]] * c[a[i]]);
	for (int i = l; i <= r; i++)
		x[a[i]]--;
	return ret;
}

void add(int x) {//添加，自行修改
	cnt[a[x]]++;
	nw = max(nw, cnt[a[x]] * c[a[x]]);
}

//上面是自行修改区
//---
signed main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	for (int i = 1; i <= m; i++)
		cin >> q[i].l >> q[i].r, q[i].id = i;
	for (int i = 1; i <= n; i++)
		c[i] = a[i];
	sort(c + 1, c + n + 1);
	int tot = unique(c + 1, c + n + 1) - c - 1;
	for (int i = 1; i <= n; i++)
		a[i] = lower_bound(c + 1, c + tot + 1, a[i]) - c;
	//---
	len = sqrt(n);
	for (int i = 1; i <= len; i++)
		lft[i] = rit[i - 1] + 1, rit[i] = i * len;
	if (rit[len] < n)
		len++, lft[len] = rit[len - 1] + 1, rit[len] = n;
	for (int i = 1; i <= len; i++)
		for (int j = lft[i]; j <= rit[i]; j++)
			pos[j] = i;//不知道为啥写这么多可以直接替换掉的东西，可能是因为我记忆力不行？
	sort(q + 1, q + m + 1, cmp);
	//---
	//下面自行修改
	for (int i = 1, l, r, mq = 1; i <= len; i++) {
		for (int j = 1; j <= tot; j++)
			cnt[j] = 0;//首先初始化
		r = rit[i], nw = 0;
        //mq 是目前循环到的询问，nw存储目前的答案。
		while (pos[q[mq].l] == i) {
			l = rit[i] + 1;
			if (q[mq].r - q[mq].l < len) {
				ans[q[mq].id] = brute(q[mq].l, q[mq].r);//在同一个块里面，直接暴力
				mq++;
				continue;
			}
			while (r < q[mq].r)
				add(++r);
			int bef = nw;//记录
			while (l > q[mq].l)
				add(--l);
			ans[q[mq].id] = nw;
			nw = bef;//回溯
			while (l <= rit[i])
				--cnt[a[l++]];//撤销所有的影响
			mq++;
		}
	}
	for (int i = 1; i <= m; i++)
		cout << ans[i] << endl;//输出答案
	return 0;
}

不增加莫队思路

大致思路和不删除莫队一样，有一些小的改变，已经足够简略，需要仔细看。

第一步：输入，对序列分块，将询问按照左端点所属块的编号升序为第一关键字，右端点降序为第二关键字排序

第二步：处理询问，枚举左端点所属的块，将莫队的左端点指针指向当前块左端点的位置，右端点指针指向n。

如果询问的左右端点所属块相同，暴力即可
如果不同，拓展右指针，记录当前状态，再拓展左指针，记录答案
将左指针所造成的改动还原，注意不是删除操作，只是还原为拓展前所记录的状态

不增加莫队代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100010;

struct que {
	int l, r, id;
} q[N];
int n, m, len;
int a[N], c[N];
int lft[N], rit[N], pos[N];//块左，块右，点的块号

bool cmp(que a, que b) {
	if (pos[a.l] == pos[b.l])
		return a.r > b.r;
	return a.l < b.l;
}
//---
//下面是自行修改区
int cnt[N], x[N];
int ans[N];//询问
int nw = 0;

int brute(int l, int r) {???};//暴力，自行修改

void add(int x) {???}//删除，自行修改

//上面是自行修改区
//---
signed main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	for (int i = 1; i <= m; i++)
		cin >> q[i].l >> q[i].r, q[i].id = i;
	for (int i = 1; i <= n; i++)
		c[i] = a[i];
	//到下面的---中间的部分是离散化，视问题而定
	sort(c + 1, c + n + 1);
	int tot = unique(c + 1, c + n + 1) - c - 1;
	for (int i = 1; i <= n; i++)
		a[i] = lower_bound(c + 1, c + tot + 1, a[i]) - c;
	//---
	len = sqrt(n);
	for (int i = 1; i <= len; i++)
		lft[i] = rit[i - 1] + 1, rit[i] = i * len;
	if (rit[len] < n)
		len++, lft[len] = rit[len - 1] + 1, rit[len] = n;
	for (int i = 1; i <= len; i++)
		for (int j = lft[i]; j <= rit[i]; j++)
			pos[j] = i;
	sort(q + 1, q + m + 1, cmp);
	//---
	//下面自行修改
	for (int i = 1, l, r, mq = 1; i <= len; i++) {
		for (int j = 1; j <= tot; j++)
			cnt[j] = 0;//初始化
		r = n, nw = 0;
		while (pos[q[mq].l] == i) {
			l = lft[i];//为左端点
			if (q[mq].r - q[mq].l < len) {
				ans[q[mq].id] = brute(q[mq].l, q[mq].r);
				mq++;
				continue;
			}
			while (r > q[mq].r)//符号方向改变
				add(r--);
			int bef = nw;//记录
			while (l > q[mq].l)//符号方向改变
				add(l++);
			ans[q[mq].id] = nw;
			nw = bef;//回溯
			while (l > lft[i])
				l--, ???; //撤销所有影响
			mq++;
		}
	}
	for (int i = 1; i <= m; i++)
		cout << ans[i] << endl;
	return 0;
}

posted @ 2025-02-22 19:19 wusixuan 阅读(86) 评论(0) 收藏举报

刷新页面返回顶部

wusixuan