NetworkX系列教程(10)-算法之三:关键路径问题

小书匠Graph图论

重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图论中常用算法弄个明白在写这部分.

图论常用算法看我的博客:

下面我将使用NetworkX实现上面的算法,建议不清楚的部分打开两篇博客对照理解.
我将图论的经典问题及常用算法的总结写在下面两篇博客中:
图论---问题篇
图论---算法篇

目录:
* 11.3关键路径算法(CPA)

注意:如果代码出现找不库,请返回第一个教程,把库文件导入.

11.3关键路径算法(CPA)

以下代码从这里复制,由于版本问题,将代码中的:nx.topological_sort(self, reverse=True)改为list(reversed(list(nx.topological_sort(self))))

  1. import networkx as nx 
  2. import matplotlib.pyplot as plt 
  3. from matplotlib.font_manager import *  
  4.  
  5. #定义自定义字体，文件名从1.b查看系统中文字体中来  
  6. myfont = FontProperties(fname='/usr/share/fonts/truetype/wqy/wqy-zenhei.ttc')  
  7. #解决负号'-'显示为方块的问题  
  8. matplotlib.rcParams['axes.unicode_minus']=False  
  9.  
  10. class CPM(nx.DiGraph): 
  11.  
  12. def __init__(self): 
  13. super().__init__() 
  14. self._dirty = True 
  15. self._critical_path_length = -1 
  16. self._criticalPath = None 
  17.  
  18. def add_node(self, *args, **kwargs): 
  19. self._dirty = True 
  20. super().add_node(*args, **kwargs) 
  21.  
  22. def add_nodes_from(self, *args, **kwargs): 
  23. self._dirty = True 
  24. super().add_nodes_from(*args, **kwargs) 
  25.  
  26. def add_edge(self, *args): # , **kwargs): 
  27. self._dirty = True 
  28. super().add_edge(*args) # , **kwargs) 
  29.  
  30. def add_edges_from(self, *args, **kwargs): 
  31. self._dirty = True 
  32. super().add_edges_from(*args, **kwargs) 
  33.  
  34. def remove_node(self, *args, **kwargs): 
  35. self._dirty = True 
  36. super().remove_node(*args, **kwargs) 
  37.  
  38. def remove_nodes_from(self, *args, **kwargs): 
  39. self._dirty = True 
  40. super().remove_nodes_from(*args, **kwargs) 
  41.  
  42. def remove_edge(self, *args): # , **kwargs): 
  43. self._dirty = True 
  44. super().remove_edge(*args) # , **kwargs) 
  45.  
  46. def remove_edges_from(self, *args, **kwargs): 
  47. self._dirty = True 
  48. super().remove_edges_from(*args, **kwargs) 
  49.  
  50. #根据前向拓扑排序算弧的最早发生时间 
  51. def _forward(self): 
  52. for n in nx.topological_sort(self): 
  53. es = max([self.node[j]['EF'] for j in self.predecessors(n)], default=0) 
  54. self.add_node(n, ES=es, EF=es + self.node[n]['duration']) 
  55.  
  56. #根据前向拓扑排序算弧的最迟发生时间 
  57. def _backward(self): 
  58. #for n in nx.topological_sort(self, reverse=True): 
  59. for n in list(reversed(list(nx.topological_sort(self)))): 
  60. lf = min([self.node[j]['LS'] for j in self.successors(n)], default=self._critical_path_length) 
  61. self.add_node(n, LS=lf - self.node[n]['duration'], LF=lf) 
  62.  
  63. #最早发生时间=最迟发生时间,则判断该节点为关键路径上的关键活动 
  64. def _compute_critical_path(self): 
  65. graph = set() 
  66. for n in self: 
  67. if self.node[n]['EF'] == self.node[n]['LF']: 
  68. graph.add(n) 
  69. self._criticalPath = self.subgraph(graph) 
  70.  
  71. @property 
  72. def critical_path_length(self): 
  73. if self._dirty: 
  74. self._update() 
  75. return self._critical_path_length 
  76.  
  77. @property 
  78. def critical_path(self): 
  79. if self._dirty: 
  80. self._update() 
  81. return sorted(self._criticalPath, key=lambda x: self.node[x]['ES']) 
  82.  
  83. def _update(self): 
  84. self._forward() 
  85. self._critical_path_length = max(nx.get_node_attributes(self, 'EF').values()) 
  86. self._backward() 
  87. self._compute_critical_path() 
  88. self._dirty = False 
  89.  
  90. if __name__ == "__main__": 
  91.  
  92. #构建graph 
  93. G = CPM() 
  94. G.add_node('A', duration=5) 
  95. G.add_node('B', duration=2) 
  96. G.add_node('C', duration=4) 
  97. G.add_node('D', duration=4) 
  98. G.add_node('E', duration=3) 
  99. G.add_node('F', duration=7) 
  100. G.add_node('G', duration=4) 
  101.  
  102. G.add_edges_from([ 
  103. ('A', 'B'), 
  104. ('A', 'C'), 
  105. ('C','D'), 
  106. ('C','E'), 
  107. ('C','G'), 
  108. ('B','D'), 
  109. ('D','F'), 
  110. ('E','F'), 
  111. ('G','F'), 
  112. ])  
  113.  
  114. #显示graph 
  115. nx.draw_spring(G,with_labels=True) 
  116. plt.title('AOE网络',fontproperties=myfont) 
  117. plt.axis('on') 
  118. plt.xticks([]) 
  119. plt.yticks([]) 
  120. plt.show() 
  121.  
  122.  
  123. print('关键活动为:') 
  124. print(G.critical_path_length, G.critical_path) 
  125.  
  126. G.add_node('D', duration=2) 
  127. print('\n修改D活动持续时间4为2后的关键活动为:') 
  128. print(G.critical_path_length, G.critical_path) 

关键路径示例(该图非黑色线为手工绘制,数字手工添加)
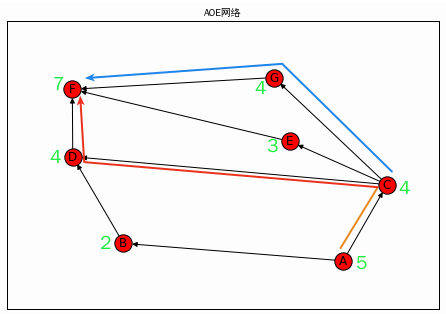
关键路径示例(该图非黑色线为手工绘制,数字手工添加)

从graph中可以知道,有两条关键路径,分别是:A->C->G->F和A->C->D->F,长度都是20.

输出:

关键活动为: 20 ['A', 'C', 'D', 'G', 'F']

修改D活动持续时间4为2后的关键活动为: 20 ['A', 'C', 'G', 'F']

关键活动为: ['A', 'C', 'D', 'G', 'F'],可以构成两条边.D活动持续时间4为2后,关键路径变化.

posted @ 2018-06-28 20:57  好奇不止，探索不息  阅读(2703)  评论(0)    收藏  举报