cf814 D. An overnight dance in discotheque

题意：

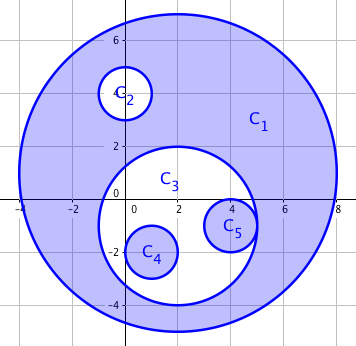
有 n 个圆，他们只能是相互包含，相离或者相切的。

将其分为两组，每组中，只有奇数次覆盖的才会算入面积，求可能的最大面积。

\(n\le 1000\)

思路：

每个圆最多有一个父亲（父亲定义为包含儿子的最小圆），可以有多个儿子。所以所有圆组成一个森林。

森林中，每棵树是独立的。现在要把每棵树的点分成两个集合构造两棵新的树，在新的树中深度为奇的点符号为正，偶数层的点为负

注意到每个圆的面积都大于它的所有后代的面积，首先所有第一层肯定是正的，我们令所有（原树中）第二层也是正的，这样的答案就是最大的。即先把第一层放进第一组，所有（原树中）第二层放进第二组。剩下每个点的正负是确定的。

建图过程是 n^2 的，据说可以用很高级的东西优化到 nlogn

const signed N = 1e3 + 3;
int n, dep[N];
struct node {
    int x, y, r;
} a[N];

bool inside(node &a, node &b) { //a in b
    return pow2(a.x-b.x) + pow2(a.y-b.y) < pow2(a.r+b.r);
}

signed main() {
    iofast;
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y >> a[i].r;

    sort(a + 1, a + 1 + n, [](node &a, node &b) {
         return a.r > b.r;
    });
    for(int i = 1; i <= n; i++)
        for(int j = i + 1; j <= n; j++) //计算深度
            if(inside(a[j], a[i])) dep[j] = dep[i] + 1;

    db ans = 0; for(int i = 1; i <= n; i++)
        ans += pow2(a[i].r) * (!dep[i] || dep[i]%2 ? 1 : -1);
    cout << fixed << setprecision(10) << PI * ans;
}