3 离散信道及其信道容量

目录

• 1 信道的数学模型及分类
  • 1.1 信道分类
    • 1.1.1 用户量分类
    • 1.1.2 信道输入输出关联
    • 1.1.3 信道参数统计特性
    • 1.1.4 信号统计特性
  • 1.2 信道的数学模型
    • 1.2.1 基本模型
    • 1.2.2 根据条件概率分类
  • 1.3 单符号离散信道的数学模型
    • 1.3.1 建模
    • 1.3.2 简单的单符号离散信道模型
• 2 互信息
  • 2.1 信道疑义度
  • 2.2 平均互信息
    • 2.2.1 相关定义
    • 2.2.2 非负性
    • 2.2.3 极值性
    • 2.2.4 交互性/对称性
    • 2.2.5 凸状性
  • 2.3 平均条件互信息
• 3 信道容量及其计算方法
  • 3.1 信道容量
  • 3.2 离散无噪信道的信道容量
    • 3.2.1 无噪无损信道
    • 3.2.2 无损信道
    • 3.2.3 无噪有损信道
  • 3.3 对称离散信道的信道容量
  • 3.4 准对称信道的信道容量
  • 3.5 一般离散信道的信道容量
  • 3.6 离散无记忆扩展信道的信道容量
• 4 信源与信道的匹配
  • 4.1 信道剩余度
• 5 例题
  • 5.1 一般离散无记忆信道的信道容量的计算
  • 5.2 准对称信道的信道容量的计算

1 信道的数学模型及分类

1.1 信道分类

1.1.1 用户量分类

1. 两端信道：单用户
2. 多段信道：多用户

1.1.2 信道输入输出关联

1. 无反馈信道：输出对输入无影响、无作用
2. 反馈信道：输出对输出有影响、起作用

1.1.3 信道参数统计特性

1. 固定参数信道：信道参数的统计特性不随时间的变化而改变——时不变
2. 时变参数信道：信道参数的统计特性随时间的变化而改变——时变

1.1.4 信号统计特性

1. 离散信道：输入序列和输出序列取值都是离散的，也称为数字信道
2. 连续信道：输入序列和输出序列取值都是连续的
3. 半离散信道/半连续信道：输出序列与输出序列的取值不同，一个是离散的，另一个是连续的
4. 波形信道：信道的输出输出都是模拟信号，又称模拟信道
   以下内容首先研究的是无反馈、固定参数的单用户离散信道

1.2 信道的数学模型

1.2.1 基本模型

信道的数学模型一般如图所示：

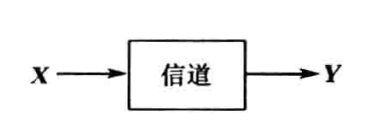
其中输入信号 \(X\) 与输出信号 \(Y\) 均为矢量，且输入信号 \(X=(X_{1},X_{2},\dots,X_{i},\dots,X_{N})\)，输出信号 \(Y=(Y_{1},Y_{2},\dots,Y_{i},\dots,Y_{N})\)，其中 \(i=1,2,\dots,N\) 表示 \(N\) 个不同时刻；而每个随机变量 \(X_{i}\) 与 \(Y_{i}\) 分别取自符号集 \(A=\{ a_{1},a_{2},\dots,a_{r} \}\) 和 \(B=\{ b_{1},b_{2},\dots,b_{s} \}(r不一定等于s)\)。另外，信道中存在条件概率 \(P(y|x)\) 描述了输入信号与输出信号的统计依赖关系，反映了信道的统计特性
另外，离散信道也可用 \([X,P(y|x),Y]\) 来描述

1.2.2 根据条件概率分类

1 无干扰(无噪声)信道
当信道中的噪声很小时 (几乎忽略不计)，信道的输入信号与输出信号存在确定的对应关系，即：

\[\begin{gather*} y=f(x) \\ p(y|x)= \begin{cases} 1 & y=f(x) \\ 0 & y\neq f(x) \end{cases} \end{gather*} \]

2 有干扰无记忆信道
信道中存在干扰，则输入符号与输出符号之间并没有确定的对应关系；无记忆信道强调符号与符号之间不存在依赖关系。故满足离散无记忆信道的充要条件是：

\[P(y|x)=P(y_{1}y_{2}\dots y_{N}|x_{1}x_{2}\dots x_{N})=\prod_{i=1}^N P(y_{i}|x_{i}) \]

3 有记忆有干扰信道
信道中存在干扰，且符号之间存在依赖关系
处理该信道的最直观的方式为将记忆较强的 \(N\) 个符号当作一个矢量符号来处理，这时候再认为各矢量符号之间是无记忆的，但这样处理会存在误差
另外，也可以将其看作马尔可夫链的形式进行处理，但是处理起来较为麻烦，只有在较为简单的情况下才能得到比较简单的结果

1.3 单符号离散信道的数学模型

1.3.1 建模

以下模型的前提为：离散无记忆信道
单符号离散信道强调了单符号与离散的条件，根据这两个条件，我们可以进行如下建模：
设单符号离散信道的输入变量为 \(X\)，取值为 \(X=\{ a_{1},a_{2},\dots,a_{r} \}\)；输出变量为 \(Y\)，取值为 \(Y=\{ b_{1},b_{2},..,b_{s} \}\)，且此时的条件概率为：

\[P(y|x)=P(y=b_{j}|x=a_{i})=P(b_{j}|a_{i}) \]

这一组条件概率称为信道的传递概率或转移概率
即使信道中存在噪声，但是输出符号依然是 \(b_{1},b_{2},\dots b_{s}\) 中的一个，所以我们可以知道：

\[\sum_{j=1}^s P(b_{j}|a_{i})=1 \]

1.3.2 简单的单符号离散信道模型

• 二元对称信道 (BSC)
  该信道是一种特殊信道，不妨假设其输入符号 \(X\) 取值为 \(\{ 0, 1 \}\)，输出符号 \(Y\) 取值为 \(\{ 0,1 \}\)，此时 \(r=s=2\)，不妨令 \(a_{1}=b_{1}=0\)，\(a_{2}=b_{2}=1\)，又有传递概率为：

\[\begin{gather*} P(b_{1}|a_{1})=P(0|0)=1-p=\overline{p} \\ P(b_{2}|a_{2})=P(1|1)=1-p=\overline{p} \\ P(b_{1}|a_{2})=P(0|1)=p \\ P(b_{2}|a_{1})=P(1|0)=p \end{gather*} \]

且 \(0\leq p \leq 1\)，另外，我们可以用如下矩阵来描述该信道：

\[\begin{gather*} 0 \qquad 1 \\ \begin{aligned} 0 \\ 1 \end{aligned} \begin{bmatrix} 1-p & p \\ p & 1-p \end{bmatrix} \end{gather*} \]

• 二元删除信道 (BEC)

  二元删除信道的输入符号数量 \(r=2\)，输出符号 \(s=3\)，输入符号 \(X\in \{ 0, 1 \}\)，输出符号 \(Y\in \{ 0,2,1 \}\)，传递矩阵为：

\[\begin{gather*} 0 \qquad 2 \qquad 1 \\ \begin{aligned} 0 \\ 1 \end{aligned} \begin{bmatrix} p & 1-p & 0 \\ 0 & 1-p & p \end{bmatrix} \end{gather*} \]

该信道的现实意义是一个存在干扰的信道，其在高电平与低电平时会出现波动，可能无法一直监测判定为 \(1\) 或 \(0\)，故此时我们会设定高电平门限与低电平门限，而中间态的信号我们则判定其为符号 \(2\)

由此可知，一般的离散单符号信道的传递概率矩阵如下，其横向为输出符号 \(b_{1},b_{2},\dots,b_{s}\)，纵向为输入符号 \(a_{1},a_{2},\dots,a_{r}\)：

\[\begin{bmatrix} P(b_{1}|a_{1}) & P(b_{2}|a_{1}) & \dots & P(b_{s}|a_{1}) \\ P(b_{1}|a_{2}) & P(b_{2}|a_{2}) & \dots & P(b_{s}|a_{2}) \\ \dots \\ P(b_{1}|a_{r}) & P(b_{2}|a_{r}) & \dots & P(b_{s}|a_{r}) \\ \end{bmatrix} \]

其中有：

\[0\leq P(b_{j}|a_{i})\leq 1 \ and \ \sum_{j=1}^s P(b_{j}|a_{i})=1 \]

对于该信道，有输入符号与输出符号的联合概率为 \(P(x=a_{i},y=b_{j})=P(a_{i}\ b_{j})\)，则有：

\[P(a_{i}\ b_{j})=P(a_{i})P(b_{j}|a_{i})=P(b_{j})P(a_{i}|b_{j}) \]

显然 \(P(b_{j}|a_{i})\) 为发出 \(a_{i}\) 接收 \(b_{j}\) 的概率，为先验概率/先向概率；而 \(P(a_{i}|b_{j})\) 为接收 \(b_{j}\) 但发出 \(a_{i}\) 的概率，为后验概率/后向概率
而根据联合概率，有 \(P(b_{j})=\sum_{i=1}^r P(a_{i})P(b_{j}|a_{i})\)，矩阵形式为：

\[\begin{bmatrix} P(b_{1}) \\ P(b_{2}) \\ \dots \\ P(b_{s}) \end{bmatrix} = \mathbf{P}^T \begin{bmatrix} P(a_{1}) \\ P(a_{2}) \\ \dots \\ P(a_{r}) \end{bmatrix} \quad (r\neq s) \]

由后验概率得到：

\[\sum_{i=1}^r P(a_{i}|b_{j})=1 \]

2 互信息

2.1 信道疑义度

信道输入信源 \(X\) 的熵 \(H(X)\) 为：

\[H(X)=\sum_{i=1}^r P(a_{i})\log \frac{1}{P(a_{i})}=-\sum_{X}P(x)\log P(x) \]

显然，该信源熵的计算是根据先验概率计算而来，故又称为先验熵，而对于后验概率 \(P(x|b_{j})\)，有：

\[H(X|b_{j})=\sum_{i=1}^r P(a_{i}|b_{j})\log \frac{1}{P(a_{i}|b_{j})}=-\sum_{X}P(x|b_{j})\log P(x|b_{j}) \]

称后验概率所计算出的熵为后验熵，对该后验熵求期望，得到：

\[\begin{aligned} H(X|Y)=E[H(X|b_{j})]&=\sum_{j=1}^s P(b_{j})H(X|b_{j})=\sum_{i=1}^r \sum_{j=1}^s P(b_{j})P(a_{i}|b_{j})\log \frac{1}{P(a_{i}|b_{j})} \\ &=\sum_{i=1}^r \sum_{j=1}^s P(a_{i}\ b_{j})\log \frac{1}{P(a_{i}|b_{_{j}})}=\sum_{XY} P(xy)\log \frac{1}{P(x|y)} \end{aligned} \]

对于条件熵 \(H(X|Y)\)，我们称其为信道疑义度，表明了当输出端接收到输出符号 \(Y\) 后，对于输入端的变量 \(X\) 尚存在的平均不确定性，一般的，\(H(X|Y)<H(X)\)

2.2 平均互信息

2.2.1 相关定义

根据前述内容，我们可以知道在接收到符号 \(X\) 之前与接收到符号 \(X\) 之后时的不确定度存在差异，已知前验熵 \(H(X)\) 与后验熵 \(H(X|Y)\) 之间的关系一般为：\(H(X|Y)<H(X)\)
一般的，我们把在接收到符号 \(X\) 之前的平均不确定性 \(H(X)\) 与接收到 \(X\) 之后的平均不确定性 \(H(X|Y)\) 之间的差异 \(H(X)-H(X|Y)\) 称为 \(X\) 与 \(Y\) 之间的平均互信息 \(I(X;Y)\)：

\[I(X;Y)=H(X)-H(X|Y) \]

其表明了接收到输出符号后平均每个符号的获得的信息量 (消除的不确定性)，也反映了两个随机变量之间的约束程度
对于互信息 \(I(x;y)\)，有

\[I(x;y)=\log \frac{P(x|y)}{P(x)}=\log \frac{P(xy)}{P(x)P(y)}=\log \frac{P(y|x)}{P(y)} \]

对于平均互信息 \(I(X;Y)\)，有

\[I(X;Y)=\sum_{X,Y} P(xy) \log \frac{P(y|x)}{P(y)} \]

proof:

\[\begin{aligned} I(X;Y)&=\sum_{X} P(x)\log \frac{1}{P(x)}-\sum_{X,Y}P(xy) \log \frac{1}{P(x|y)} \\ &注意到\ \sum_{Y} P(x|y)=1,\ 则\ \sum_{X}P(x)\times 1=\sum_{X}P(x)\sum_{Y}P(x|y) \\ &=\sum_{X,Y} P(x)P(x|y)=\sum_{X,Y}P(xy) \\ 原式\ &=\sum_{X,Y} P(xy)\log \frac{1}{P(x)}-\sum_{X,Y}P(xy)\log \frac{1}{P(x|y)} \\ &=\sum_{X,Y}P(xy)\log \frac{P(x|y)}{P(x)}\quad (命题得证) \\ &=\sum_{X,Y}P(xy) \log \frac{P(xy)}{P(x)P(y)} \\ &=\sum_{X,Y}P(xy) \log \frac{P(y|x)}{P(y)} \end{aligned} \]

另外，对于平均互信息和互信息，有如下关系：

\[I(X;Y)=E_{X,Y}[I(x;y)]=\sum_{X,Y} P(xy)I(x;y)=\sum_{X,Y} P(xy)\log \frac{P(x|y)}{p(x)} \]

关于平均互信息与信息熵的关系，已知 \(H(XY)=H(X)+H(X|Y)=H(Y)+H(X|Y)\)，我们有以下推导：

\[\begin{aligned} I(X;Y)&=H(X)-H(X|Y) \\ &=H(X)+H(Y)-H(XY) \\ &=H(Y)-H(Y|X) \end{aligned} \]

具体内容在 2 离散信源及其信息测度 中有具体阐述，借鉴其图如下：

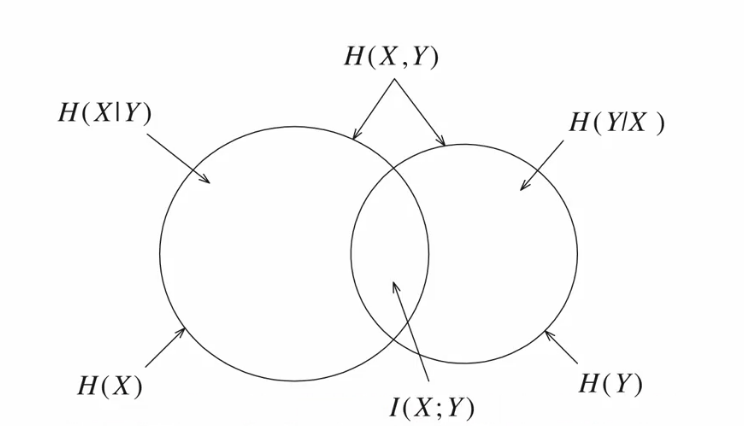
上图具体阐述了平均互信息与相关的熵的关系
其中 \(H(X|Y)\) 为信道疑义度，表明了信源符号通过有噪声信道后所引起的信息量损失，故也可以称为损失熵；而输出端信源 \(Y\) 的熵 \(H(Y)\) 等于接收到关于 \(X\) 的信息量 \(I(X;Y)\) 加上 \(H(Y|X)\)，这是由于信道中的噪声产生的扰动，故也可以称 \(H(Y|X)\) 为噪声熵或散布度

2.2.2 非负性

离散信道输入概率空间为 \(X\)，输出概率空间为 \(Y\)，显然有 \(I(X;Y)\geq 0\)，当 \(X\) 与 \(Y\) 统计独立时，等号成立

2.2.3 极值性

平均互信息 \(I(X;Y)\) 满足：

\[I(X;Y)\leq \min[H(X),H(Y)] \]

已知平均互信息满足

\[\begin{aligned} I(X;Y)&=H(X)-H(X|Y) \\ &=H(X)+H(Y)-H(XY) \\ &=H(Y)-H(Y|X) \end{aligned} \]

显然原式成立

2.2.4 交互性/对称性

因为 \(P(xy)=P(yx)\)，故显然有：

\[I(X;Y)=\sum_{X,Y}P(xy)\log \frac{P(xy)}{P(x)P(y)}=\sum_{X,Y} P(yz)\log \frac{P(yx)}{P(y)P(x)}=I(Y;X) \]

2.2.5 凸状性

平均互信息 \(I(X;Y)\) 是输入信源的概率分布 \(P(x)\) 的 \(\cap\) 型凸函数 (又称上凸函数)
平均互信息 \(I(X;Y)\) 是信道传递概率 \(P(y|x)\) 的 \(\cup\) 型凹函数 (又称下凸函数)

2.3 平均条件互信息

由于在 2 离散信源及其信息测度 有关于平均条件互信息的部分阐述，故以下仅阐述相关概念与定义
互信息 \(I(X;Y)\) 是两个概率空间中两事件之间的互信息，平均互信息 \(I(X;Y)\) 是两个概率空间 \(X\)、\(Y\) 之间的平均互信息，将其推广到三个或多个概率空间中求事件之间互信息时，研究平均条件互信息就有了相关的意义，下面不妨研究三个概率空间中的问题
在已知事件 \(z\in Z\) 的条件下，接收到 \(y\) 后获得关于某事件 \(x\) 的条件互信息为：

\[I(x;y|z)=\log \frac{P(x|yz)}{P(x|z)}=\log \frac{P(y|xz)}{P(y|z)}=\log \frac{P(xy|z)}{p(x|z)P(y|z)} \]

可以发现，平均条件互信息与平均互信息的差别是先验概率与后验概率的某一特定条件下的取值
另外，当已知 \(y\in Y\)，\(z\in Z\) 时，获得的关于 \(x\in X\) 的联合互信息为：

\[\begin{aligned} I(x;yz)&=\log \frac{P(x|yz)}{P(x)}=\log \frac{P(x|y)P(x|yz)}{P(x)P(x|y)} \\ &=\log \frac{P(x|y)}{P(x)}+\log \frac{P(x|yz)}{P(x|y)} \\ &= I(x;y)+I(x;z|y) \end{aligned} \]

同理可得：

\[I(x;yz)=I(x;z)+I(x;y|z) \]

其平均条件互信息 \(I(X;Y|Z)\) (其中 \(\sum_{Y}P(xz|y)=1\)) 为：

\[\begin{aligned} I(X;Y|Z)&=E[I(x;y|z)]=\sum_{X}\sum_{Y}\sum_{Z} P(xyz)\log \frac{P(x|yz)}{P(x|z)} \\ &=\sum_{X}\sum_{Y}\sum_{Z} P(xyz)\left[ \log \frac{1}{P(x|z)}- \log \frac{1}{P(x|yz)} \right] \\ &=\sum_{Y}P(xz|y) \sum_{X}\sum_{Z}P(xz) \log \frac{1}{P(x|z)} - \sum_{X}P(x)\sum_{Y}\sum_{Z} P(x|yz) \log \frac{1}{P(x|yz)} \\ &= \sum_{X}\sum_{Z}P(x)P(x|z) \log \frac{1}{P(x|z)} - \sum_{X}\sum_{Y}\sum_{Z}P(x)P(x|yz) \log \frac{1}{P(x|yz)} \\ &=H(X|Z)-H(X|ZY) \quad (命题得证)\\ &=\sum_{X}\sum_{Y}\sum_{Z} P(xyz)\log \frac{P(xy|z)}{P(x|z)P(y|z)} \\ &=H(X|Z)+H(Y|Z)-H(XY|Z) \end{aligned} \]

另外，平均条件互信息与平均互信息有如下关系：

\[\begin{gather*} I(X;YZ)=E(I(x;yz))=\sum_{X}\sum_{Y}\sum_{Z} P(xyz)\log \frac{P(x|yz)}{P(x)} \\ \begin{aligned} 故\ I(X;YZ)&=I(X;Y)+I(X;Z|Y) \\ &=I(X;Z)+I(X;Y|Z) \end{aligned} \end{gather*} \]

3 信道容量及其计算方法

3.1 信道容量

研究信道的主要目的是讨论平均每个符号所传输的信息量，即信道的信息传输率 \(R\)
显然，信道的信息传输率就是平均互信息，即：

\[R=I(X;Y)=H(X)-H(X|Y)\quad (比特/符号) \]

另外，我们也可以考虑信道在单位时间内所传输的平均信息量，即：

\[R_{t}=\frac{1}{t} I(X;Y)=\frac{1}{t} H(X)-\frac{1}{t} H(X|Y)\quad (比特/秒) \]

我们一般称 \(R_{t}\) 为信息传输速率
根据平均互信息的凸状性，对于平均互信息关于输入随机变量 \(X\) 的概率分布 \(P(x)\)，存在一个最大值 \(\max\{ I(X;Y) \}\)，不妨定义该最大值为信道容量 \(C\)，即

\[C=\mathop{\max}_{P(x)} \{ I(X;Y) \} \quad (比特/符号) \]

而相应的输入概率分布称为最佳输入分布，若平均传输一个符号需要 \(t\) 秒钟，则信道单位时间内平均传输的最大信息量为

\[C_{t}=\frac{1}{t} \mathop{\max}_{P(x)} \{ I(X;Y) \} \quad (比特/秒) \]

其中，二元对称信道的信道容量为 \(C=1-H(p)\)

3.2 离散无噪信道的信道容量

3.2.1 无噪无损信道

无噪无损信道的输入符号与输出符号之间存在一一对应的关系，其信道传输概率为：

\[P(y|x)= \begin{cases} 1\quad y=f(x) \\ 0\quad y\neq f(x) \end{cases} \]

在离散无噪无损信道中，信道疑义度即损失熵 \(H(X|Y)\) 与信道的噪声熵 \(H(Y|X)\) 都为 \(0\)，故该类信道的平均互信息为

\[I(X;Y)=H(X)=H(Y) \]

故此时的信道容量为：

\[C=\mathop{\max}_{P(x)} \{ I(X;Y) \}=\mathop{\max}_{P(x)} [H(X)]=\log r \]

3.2.2 无损信道

若信道的传输矩阵中每一列有一个且仅有一个非零元素时，此信道一定是有噪无损信道
无损信道的损失熵等于 \(0\)，噪声熵大于 \(0\)
所以，无损信道的平均互信息有如下关系：

\[I(X;Y)=H(X)<H(Y) \]

综上，无损信道的信道容量为：

\[C'=\mathop{\max}_{P(x)} H(X)=\log r \quad (比特/符号) \]

当且仅当输入信源为等概率分布时，信道的信息传输概率才能达到极大值

3.2.3 无噪有损信道

该信道的先验概率 \(P(y|x)\) 等于 \(0\) 或 \(1\)，即输出 \(Y\) 是输入 \(X\) 的确定函数，但并非一一对应；因此，后验概率 \(P(x|y)\) 并非为 \(0\) 或 \(1\)
无噪有损信道的噪声熵 \(H(Y|X)\) 为 \(0\)，但信道疑义度 \(H(X|Y)\neq 0\). 虽然此类信道在接收符号后不能完全消除对 \(X\) 的不确定性，信息有所损失，但由于输出端 \(Y\) 的平均不确定性因为无噪而不会增加，故该信道称为无噪有损信道或确定信道
无噪有损信道的平均无信息有如下关系：

\[I(X;Y)=H(Y)<H(X) \]

其信道容量为：

\[C''=\mathop{\max}_{P(x)}H(Y)=\log s \quad (比特/符号) \]

当且仅当输出信源 \(Y\) 为等概率分布时，信道的信息传输概率才能达到极大值，而且一定能找到一个输入分布使得输出分布 \(Y\) 达到等概率分布

3.3 对称离散信道的信道容量

对称离散信道的特点是其信道矩阵具有很强的对称性，其对称性表现为：

• 信道矩阵的每一行都是由同一集的元素的不同排列而成 \(\{ p_{1}',p_{2}',\dots,p_{s}' \}\)，且每一行都是另一行的置换
• 信道矩阵的每一列都是由同一集的元素的不同排列而成 \(\{ q_{1}',q_{2}',\dots,q_{r}' \}\)，且每一行都是另一行的置换
  具有这种特点的信道，我们称为对称离散信道.
  一般情况下，\(r\neq s\)，当 \(r=s\) 时，\(\{ q_{i}' \}\) 集和 \(\{ p_{i}' \}\) 集相同，若 \(r<s\)，则 \(\{ q_{i}' \}\) 集为 \(\{ p_{i}' \}\) 集的子集
  下列信道矩阵为对称离散信道的信道矩阵：

\[P= \begin{bmatrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{6} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} \end{bmatrix} \quad 或 \quad P= \begin{bmatrix} \frac{1}{2} & \frac{1}{3} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{2} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{6} & \frac{1}{2} \end{bmatrix} \]

若输入符号和输出符号个数相同，不妨假设都为 \(r\)，那么信道矩阵为：

\[P= \begin{bmatrix} \overline{p} & \frac{p}{r-1} & \frac{p}{r-1} & \dots & \frac{p}{r-1} \\ \frac{p}{r-1} & \overline{p} & \frac{p}{r-1} & \dots & \frac{p}{r-1} \\ \dots & \dots & \dots & \dots & \dots \\ \frac{p}{r-1} & \frac{p}{r-1} & \frac{p}{r-1} & \dots & \overline{p} \end{bmatrix} \]

式中 \(0\leq p\)，\(\overline{p}\leq 1\)，且 \(p+\overline{p}=1\)，则此信道被称为强对称信道或均匀信道；此类信道中总的错误概率被均匀分给了 \(r-1\) 个输出符号
此时该类信道的平均互信息为

\[I(X;Y)=H(Y)-H(Y|X) \]

已知 \(H(Y|X=x)=\sum_{Y} P(y|x)\log \frac{1}{P(y|x)}=H(p_{1}',p_{2}',\dots,p_{s}')\)，故 \(I(X;Y)\) 为：

\[I(X;Y)=H(Y)-H(p_{1}',p_{2}',\dots,p_{s}') \]

此时的信道容量 \(C\) 为：

\[C=\mathop{\max}_{P(x)} [H(Y)-H(p_{1}',p_{2}',\dots,p_{s}')] \]

一般的，通过推导可以得到当输入符号 \(X\) 等概率分布时，输出符号 \(Y\) 也是等概率分布，此时的对称离散信道的信道容量 \(C\) 为

\[C=\log s-H(p_{1}',p_{2}',\dots,p_{s}') \quad (比特/符号) \]

3.4 准对称信道的信道容量

准对称信道是指可以将信道矩阵 \(\mathbf{P}\) 分成若干个互不相交的子集矩阵 \(B_{k}\)，且满足 \(B_{1}\cap B_{2}\cap\dots \cap B_{n}=\emptyset\)，\(B_{1}\cup B_{2}\cup\dots \cup B_{n}=Y\)，且子集矩阵 \(B_{k}\) 为对称矩阵，此时我们称信道矩阵 \(\mathbf{P}\) 所对应的信道为准对称信道
例如，有如下矩阵

\[\mathbf{P}_{1}= \begin{bmatrix} 0.7 & 0.1 & 0.2 \\ 0.2 & 0.1 & 0.7 \end{bmatrix} \]

我们可以分解为

\[\begin{bmatrix} 0.7 & 0.2 \\ 0.2 & 0.7 \end{bmatrix} \qquad \begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix} \]

此时这两个矩阵满足对称性，我们称 \(\mathbf{P}_{1}\) 为准对称信道的传输矩阵
可以证明，当准对称离散信道的信道容量的输入分布是等概率分布时 (最佳输入分布)，且准对称离散信道容量为：

\[C=\log r-H(p_{1}',p_{2}',\dots,p_{s}')-\sum_{k=1}^n N_{k}\log M_{k} \]

其中 \(r\) 为输入符号集元素个数， \((p_{1}',p_{2}',\dots,p_{s}')\) 为准对称信道的传输矩阵中的行元素；当矩阵被划分为 \(n\) 个不相交的子集时，\(N_{k}\) 是第 \(k\) 个子矩阵 \(\mathbf{Q}_{k}\) 中行元素之和，\(M_{k}\) 是第 \(k\) 个子矩阵 \(\mathbf{Q}_{k}\) 中列元素之和

3.5 一般离散信道的信道容量

从前述相关推导，我们可以知道，信道容量就是在固定信道条件下，对所有可能的输入概率分布 \(P(x)\) 求平均互信息的极大值。我们已知互信息 \(I(X;Y)\) 是输入概率分布 \(P(x)\) 的 \(\cap\) 型凸函数，所以极大值一定存在
另外，由于 \(I(X;Y)\) 是关于 \(r\) 个变量 \(\{ P(a_{1}),P(a_{2}),\dots,P(a_{r}) \}\) 的多元函数，并满足 \(\sum_{i=1}^r P(a_{i})=1\)，所以可以使用拉格朗日乘子法来计算该条件极值
具体推导过程略去，最后得到以下方程组

\[\begin{cases} C=\sum_{j=1}^s P(b_{j}|a_{i}) \log \frac{P(b_{j}|a_{i})}{P(b_{j})}=\lambda+\log e \\ \sum_{i=1}^r P(a_{i})=1 \end{cases} \]

对于上述方程组的第一个公式，不妨将等式两边同时乘以使得 \(I(X;Y)\) 达到极值的概率 \(p_{i}\) 并求和，得到

\[C=\sum_{i=1}^r \sum_{j=1}^s p_{i}P(b_{j}|a_{i})\log \frac{P(b_{j}|a_{i})}{P(b_{j})}=\lambda+\log e \]

即 \(C=\lambda+\log e\)，令 \(I(x_{i};Y)=\sum_{j=1}^s P(b_{j}|a_{i})\log \frac{P(b_{j}|a_{i})}{P(b_{j})}\)，则由方程组的第一项得

\[C=I(x_{i};Y) \]

所以，对于一般离散信道有下述定理：
Theorem 3.1: 一般离散信道的 \(I(X;Y)\) 达到极大值(信道容量)的充要条件是输入概率分布 \(\{ p_i \}\) 满足：

\[\begin{cases} I(x_{i};Y)=C, & 对所有\ x_{i}\ 其\ p_{i}\neq 0 \\ I(x_{i};Y)\leq C, & 对所有\ x_{i}\ 其\ p_{i}=0 \\ \end{cases} \]

从上述定理，我们可以知道当信道平均互信息达到信道容量时，输入信源符号集中每一个信源符号为输出端提供相同的互信息，只有概率为 \(0\) 的符号除外；显然，这符合直觉，已知当概率为 \(0\) 的符号不会被接收端接收，对于接收端而言，所有接收端的符号的概率分布一致，那么此时的平均互信息取到极大值，即为此时的信道容量
值得注意的是，信道的最佳输入分布并不是唯一的，但信道的输出概率分布是唯一的

另外，对于式 \(C=\sum_{j=1}^s P(b_{j}|a_{i}) \log \frac{P(b_{j}|a_{i})}{P(b_{j})}\)，我们可以将其写成如下形式

\[\begin{gather*} C=\sum_{j=1}^s P(b_{j}|a_{i})\log P(b_{j}|a_{i})-\sum_{j=1}^s P(b_{j}|a_{i})\log P(b_{j}) \\ \sum_{j=1}^s P(b_{j}|a_{i})\log P(b_{j}|a_{i})=\sum_{j=1}^s P(b_{j}|a_{i})(C+\log P(b_{j})) \end{gather*} \]

不妨假设 \(\beta_{j}=C+\log P(b_{j})\)，有

\[\sum_{j=1}^s P(b_{j}|a_{i})\log P(b_{j}|a_{i})=\sum P(b_{j}|a_{i})\beta_{j} \]

此时为一个包含有 \(s\) 个未知数 \(\beta_{j}\)，有 \(r\) 个方程的非齐次线性方程组
如果 \(r=s\)，则信道传递矩阵 \(\mathbf{P}\) 为非奇异矩阵，则此方程组有解，并可以求出 \(\beta_{j}\) 的数值，结合 \(\sum_{j=1}^s P(b_{j})\) 的附加条件可以求得信道容量为

\[C=\log_{2}\sum_{j} 2^{\beta_{j}} \]

对应的输出概率分布为

\[P(b_{j})=2^{\beta_{j}-C} \]

再由 \(P(b_{j})=\sum_{i=1}^r P(a_{i})P(b_{j}|a_{i})\) 解出达到信道容量的最佳输入分布

3.6 离散无记忆扩展信道的信道容量

离散无记忆扩展信道为离散无记忆信道的 \(N\) 阶扩展，在 [[2 离散信源及其信息测度]]中已有类似阐述，将信源引申为信道即可。
对于离散无记忆扩展信道，我们有以下定理
Theorem 3.2: 一般离散信道 \([\mathbf{X}, P(\mathbf{y}|\mathbf{x}), \mathbf{Y}]\)，设 \(X=(X_{1}X_{2}\dots X_{N})\)，\(Y=(Y_{1}Y_{2}\dots Y_{N})\)，其中

\[X_{i}\in A=\{ a_{1}, a_{2}, \dots, a_{r} \},Y_{i}\in B=\{ b_{1}, b_{2}, \dots, b_{s} \},\mathbf{x}\in \mathbf{X}, \mathbf{y}\in \mathbf{Y},x_{i}\in X_{i},y_{i}\in Y_{i} \]

则有：

• 当信道是无记忆的，即信道传递概率满足 \(P(y|x)=\prod_{i=1}^N P(y_{j}|x_{i})\)，有

\[I(\mathbf{X}|\mathbf{Y})\leq \sum_{i=1}^N I(X_{i};Y_{i}) \]

• 当信道的输入信源是无记忆的，即满足 \(P(x)=\prod_{i=1}^N P(x_{i})\)，有

\[I(X;Y)\geq \sum_{i=1}^N I(X_{i};Y_{i}) \]

• 当信道和信源都是无记忆的，即同时满足信道传递概率 \(P(y|x)=\prod_{i=1}^N P(y_{j}|x_{i})\) 和 \(P(x)=\prod_{i=1}^N P(x_{i})\)，有

\[I(X;Y)=\sum_{i=1}^N I(X_{i};Y_{i}) \]

对于一般的离散无记忆信道的 \(N\) 次扩展信道，有

\[I(X;Y)\leq \sum_{i=1}^N I(X_{i};Y_{i}) \]

所以其信道容量为

\[C^{N}=\mathop{\max}_{P(x)}I(X;Y)=\mathop{\max}_{P(x)}\sum_{i=1}^N I(X_{i};Y_{i})=\mathop{\max}_{P(x)}\sum_{i=1}^N C_{i} \]

不妨令 \(C_{i}=\mathop{\max}_{P(x)}I(X_{i};Y_{i})\)，显然，在时不变信道中各个符号传输时的信道环境基本一致，则 \(C_{i}=C\)，所以有

\[C^{N}=NC \]

这说明离散无记忆的 \(N\) 次扩展信道的信道容量等于原单符号离散信道的信道容量的 \(N\) 倍，当且仅当输入信源是无记忆的且每一输入变量 \(X_{i}\) 的分布各自达到最佳分布 \(P(x)\) 时，才能达到这个信道容量 \(NC\)
一般情况下，消息序列在离散无记忆的 \(N\) 次扩展信道中传输的信息量 \(I(X;Y)\leq NC\)

4 信源与信道的匹配

4.1 信道剩余度

当信道确定后，信道容量就确定了。对于该信道，只有当输入符号的概率分布满足一定条件 (最佳分布概率) 时才能达到信道容量
即只有特定的信源才能使信道的传输率达到最大值
此时，我们认为当且仅当信息传输率达到信道容量时，我们认为信源与信道达到匹配，否则称信道有剩余
此时我们引入信道剩余度，其定义如下：

\[信道剩余度=C-I(X;Y) \]

其中 \(C\) 是该信道的信道容量，\(I(X;Y)\) 为此时的信源通过该信道实际传输的平均信息量
而信道相对剩余度为：

\[信道相对剩余度=\frac{C-I(X;Y)}{C}=1-\frac{I(X;Y)}{C} \]

在无损信道中，\(C=\log r\)，\(I(X;Y)=H(X)\)，其中 \(H(X)\) 为输入信道的信源熵，故

\[无损信道的相对剩余度=1-\frac{H(X)}{\log r} \]

可以发现，对于无损信道而言，其信道相对剩余度与信源剩余度等价

5 例题

5.1 一般离散无记忆信道的信道容量的计算

设离散无记忆信道输入符号 \(X\) 的符号集为 \(\{ a_{1}, a_{2}, a_{3}, a_{4} \}\)，输出符号 \(Y\) 的符号集为 \(\{ b_{1}, b_{2}, b_{3}, b_{4} \}\)，其信道的传递矩阵如下，求该信道的信道容量

\[\begin{bmatrix} \frac{1}{2} & \frac{1}{4} & 0 & \frac{1}{4} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{2} \end{bmatrix} \]

解：

\[\begin{gather*} 由\ \sum_{j=1}^s P(b_{j}|a_{i})\log P(b_{j}|a_{i})=\sum P(b_{j}|a_{i})\beta_{j}\ 可得：\\ \begin{cases} \frac{1}{2}\beta_{1} + \frac{1}{4}\beta_{2}+\frac{1}{4}\beta_{4} =\frac{1}{2}\log \frac{1}{2}+\frac{1}{4}\log \frac{1}{4} + \frac{1}{4}\log \frac{1}{4} \\ \beta_{2}=0 \\ \beta_{3}=0 \\ \frac{1}{4}\beta_{1}+\frac{1}{4}\beta_{3}+\frac{1}{2}\beta_{4}=\frac{1}{4}\log \frac{1}{4}+\frac{1}{4}\log \frac{1}{4}+\frac{1}{2}\log \frac{1}{2} \end{cases} \\ 解得\ \beta_{1}=\beta_{4}=-2,\beta_{2}=\beta_{3}=0 \\ 信道容量\ C=\log_{2}(2^{-2}+2^{0}+2^{0}+2^{-2})=\log_{2}5-1(bit/符号) \\ 输出概率分布为\ P(b_{1})=P(b_{4})=2^{-2-\log_{2}5+1}=\frac{1}{10},P(b_{2})=P(b_{3})=2^{0-\log_{2}5+1}=\frac{4}{10} \\ 最佳输入概率分布为\ P(a_{1})=P(a_{4})=\frac{4}{30}, P(a_{2})=P(a_{3})=\frac{11}{30} \end{gather*} \]

5.2 准对称信道的信道容量的计算

还没学完，边学边写/(ㄒoㄒ)/~~

1 信息论——基础理论与应用, 傅祖芸