1 信源
1.1 信源的分类
- 离散信源
- 连续信源
1.2 信源模型
1.2.1 平稳信源
一般来说,我们假设信源输出的是平稳的随机序列,也就是说序列的统计性质与时间的推移无关,该信源我们称为平稳信源
1.2.2 离散信源
离散信源其符号集的取值是有限的或可数的,可以用一维离散型随机变量 \(X\) 来描述信源输出
其符号集 \(a_{i}\) 与其先验概率 \(P(a_{i})\) 的关系为:
\[\begin{gather*}
\begin{bmatrix}
X \\
P(x)
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q} \\
P(a_{1}), P(a_{2}), \dots, P(a_{q})
\end{bmatrix} \\
且\ \sum_{i=1}^q P(a_{i}) = 1
\end{gather*}
\]
上述信源中的符号个数为有限个,且每次必定从中选取一个消息输出,满足完备集条件
1.2.3 连续信源
连续信源与离散信源的区别在于,连续信源的符号集是连续的,例如区间 \((a,b)\),或是实数集 \((-\infty,+\infty)\),用一维连续型随机变量 \(X\) 来描述信源:
\[\begin{gather*}
\begin{bmatrix}
X \\
p(x)
\end{bmatrix}
=
\begin{bmatrix}
(a,b) \\
p(x)
\end{bmatrix}
\\
且\ \int_{a}^b p(x)dx=1
\end{gather*}
\]
1.2.4 离散/连续平稳信源
对于随机矢量 \(X\),若每个随机矢量 \(X_{i}\) 可能的取值为有限的/可数的,且随机矢量 \(X\) 的各维概率分布都与时间起点无关 (平稳信源),则称其为离散平稳信源
对于随机矢量 \(X\),若每个随机矢量 \(X_{i}\) 取值为连续的连续型随机变量,且信源为平稳信源,则称其为连续平稳信源
1.2.5 无记忆信源
无记忆信源的本质是信源所发出的所有符号是统计独立的,即信源输出的随机序列 \(X=X_{1}X_{2}\dots X_{N}\) 中,各随机变量 \(X_{i}(i=1,2,\dots,N)\) 之间是无依赖、统计独立的,即每个输出的符号之间没有联系,各自独立。
此时 \(N\) 维随机变量概率分布为:
\[P(X)=P(X_{1}X_{2}\dots X_{N})=P_{1}(X_{1})P_{2}(X_{2})\dots P_{N}(X_{N})
\]
在平稳信源中,其 \(N\) 维随机变量概率分布中每一个符号所输出的概率与时间 (时刻) 无关,故概率 \(P_{i}(X_{i})\) 的角标 \(i\) 可以去除:
\[P(X)=P(X_{1}X_{2}\dots X_{N})=P(X_{1})P(X_{2})\dots P(X_{N})=\prod_{i=1}^N P(X_{i})
\]
若不同时刻的离散随机变量都取自于同一符号集 \(A:\{a_{1},a_{2},\dots ,a_{q}\}\),则:
\[P(x=a_{i})=P(a_{i_{1}})P(a_{i_{2}})\dots P(a_{i_{N}})=\prod_{i_{k}=1}^q P(a_{i_{k}})
\]
以上 \(P(x=a_{i})\) 为所有时刻的视角下符号为 \(a_{i}\) 的概率测度
对于单独的 \(X\) 视角,由信源空间 \([X,P(x)]\) 描述的信源 \(X\) 为离散无记忆信源:
\[\begin{gather*}
\begin{bmatrix}
X \\
P(x)
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q} \\
P(a_{1}), P(a_{2}),\dots, P(a_{q})
\end{bmatrix} \\
且\ \sum_{i=1}^q P(a_{i})=1
\end{gather*}
\]
1.2.6 有记忆信源
若某个符号的出现概率与前一符号的状态有关,则我们可以认为这是一个有记忆信源
当记忆长度为 \(m+1\) 时,称这种有记忆信源为 \(m\) 阶马尔可夫信源,即信源每次发送的符号只与前 \(m\) 个符号有关,而与其他更前面的符号无关。
例如对于 \(m\) 阶马尔可夫信源输出的随机序列为 \(X=X_{1}X_{2}\dots X_{i-1}X_{i}X_{i+1}\dots X_{N}\),在该序列中,\(X_{i}\) 只与前 \(m\) 个符号有关,设各时刻随机变量 \(X_{k}\) 的取值为 \(x_{k}\),\(x_{k}\in X_{k},k=1,2,\dots,i, \dots,N\) ,则描述的各随机变量之间存在依赖关系的条件概率为:
\[P(x_{i}|\dots x_{i+2}x_{i+1}x_{i}x_{i-1}x_{i-2}\dots x_{i-m}\dots x_{1})=P(x_{i}|x_{i-1}x_{i-2}x_{i-3}\dots x_{i-m})
\]
即此时 \(i\) 时刻的符号与从 \(x_{i-m}\) 到 \(x_{i-1}\) 的符号有关,即从 \(x_{i-m}\) 到 \(x_{i-1}\) 的符号为 \(x_{i}\) 时刻的条件,而与其他的符号无关
若上述条件概率与时间无关,即信源输出的符号序列可以看作时齐马尔可夫链,此信源称为时齐马尔可夫信源 (离散)
连续有记忆信源与连续无记忆信源取决于输出符号序列为离散或连续的
2 信息熵
2.1 自信息
一个随机事件 \(X\) 发生的概率为 \(p\),那么他的自信息(信息量)为
\[I=-\log p
\]
自信息的本质是信息的不确定性,或时间 \(X\) 给接收方提供的信息量
如果 \(X\) 为多个随机事件的集合,则信息量为
\[I=-\sum_{x\in X}\log p(x)
\]
上述内容表达的为离散的随机变量的计算方法,如果为连续的随机变量,则 \(P(x)\) 表示为概率密度
从上述公式可以看出,信息与事件出现的概率密切相关.
2.2 信息熵(entropy)
信息熵描述了信源整体的不确定程度,由于自信息 \(I\) 是一个随机变量(事件不唯一),故信息熵用来描述对于自信息的一个数学期望,又称为平均信息量
\[ H(X)=-\sum_{x\in X}p(x) \log p(x)=-E_{X}[\log p(X)]
\]
Remark: 信息的熵仅仅与其分布有关,而与随机变量 X 的取值无关
显然的,我们可以观察到下面这个关系:
\[ H(X)\leq \log|X|
\]
等号成立的条件为 \(X\) 的分布均匀,任意事件的 \(p\) 相等
2.3 条件概率
在事件 \(B\) 已经发生的条件下,事件 \(A\) 发生的概率,称为条件概率 \(P(A|B)\),记作:
\[ P(A|B)=\frac{P(AB)}{P(B)}
\]
当满足下列任一条件时,可以称事件 \(A\) 与事件 \(B\) 独立,反之认为事件 \(A\) 与事件 \(B\) 相关.
\[ P(A|B)=P(A),\qquad P(AB)=P(A)P(B)
\]
2.4 条件熵(Conditional entropy)
条件熵描述的是以某个时间为前提时,随机变量 \(X\) 的不确定度.
\[ H(X|Y=y)=-\sum_{x\in X}p(x|y)\log p(x|y)
\]
显然的,也可以发现:
\[ H(X|Y)\leq H(X)
\]
等号成立的条件为 \(X,\ Y\) 相互独立
对于多个变量的情况,例如三个变量,如果已知 \(p(y)>0\):
\[p(x,y,z)=\frac{p(x, y)p(y,z)}{p(y)}=p(x,y)p(z|y)=p(x)p(y|x)p(z|y)
\]
注意到,\(p(x,y)=p(x)p(y|x)\).
另外,对于条件概率分布的情况,我们有:
\[\begin{aligned}
H(Y|X)&=-\sum_{x\in X,y\in Y} p(x,y)\log p(y|x)=-E[\log p(Y|X)]\\
&=-\sum_{x\in X}p(x)H(Y|X=x)
\end{aligned}
\]
2.5 联合熵(Joint entropy)
联合熵的可以理解为对于 \((X,\ Y)\) 联合信源的不确定度
\[ H(X,Y)=-\sum_{x\in X, y\in Y}p(x, y)\log p(x, y)=-E[\log p(X,Y)]
\]
注意到:
\[ H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)
\]
且根据之前的不等式,我们可以观察得到:
\[ H(X,Y)\leq H(X)+H(Y)
\]
2.6 离散的随机向量的熵
可以视作条件概率嵌套进行理解和计算:
\[\begin{aligned}
H(x^n)&=H(X_{1})+H(X_{2}|X_{1})+\dots+H(X_{n}|x_{1},\dots X_{n-1}) \\
&=\sum^n_{i=1}H(X_{i}|x_{1},\dots,X_{i-1}) \\
&=\sum^n_{i=1}H(X_{i}|x^{i-1}) \\
\end{aligned}
\]
2.7 信息熵的基本性质
2.7.1 对称性
当变量 \(x_{1},x_{2},x_{3},\dots,x_{q}\) 的顺序任意互换时,熵函数的值不变,若变量 \(x_{1},x_{2},x_{3},\dots,x_{q}\) 的概率为 \(p_{1},p_{2},p_{3},\dots,p_{q}\),即
\[H(p_{1},p_{2},p_{3},\dots,p_{q})=H(p_{q},\dots,p_{3},p_{2},p_{1})
\]
2.7.2 确定性
当某个分量的概率值为 1 时,此时的信息熵恒定为 0
\[\begin{aligned}
H(1) &=H(1,0)=H(1,0,0)=H(1,0,0,\dots,0) \\
&=-p_{0}\log p_{0}-\sum_{i=1}^{N} p_{i}\log p_{i} \\
&=-1\cdot \log 1-\sum_{i=1}^N \lim_{ p_{i} \to 0 } p_{i}\log p_{i} \\
&=0+0=0
\end{aligned}
\]
2.7.3 非负性
信息熵始终有 \(H(x)\geq 0\)
\[H(P)=H(p_{1},p_{2},p_{3},\dots,p_{q})=-\sum_{i=1}^N p_{i}\log p_{i}\geq 0(p_{i}\leq 1)
\]
2.7.4 扩展性
\[\lim_{ \varepsilon \to 0 } H_{q+1}(p_{1},p_{2},\dots,p_{q}-\varepsilon,\varepsilon)=H_{q}(p_{1},p_{2},\dots,p_{q})
\]
不难证明,当 \(\varepsilon\to0\) 时,\(\lim_{ \varepsilon \to 0 }\varepsilon \log\varepsilon=0\),故上述等式成立
2.7.5 可加性
独立信源 \(X\) 与 \(Y\) 的联合信源的熵分别等于二者熵的和
\[H(XY)=H(X)+H(Y)
\]
proof:
\[\begin{aligned}
已知\sum_{i=1}^n &p_{i}=1,\ \sum_{j=1}^m q_{j}=1,\ \sum_{i=1}^n \sum_{j=1}^m p_{i}q_{j}=1 \\
H(XY)&=-\sum_{i=1}^n \sum_{j=1}^m p_{i}q_{j}\log p_{i}q_{j} \\
&=-\sum_{i=1}^n \sum_{j=1}^m p_{i}q_{j}\log p_{i}-\sum_{i=1}^n \sum_{j=1}^m p_{i}q_{j}\log q_{j} \\
&=-\sum_{j=1}^m q_{j}\sum_{i=1}^n p_{i}\log p_{i}-\sum_{i=1}^n p_{i}\sum_{j=1}^mq_{j}\log q_{j}\ (独立) \\
&= -\sum_{i=1}^n p_{i}\log p_{i}-\sum_{j=1}^m q_{j}\log q_{j} \\
&=H(X)+H(Y)
\end{aligned}
\]
2.7.6 强可加性
两个相互关联的信源 \(X\) 和 \(Y\) 的联合信源的熵等于信源 \(X\) 的熵加上在 \(X\) 已知条件下信源 \(Y\) 的条件熵
不妨假设 \(P(Y=y_{i}|X=x_{i})=p_{ij},0\leq p_{ij}\leq 1\),已知 \(\sum_{i=0}^n p_{i}p_{ij}=q_{j},\sum_{j=0}^m p_{ij}=1\) ,则:
\[H(XY)=H(X)+H(Y|X)
\]
proof:
\[\begin{aligned}
H(XY)&=-\sum_{i=1}^n \sum_{j=1}^m p_{i}p_{ij}\log p_{i}p_{ij} \\
&=-\sum_{i=1}^n \sum_{j=1}^m p_{i}p_{ij}\log p_{i} -\sum_{i=1}^n \sum_{j=1}^m p_{i}p_{ij}\log p_{ij} \\
&=-\sum_{i=1}^n \bigg(\sum_{j=1}^m p_{ij}\bigg)p_{i}\log p_{i} -\sum_{i=1}^n p_{i} \sum_{j=1}^m p_{ij}\log p_{ij} \\
&=-\sum_{i=0}^n p_{i}\log p_{i} -\sum_{i=1}^n p_{i} \sum_{j=1}^m p_{ij}\log p_{ij} \\
&=H(X)+\sum_{i=1}^n p_{i}H(Y|X=x_{i}) \\
&=H(X)+H(Y|X)
\end{aligned}
\]
2.7.7 递增性/递推性
\[H(p_{1},p_{2},\dots,p_{n-1},p_{n}=H(p_{1},p_{2},\dots,p_{n-1}+p_{n})+(p_{n-1}+p_{n})H\left( \frac{p_{n-1}}{p_{n-1}+p_{n}}, \frac{p_{n}}{p_{n-1}+p_{n}} \right)
\]
2.7.8 极值性
最大离散熵定理
\[H(p_{1},p_{2},\dots,p_{q})\leq H\left( \frac{1}{q}, \frac{1}{q},\dots, \frac{1}{q} \right)=\log q
\]
3 信息
3.1 互信息
对于随机变量 \(X,\ Y\),二者的互信息定义为:
\[I(X;Y)=\sum_{x,y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)}=E\left[ \log \frac{p(X,Y)}{p(X)p(Y)} \right]
\]
上述定义中的 \(X,\ Y\) 可以互相调换位置
注意到: \(\frac{p(x,y)}{p(y)}=p(x|y)\),则有:
\[I(X;Y)=\sum_{x,y}p(x,y)\log \frac{p(x|y)}{p(x)}=E\left[ \log \frac{p(X|Y)}{p(X)} \right]
\]
Tip 1: 随机变量 X 与其自身的互信息等于 X 的熵
\[I(X;X)=H(X)
\]
Proof:
\[\begin{aligned}
I(X;X)&=E\left[ \log \frac{p(X,X)}{p(X)p(X)} \right]\\
&=E\left[ \log \frac{p(X)}{p(X)p(X)} \right]\\
&=E\left[ \log \frac{1}{p(X)} \right]\\
&=-E\left[ \log p(X) \right]=H(X)
\end{aligned}
\]
Tip 2: 互信息与信息熵的关系
\[\begin{aligned}
I(X;Y)&=H(X)-H(X|Y),\\
I(X;Y)&=H(Y)-H(Y|X),\\
I(X;Y)&=H(X)+H(Y)-H(X,Y)
\end{aligned}
\]
即互信息可以理解为 \(X,\ Y\) 的信息熵的相同部分
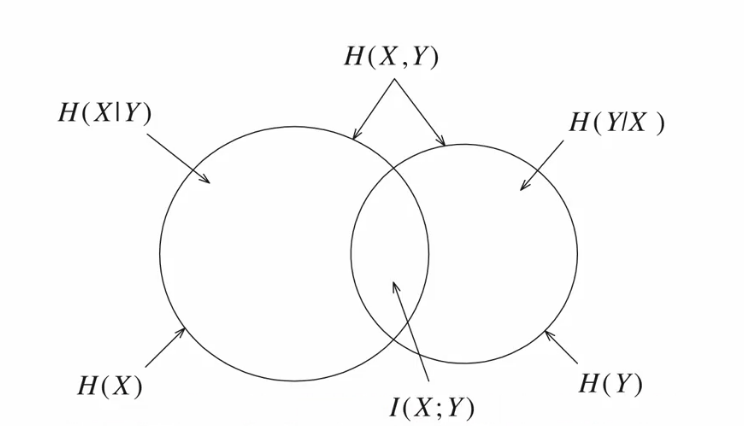
上图中,\(H(X,Y)\) 为两个圆之和,而对应随机变量的熵代表着对应的圆
3.2 条件互信息
对于随机变量 \(X\),\(Y\) 和 \(Z\),当给定 \(Z\) 的时候,三者的互信息定义为:
\[I(X,Y|Z)=\sum_{x,y,z}p(x,y,z)\log \frac{p(x,y|z)}{p(x|z)p(y|z)}=E\left[ \log \frac{p(X,Y|Z)}{p(X|Z)P(Y|Z)} \right]
\]
Tip 1: 条件互信息与互信息的关系
\[\begin{aligned}
I(X;Y|Z)=\sum_{z}&p(z)I(X;Y|Z=z)\\
where\quad I(X;Y|Z=z)&=\sum_{x,y}p(x,y|z)\log \frac{p(x,y|z)}{p(x|z)p(y|z)}
\end{aligned}
\]
Tip 2: 随机变量 Z 为条件下,随机变量 X 与其自身的条件互信息等于给定条件 Z 情况下的 X 的条件熵
\[I(X;X|Z)=H(X|Z)
\]
Tip 3: 基于 2.1 tip 2,我们可以容易进行推广
\[\begin{aligned}
I(X;Y|Z)&=H(X|Z)-H(X|Y,Z),\\
I(X;Y|Z)&=H(Y|Z)-H(Y|X,Z),\\
I(X;Y|Z)&=H(X|Z)+H(Y|Z)-H(X,Y|Z)
\end{aligned}
\]
4 多维随机变量分析 (链式法则)
4.1 无给定条件的熵
对于 \(X_{1},X_{2},\dots X_{n}\),其链式法则的熵为
\[H(X_{1},X_{2},\dots,X_{n})=\sum_{i=1}^nH(X_{i}|X_{1},\dots,X_{i-1})
\]
可以通过条件概率的嵌套理解.
3.2 给定条件的熵
当给定条件 \(Y\) 时, 可以得到条件概率的链式法则的熵为:
\[H(X_{1},X_{2},\dots,X_{n}|Y)=\sum_{i=1}^nH(X_{i}|X_{1},\dots,X_{i-1},Y)
\]
Proof:
\[\begin{aligned}
H(X_{1},X_{2},\dots,X_{n}|Y)&=H(X_{1},X_{2},\dots, X_{n},Y)-H(Y) \\
&=H((X_{1}, Y),X_{2},\dots,X_{n})-H(Y) \\
&=H(X_{1}, Y)+H(X_{2}, X_{3}, \dots, X_{n}|X_{1}, Y)-H(Y) \\
&=\sum_{i=2}^nH(X_{i}|X_{1},\dots,X_{i-1},Y)+H(X_{1},Y)-H(Y) \\
&=\sum_{i=2}^nH(X_{i}|X_{1},\dots,X_{i-1},Y)+H(X_{1}|Y) \\
&=\sum_{i=1}^nH(X_{i}|X_{1},\dots,X_{i-1},Y)
\end{aligned}
\]
或者从无给定条件的熵来看,无给定条件的熵本质是在全部条件 \(\Omega\) 下成立,即
\[H(X_{1},X_{2},\dots,X_{n}|\Omega)=\sum_{i=1}^nH(X_{i}|X_{1},\dots,X_{i-1},\Omega)
\]
将 \(\Omega\) 换成条件 \(Y\) 即可得到:
\[H(X_{1},X_{2},\dots,X_{n}|Y)=\sum_{i=1}^nH(X_{i}|X_{1},\dots,X_{i-1},Y)
\]
4.3 无给定条件的互信息
对于 \(X_{1},X_{2},\dots X_{n}\) 与 \(Y\) 之间的互信息,我们定义其互信息为:
\[I(X_{1},X_{2},\dots,X_{n};Y)=\sum_{i=1}^nI(X_{i};Y|X_{1},X_{2},\dots,X_{i-1})
\]
4.4 给定条件的互信息
对于 \(X_{1},X_{2},\dots X_{n}\) 与 \(Y\) 之间的互信息,若给定了条件 \(Z\),我们定义此时的互信息为:
\[I(X_{1},X_{2},\dots,X_{n};Y)=\sum_{i=1}^nI(X_{i};Y|X_{1},X_{2},\dots,X_{i-1},Z)
\]
5 离散无记忆的扩展信源
而对于 \(N\) 维平稳、离散无记忆信源称为离散无记忆信源 \(X\) 的 \(N\) 次扩展信源,其概率 \(P(a_{i})\) 为各随机变量出现 \(a_{i}\) 的概率积:
\[\begin{gather*}
\begin{bmatrix}
X^N \\
P(a_{i})
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q^N} \\
P(a_{1}), P(a_{2}),\dots, P(a_{q^N})
\end{bmatrix} \\
P(a_{i})=\prod_{i_{k}=1}^q P(a_{i_{k}})
\\
且\ \sum_{i=1}^{q^N} P(a_{i})=\sum_{i=1}^{q^N} \prod_{i_{k}=1}^q P(a_{i_{k}})=1
\end{gather*}
\]
且对于离散无记忆的扩展信源,其信息熵为:
\[H(X^N)=NH(X)
\]
6 离散平稳信源
6.1 一维离散平稳信源
对于一般的离散信源,其在 \(t=i\) 时刻的输出符号取决于:
- 信源在 \(t=i\) 时刻的随机变量 \(X_{i}\) 的取值的概率分布 \(P(x_{i})\)
- 信源在 \(t=i\) 时刻以前输出的符号,即与条件概率 \(P(x_{i}|x_{i-1}x_{i-2}\dots)\) 有关
上述两个概率对于一般的离散信源而言,都与时间 \(t\) 有关,不同时刻下其概率也不同,例如对于时刻 \(i\) 与时刻 \(j\) 而言:
\[P(x_{i})\neq P(x_{j})(i\neq j)
\]
但是对于平稳信源而言,不同时刻的的概率是相同的,即无论在什么时刻,信源输出某一符号的概率始终保持不变:
\[\begin{gather*}
P(x_{i}=a_{1})=P(x_{j}=a_{1})=P(a_{1}) \\
P(x_{i}=a_{2})=P(x_{j}=a_{2})=P(a_{2}) \\
\dots \\
P(x_{i}=a_{n})=P(x_{j}=a_{n})=P(a_{n}) \\
\end{gather*}
\]
对于 \(N\) 阶信源,同样有
\[P(x_{i}x_{i+1}\dots x_{i+N})=P(x_{j}x_{j+1}\dots x_{j+N})
\]
此时,我们称这种离散符号输出的概率分布与输出时刻无关的信源称为离散平稳信源
同样的,对于信源中各个符号间的依赖分布也与时刻无关,即条件概率满足:
\[P(x_{i+N}|x_{i}x_{i+1}\dots x_{i+N-1})=P(x_{j+N}|x_{j}x_{j+1}\dots x_{j+N-1})=P(x_{N}|x_{0}x_{1}\dots x_{N-1})
\]
6.2 二维离散平稳信源及其信息熵
6.2.1 二维离散平稳信源
容易知道,假设二维离散平稳信源的概率空间为:
\[\begin{bmatrix}
X \\
P(x)
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q} \\
P(a_{1}), P(a_{2}), \dots, P(a_{q})
\end{bmatrix} \quad
且\ \sum_{i=1}^q P(a_{i})=1
\]
对于二维离散平稳信源,其连续两个符号出现的联合概率分布为 \(P(a_{i}a_{j})(i,j=1,2,\dots,q)\),且已知 \(0\leq P(a_{i}a_{j})\leq 1\),\(\sum_{i=1}^q \sum_{j=1}^q P(a_{i}a_{j})=1\) (完备集),则由条件概率可知:
\[P(a_{j}|a_{i})=\frac{P(a_{i}a_{j})}{P(a_{i})}(P(a_{i})\neq 0)
\]
显然,\(0\leq P(a_{j}|a_{i})\leq 1\),\(\sum_{j=1}^q P(a_{j}|a_{i})=1\) ,可以发现连续两个符号之间存在依赖关系 (条件概率)
6.2.2 二维离散平稳信源的信息熵
对于二维离散平稳信源,不妨让其连续两个符号组成一个新的离散无记忆信源,其联合概率分布为:
\[\begin{bmatrix}
X_{1}X_{2} \\
P(x_{1}x_{2})
\end{bmatrix}
=
\begin{bmatrix}
a_{1}a_{1}, a_{1}a_{2},\dots, a_{q-1}a_{q}, a_{q}a_{q} \\
P(a_{i}a_{j})=P(a_{i})P(a_{j}|a_{i})
\end{bmatrix} \quad
且\ \sum_{i=1}^q \sum_{j=1}^q P(a_{i}a_{j})=1\ (P(a_{i}a_{j})\geq 0)
\]
则由信息熵的定义,二维离散平稳信源的信息熵为:
\[H(X_{1}X_{2})=\sum_{i=1}^q \sum_{j=1}^q P(a_{i}a_{j})\log \frac{1}{P(a_{i}a_{j})}=-\sum_{i=1}^q \sum_{j=1}^q P(a_{i}a_{j})\log P(a_{i}a_{j})
\]
另外,我们可以从二维离散平稳信源的定义中了解到,在该信源中连续两个符号之间存在依赖关系,结合信息熵的定义,显然:
如果我们已知当前时刻信源输出的符号,则下一时刻信源所输出的符号具有不确定性,即具有信息熵
此时,我们称其为条件熵
对于该二维离散平稳信源,当已知输出符号 \(X_{1}=a_{i}\) 时,下一符号的不确定性 \(H(X_{2}|X_{1}=a_{i})\) 为:
\[H(X_{2}|X_{1}=a_{i})=-\sum_{j=1}^q P(a_{j}|a_{i})\log P(a_{j}|a_{i})
\]
注意到,信源输出符号 \(X_{1}=a_{i}\) 同样是有概率的,我们可以观察到 \(X_{1}=a_{i}\) 与 \(H(X_{2}|X_{1}=a_{i})\) 同样可以组成一对概率分布,此时我们对 该符号 与 不确定性 组成的的概率分布求期望,得到的熵 \(H(X_{2}|X_{1})\),称为条件熵:
\[\begin{aligned}
H(X_{2}|X_{1})&=-\sum_{i=1}^q P(a_{i})H(X_{2}|X_{1}=a_{i}) \\
&=-\sum_{i=1}^q \sum_{j=1}^q P(a_{i})P(a_{j}|a_{i})\log P(a_{j}|a_{i}) \\
&=-\sum_{i=1}^q \sum_{j=1}^q P(a_{i}a_{j})\log P(a_{j}|a_{i})
\end{aligned}
\]
另外,我们可以知道:
\[H(X_{1}X_{2})=H(X_{1})+H(X_{2}|X_{1})
\]
Proof:
\[\begin{aligned}
H(X_{1}X_{2})&=-\sum_{i=1}^q \sum_{j=1}^q P(a_{i}a_{j})\log P(a_{i}a_{j}) \\
&=-\sum_{i=1}^q \sum_{j=1}^q P(a_{i})P(a_{j}|a_{i})\log [P(a_{i})P(a_{j}|a_{i})] \\
&=-\sum_{i=1}^q \sum_{j=1}^q \bigg( P(a_{i})P(a_{j}|a_{i})\log P(a_{i}) +P(a_{i})P(a_{j}|a_{i})\log P(a_{j}|a_{i}) \bigg) \\
&=-\sum_{i=1}^q \bigg( P(a_{i})\log P(a_{i}) \bigg) \sum_{j=1}^q P(a_{j}|a_{i}) - \sum_{i=1}^q\sum_{j=1}^q P(a_{i})P(a_{j}|a_{i}) \log P(a_{j}|a_{i}) \\
&\left( 其中\sum_{j = 1}^q P(a_{j}|a_{i})=1 \right) \\
&=-\sum_{i=1}^q P(a_{i})\log P(a_{i}) + H(X_{2}|X_{1}) \\
&=H(X_{1})+H(X_{2}|X_{1})
\end{aligned}
\]
这也是熵的强可加性的体现
另外,有条件熵与无条件熵的关系为:
\[H(X_{2}|X_{1})\leq H(X_{2})
\]
从理论上解释,条件熵相比于无条件熵多出了一个已知条件,这在一定程度上减少了信息的不确定性,当且仅当 \(P(a_{j}|a_{i})=P(a_{j})(P(a_{i}) = 1)\) 时,等号成立
所以,可以推导出:
\[H(X_{1}X_{2})=H(X_{1})+H(X_{2}|X_{1})\leq H(X_{1})+H(X_{2})
\]
6.2.3 离散平稳信源的极限熵
在一般的离散平稳有记忆信源中,符号的相互依赖关系可能不仅存在于相邻两个符号之间,而是扩展到多个符号,不妨假顶信源符号的依赖长度为 \(N\),设离散有记忆信源的概率分布为:
\[\begin{bmatrix}
X \\
P(x)
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q} \\
P(a_{1}), P(a_{2}), \dots, P(a_{q})
\end{bmatrix} \quad
且\ \sum_{i=1}^q P(a_{i})=1
\]
对于该平稳信源,已知其概率分布与时间无关,且当符号长度 \(L\leq N\) 时,其概率分布和始终为 \(1\),即:
\[\begin{cases}
P(x_{1}x_{2})=P(x_{1}=a_{i_{1}}\ x_{2}=a_{i_{2}}) \\
P(x_{1}x_{2}x_{3})=P(x_{1}=a_{i_{1}}\ x_{2}=a_{i_{2}\ x_{3}=a_{i_{3}}}) \\
\dots \\
P(x_{1}x_{2}\dots x_{N})=P(x_{1}=a_{i_{1}}\ x_{2}=a_{i_{2}}\dots\ x_{N}=a_{i_{N}})
\end{cases}
\ 且\
\begin{cases}
\sum_{i_{1}=1}^q \sum_{i_{2}=1}^q P(a_{i_{1}}a_{i_{2}})=1 \ (P(a_{i_{1}}a_{i_{2}})\geq 0) \\
\sum_{i_{1}=1}^q \sum_{i_{2}=1}^q \sum_{i_{3}=1}^q P(a_{i_{1}}a_{i_{2}}a_{i_{3}})=1 \ (P(a_{i_{1}}a_{i_{2}}a_{i_{3}})\geq 0) \\
\dots \\
\sum_{i_{1}=1}^q \sum_{i_{2}=1}^q \dots \sum_{i_{N}=1}^q P(a_{i_{1}}a_{i_{2}}\dots a_{i_{N}})=1 \ (P(a_{i_{1}}a_{i_{2}}\dots a_{i_{N}})\geq 0)
\end{cases}
\]
则该信源的联合信息熵 \(H(X_{1}X_{2}\dots X_{N})\) 为:
\[H(X_{1}X_{2}\dots X_{N})=-\sum_{i_{1}=1}^q \dots \sum_{i_{N}=1}^q P(a_{i_{1}}a_{i_{2}}\dots a_{i_{N}})\log P(a_{i_{1}}a_{i_{2}}\dots a_{i_{N}})
\]
而该信源的符号平均信息熵为:
\[H_{N}(X)=\frac{1}{N}H(X_{1}X_{2}\dots X_{N})
\]
称其为平均信息熵
另外,根据6.2.2中条件熵的阐述,在该符号依赖长度位 \(N\) 的信源中也有条件熵为:
\[H(X_{N}|X_{1}X_{2}\dots X_{N-1})=-\sum_{i_{1},i_{2},\dots,i_{N}} P(a_{i_{1}}a_{i_{2}}\dots a_{i_{N}})\log P(a_{i_{N}}|a_{i_{1}}a_{i_{2}}\dots a_{i_{N-1}})
\]
对于离散平稳信源,当 \(H_{1}(X)<\infty\) 时,有以下性质
- 条件熵 \(H(X_{N}|X_{1}X_{2}\dots X_{N-1})\) 随着 \(N\) 的增加是非递增的
\(N\) 增加,则条件增加,所以 \(X_{N}\) 的不确定性是减少的,当且仅当新增条件的出现概率为 \(1\),不确定性保持不变
- 当 \(N\) 给定时,平均符号条件熵 \(\geq\) 条件熵,即 \(H_{N}(X)\geq H(X_{N}|X_{1}X_{2}\dots X_{N-1})\)
当依赖长度 \(N\) 趋于无穷时,平均符号条件熵等价于此时的条件熵,此时等号成立
- 平均符号熵 \(H_{N}(X)\) 随着 \(N\) 的增加也是非递增的
- \(H_{\infty}=\lim_{ N \to \infty } H_{N}(X)\) 存在,且有
\[H_{\infty}=\lim_{ N \to \infty } H_{N}(X)=\lim_{ N \to \infty } H(X_{N}|X_{1}X_{2}\dots X_{N-1})
\]
称 \(H_{\infty}\) 为离散平稳信源的极限熵或极限信息量,也可以称为离散平稳信源的熵率
长度为 \(m\) 的离散平稳信源极限熵等于有限记忆长度为 \(m\) 的条件熵:
\[\begin{aligned}
H_{\infty}&=\lim_{ N \to \infty } H(X_{N}|X_{1}X_{2}\dots X_{N})=H(X_{m+1}|X_{1}X_{2}\dots X_{m}) \\
&=-\sum_{i_{1}=1}\sum_{i_{2}=1}\dots \sum_{i_{m}=1}\sum_{i_{m+1}=1} P(a_{i_{1}}\dots a_{i_{m}})P(a_{i_{m+1}}|a_{i_{1}}a_{i_{2}}\dots a_{i_{m}})\log P(a_{m+1}|a_{1}a_{2}\dots a_{i_{m}})
\end{aligned}
\]
所以我们对有限记忆长度的离散平稳信源,可以有记忆长度的条件熵对该离散平稳信源进行信息测度
7 马尔可夫信源
7.1 马尔可夫信源的定义
设一般信源所处状态 \(S\in E=\{ E_{1},E_{2},\dots,E_{J} \}\),在每一状态下可能输出的符号 \(X \in A=\{ a_{1},a_{2},\dots,a_{q} \}\),并认为每一时刻,当信源输出一个符号之后,信源所处的状态将发生转移。
不妨假设信源输出的随机序列符号为:
\[x_{1},x_{2},\dots,x_{l-1},x_{l},\dots
\]
信源所处的随即状态序列为:
\[s_{1},s_{2},\dots,s_{l-1},s_{l},\dots
\]
则在第 \(l\) 时刻,信源处于状态 \(E_{i}\) 时,输出符号 \(a_{k}\) 的概率给定为
\[P(x_{l}=a_{k}|s_{l}=E_{i})
\]
另外,假设第 \(l-1\) 时刻时信源处于 \(E_{i}\) 状态,此时他在下一个时刻状态转移到 \(E_{j}\) 的状态转移概率为:
\[P_{ij}(l)=P(s_{l}=E_{j}|s_{l-1}=E_{i})
\]
此时我们认为该信源服从马尔可夫链,即下一个时刻信源处于什么状态只与现在的状态有关,而与以前所处的状态无关。
一般情况下,状态转移概率和已知状态下输出符号的概率与时刻 \(l\) 有关. 当这些概率与时刻 \(l\) 无关时,即满足以下条件:
\[\begin{cases}
P(x_{l}=a_{k}|s_{l}=E_{i})=P(a_{k}|E_{i}) \\
P_{ij}=P(E_{j}|E_{i})
\end{cases}
\]
则称为时齐的或齐次的,此时信源的状态序列服从时齐马尔可夫链
具体而言,满足下列两个条件,即可称信源为时齐马尔可夫信源:
- 某一时刻信源输出的符号只与此刻信源所处状态有关,而和以前的状态及以前的符号无关,即:\(P(x_{l}=a_{k}|s_{l}=E_{i},x_{l-1}=a_{k-1},s_{l-1}=E_{j}\dots)=P(x_{l}=a_{k}|s_{l}=E_{i})\),当具有时齐性时,\(P(x_{l}=a_{k}|s_{l}=E_{i})=P(a_{k}|E_{i})\),且 \(\sum_{a_{k}\in A} P(a_{k}|E_{i})=1\)
- 信源在 \(l\) 时刻所处的状态由当前的输出符号和前一时刻 \((l-1)\) 信源的状态唯一决定,即:\(P(s_{l}=E_{i}|x_{l}=a_{k},s_{l-1}=E_{j})=\begin{cases} 0 \\ 1 \end{cases} \quad E_{i},E_{j}\in E \ and\ a_{k}\in A\)
其中,第 2个条件指出,当信源输出一个符号后,其状态就会发生改变,一定会从一个状态转移到另一个状态去
7.2 时齐 \(m\) 阶马尔可夫信源
对于一阶马尔可夫信源,其任意时刻信源发出符号的概率仅与前面一个符号有关,故称为一阶马尔可夫信源;当时齐马尔可夫信源发出的符号的概率与前面的 \(m\) 个符号有关,则称为时齐 \(m\) 阶马尔可夫信源
\(m\) 阶有记忆非平稳离散信源的数学模型如下:
\[\begin{bmatrix}
X \\
P
\end{bmatrix}
=
\begin{bmatrix}
a_{1}, a_{2},\dots, a_{q} \\
P(a_{k_{m+1}}|a_{k_{1}}a_{k_{2}}\dots a_{k_{m}})
\end{bmatrix} \quad
且\ \sum_{a_{k_{m+1}}=1}^q P(a_{k_{m+1}}|a_{k_{1}}a_{k_{2}}\dots a_{k_{m}})=1
\]
一般情况下,\(m\) 阶马尔可夫信源不是离散平稳信源
7.3 马尔可夫信源的信息熵
一般的马尔可夫信源所输出的符号是非平稳的随机序列,其各维的概率分布可能随着时间的变化而改变。
一般马尔可夫信源的信息熵应该是其平均符号熵的极限值:
\[H_{\infty}=H_{\infty}(X)=\lim_{ N \to \infty } \frac{1}{N}H(X_{1}X_{2}\dots X_{N})
\]
根据前文所述,我们也可以根据依赖关系求出符号的条件熵,不妨计算当信源处于状态 \(E_{i}\) 时,输出一个信源符号所携带的平均信息量,即在状态 \(E_{i}\) 下输出一个符号的条件熵:
\[H(X|s=E_{i})=-\sum_{k=1}^q P(a_{k}|E_{i})\log P(a_{k}|E_{i})
\]
结合上述两个公式,经过复杂的推导可以得到时齐、遍历的马尔可夫信源的熵为:
\[\begin{aligned}
H_{\infty}&=\sum_{i=1}^J Q(E_{i})H(X|E_{i}) \\
&=-\sum_{i=1}^J \sum_{k=1}^q Q(E_{i})P(a_{k}|E_{i})\log O(a_{k}|E_{i})
\end{aligned}
\]
且相关参数满足下列方程:
\[\begin{gather*}
\sum_{E_{j}\in E}Q(E_{j})P(E_{i}|E_{j})=Q(E_{i}) \\
\sum_{E_{i}\in E}Q(E_{i})=1
\end{gather*}
\]
上式中,\(Q(E_{i})\) 是时齐、遍历的马尔可夫链的极限概率.
综上所述,我们可以了解到,当马尔可夫信源的状态转移步长在 \(N\) 以内时,其不同符号出现的概率并没有确定下来,此时的信源所处的随机状态序列不是平稳的。当结果足够长的时间后,符号的概率分布才会达到一种稳定的状态
所以,时齐、遍历的马尔可夫信源在起始的有限时间内,信源输出的随机符号序列不是平稳的;只有经过了足够长的时间后,输出的随机符号序列才可以称为平稳的。因此,时齐、遍历的马尔可夫信源并非是离散平稳有记忆信源
另外,时齐、遍历的 \(m\) 阶马尔可夫信源的熵等于有限记忆长度的为 \(m\) 的条件熵,但它并非是有限记忆长度为 \(m\) 的离散平稳信源
8 信源剩余度
8.1 概念
可以知道,如果信源发出的符号之间没有依赖关系、且等概率分布时,其不确定性最大,信源的熵最大;若信源发出的符号之间存在依赖关系,则每个符号的平均信息量会减少,且依赖长度越长,不确定性越低,平均信息量越低
为了衡量信源发出的符号之间的依赖程度,我们引入信源剩余度来衡量信源符号之间的相关性程度 (也称为冗余度或多余度)
8.2 符号定义
我们首先确定熵的相对率,将信源的实际信息熵与具有相同符号集的最大熵比值称为相对率:
\[\eta = \frac{H_{\infty}}{H_{0}}
\]
信源剩余度等于 \(1\) 减去熵的相对率:
\[\gamma = 1 - \eta = 1 - \frac{H_{\infty}}{H_{0}}
\]
挖坑:到时候找点上课例题放上来写点怎么理解的
还没学完,边学边写/(ㄒoㄒ)/~~
1 Network Information Theory, Abbas El Gamal, Young-Han Kim
2 Information Theory and Network Coding, Raymond W. Yeung
3 信息论——基础理论与应用, 傅祖芸




 浙公网安备 33010602011771号
浙公网安备 33010602011771号