第六章学习小结

整理一下第六章学到的知识

图的定义

图，是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V，E），其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

（线性表中可以没有元素，称为空表。树中可以没有结点，叫做空树。但是在图中不允许没有顶点，可以没有边。）

一些术语：

• 无向边：若顶点Vi和Vj之间的边没有方向，称这条边为无向边（Edge），用（Vi，Vj）来表示。

• 无向图（Undirected graphs）：图中任意两个顶点的边都是无向边。

• 有向边：若从顶点Vi到Vj的边有方向，称这条边为有向边，也称为弧（Arc），用<Vi, Vj>来表示，其中Vi称为弧尾（Tail），Vj称为弧头（Head）。

• 有向图（Directed graphs）：图中任意两个顶点的边都是有向边。

• 简单图：不存在自环（顶点到其自身的边）和重边（完全相同的边）

• 无向完全图：无向图中，任意两个顶点之间都存在边。

• 有向完全图：有向图中，任意两个顶点之间都存在方向相反的两条弧。

• 稀疏图；有很少条边或弧的图称为稀疏图，反之称为稠密图。

• 权（Weight）：表示从图中一个顶点到另一个顶点的距离或耗费。

• 网：带有权重的图

• 度：与特定顶点相连接的边数；

• 出度、入度：有向图中的概念，出度表示以此顶点为起点的边的数目，入度表示以此顶点为终点的边的数目；

• 环：第一个顶点和最后一个顶点相同的路径；

• 简单环：除去第一个顶点和最后一个顶点后没有重复顶点的环；

• 连通图：任意两个顶点都相互连通的图；

• 极大连通子图：包含竟可能多的顶点（必须是连通的），即找不到另外一个顶点，使得此顶点能够连接到此极大连通子图的任意一个顶点；

• 连通分量：极大连通子图的数量；

• 强连通图：此为有向图的概念，表示任意两个顶点a，b，使得a能够连接到b，b也能连接到a 的图；

• 生成树：n个顶点，n-1条边，并且保证n个顶点相互连通（不存在环）；

• 最小生成树：此生成树的边的权重之和是所有生成树中最小的；

 

图的存储结构

邻接矩阵

图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称邻接矩阵）存储图中的边或弧的信息。

无向图由于边不区分方向，所以其邻接矩阵是一个对称矩阵。邻接矩阵中的0表示边不存在，主对角线全为0表示图中不存在自环。

带权有向图的邻接矩阵:

在带权有向图的邻接矩阵中，数字表示权值weight，「无穷」表示弧不存在。由于权值可能为0，所以不能像在无向图的邻接矩阵中那样使用0来表示弧不存在。

优缺点：

• 优点：结构简单,操作方便；
• 缺点：对于稀疏图，这种实现方式将浪费大量的空间。

邻接表

邻接表是一种将数组与链表相结合的存储方法。其具体实现为：将图中顶点用一个一维数组存储，每个顶点Vi的所有邻接点用一个单链表来存储。

对于有向图其邻接表结构如下:

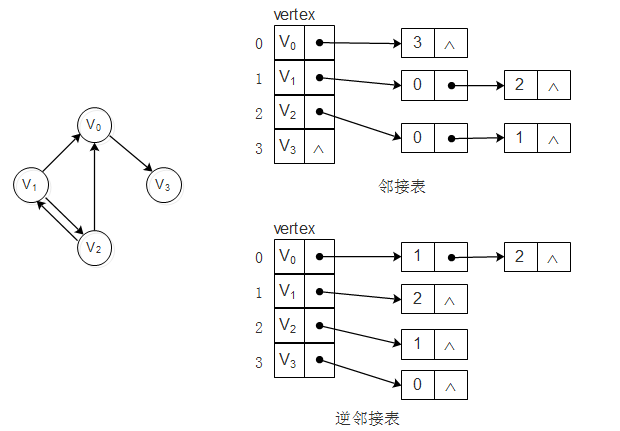
有向图的邻接表是以顶点为弧尾来存储边表的，这样很容易求一个顶点的出度（顶点对应单链表的长度），但若求一个顶点的入度，则需遍历整个图才行。

这时可以建立一个有向图的逆邻接表即对每个顶点v都建立一个弧头尾v的单链表。如上图所示。

邻接表实现比较适合表示稀疏图。

 

图的遍历

从图的某个顶点出发，遍历图中其余顶点，且使每个顶点仅被访问一次，这个过程叫做图的遍历（Traversing Graph）。

对于图的遍历通常有两种方法：深度优先遍历和广度优先遍历。

深度优先遍历

深度优先遍历（DFS），也成为深度优先搜索。

遍历思想：基本思想：首先从图中某个顶点v0出发，访问此顶点，然后依次从v相邻的顶点出发深度优先遍历，直至图中所有与v路径相通的顶点都被访问了；若此时尚有顶点未被访问，则从中选一个顶点作为起始点，重复上述过程，直到所有的顶点都被访问。

深度优先遍历用递归实现比较简单，只需用一个递归方法来遍历所有顶点，在访问某一个顶点时：

• 将它标为已访问
• 递归的访问它的所有未被标记过的邻接点

广度优先遍历

广度优先遍历（BFS），又称为广度优先搜索。

遍历思想：首先，从图的某个顶点v0出发，访问了v0之后，依次访问与v0相邻的未被访问的顶点，然后分别从这些顶点出发，广度优先遍历，直至所有的顶点都被访问完。

 

讲到DFS和BFS，那就顺便把PTA上的列出连通集给摆上来吧：

给定一个有N个顶点和E条边的无向图，请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时，假设我们总是从编号最小的顶点出发，按编号递增的顺序访问邻接点。

输入格式:

输入第1行给出2个整数N(0)和E，分别是图的顶点数和边数。随后E行，每行给出一条边的两个端点。每行中的数字之间用1空格分隔。

输出格式:

按照"{ v​1​​ v​2​​ ... v​k​​ }"的格式，每行输出一个连通集。先输出DFS的结果，再输出BFS的结果。

输入样例:

8 6
0 7
0 1
2 0
4 1
2 4
3 5

输出样例:

{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }

 

那对应上述所讲的DFS和BFS的遍历思想，BFS算法可以结合队列，并且要注意空格的输出。

 

以下是我的代码：

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

int vexnum, arcnum;//顶点数，边数 
int visit[11];//用来判断顶点是否已经访问过 
int Map[11][11];//用来判断两顶点之间是否有边连接 

void DFS(int x)
{
    cout << x << ' ';
    for(int i=0; i<vexnum; i++)
    {
        if(!visit[i] && Map[x][i]==1)//如果该顶点对应的邻接点还未被访问 
        {
            visit[i] = 1;//做好标记 
            DFS(i);//递归调用DFS函数 
        }
    }
}

void BFS(int x)
{
    int y;
    queue <int> Q;//定义一个队列方便之后的操作 
    Q.push(x);
    while(!Q.empty())
    {
        y = Q.front();//获取队列的头元素 
        cout << y << ' ';//输出头元素 
        Q.pop();//头元素出列 
        for(int i=0; i<vexnum; i++)
        {
            if(!visit[i] && Map[y][i]==1)//如果该顶点对应的邻接点还未被访问
            {
                visit[i] = 1;//做好标记
                Q.push(i);//邻接点入队 
            }
        }
    }
}

int main()
{
    int x,y;
    
    cin >> vexnum >> arcnum;
    
    memset(Map, 0, sizeof(Map));//利用menset函数将Map数组的值全赋为0 
    memset(visit, 0, sizeof(visit));//利用menset函数将v数组的值全赋为0
    
    while(arcnum--)
    {
        cin >> x >> y;
        Map[x][y] = Map[y][x] = 1;//注意是“无向” 
    }
    
    for(int i=0; i<vexnum; i++)
    {
        if(visit[i] == 0)//如果还未访问 
        {
            visit[i] = 1;
            cout << "{ ";
            DFS(i);
            cout << "}" << endl;//注意空格的输出问题 
        }
    }
    
    memset(visit, 0, sizeof(visit));//利用menset函数将v数组的值重新全赋为0
    
    for(int i=0; i<vexnum; i++)
    {
        if(visit[i] == 0)
        {
            visit[i] = 1;
            cout << "{ ";
            BFS(i);
            cout << "}" << endl;//注意空格的输出问题 
        }
    }
    
    return 0;
}