二次剩余系解法
(Note: All  are taken to mean
are taken to mean 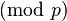 , unless indicated otherwise).[edit]The algorithm
, unless indicated otherwise).[edit]The algorithm
Inputs: p, an odd prime. n, an integer which is a quadratic residue (mod p), meaning that the Legendre symbol  .
.
Outputs: R, an integer satisfying  .
.
- Factor out powers of 2 from p − 1, defining Q and S as:
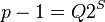 with Q odd. Note that if
with Q odd. Note that if  , i.e.
, i.e. 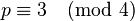 , then solutions are given directly by
, then solutions are given directly by  .
. - Select a z such that the Legendre symbol
 (that is, z should be a quadratic non-residue modulo p), and set
(that is, z should be a quadratic non-residue modulo p), and set  .
. - Let
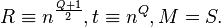
- Loop:
- If
 , return R.
, return R. - Otherwise, find the lowest i,
 , such that
, such that  ; e.g. via repeated squaring.
; e.g. via repeated squaring. - Let
 , and set
, and set 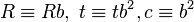 and
and 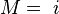 .
.
- If
Once you have solved the congruence with R the second solution is p − R.
Example
Solving the congruence  . It is clear that
. It is clear that  is odd, and since
is odd, and since  , 10 is a quadratic residue (by Euler's criterion).
, 10 is a quadratic residue (by Euler's criterion).
- Step 1: Observe
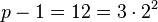 so
so  ,
, 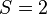 .
.
- Step 2: Take
 as the quadratic nonresidue (2 is a quadratic nonresidue since
as the quadratic nonresidue (2 is a quadratic nonresidue since 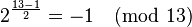 (again, Euler's criterion)). Set
(again, Euler's criterion)). Set 
- Step 3:
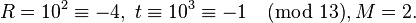
- Step 4: Now we start the loop:
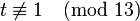 so
so  ; i.e.
; i.e. 
- Let
 , so
, so  .
. - Set
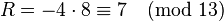 . Set
. Set  , and
, and 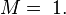
- We restart the loop, and since
 we are done, returning
we are done, returning 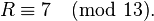
- Let
Indeed, observe that 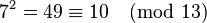 and naturally also
and naturally also  . So the algorithm yields two solutions to our congruence.
. So the algorithm yields two solutions to our congruence.
Proof
First write 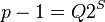 . Now write
. Now write 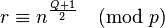 and
and  , observing that
, observing that 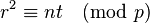 . This latter congruence will be true after every iteration of the algorithm's main loop. If at any point,
. This latter congruence will be true after every iteration of the algorithm's main loop. If at any point, 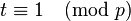 then
then  and the algorithm terminates with
and the algorithm terminates with  .
.
If 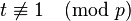 , then consider
, then consider  , a quadratic non-residue of
, a quadratic non-residue of  . Let
. Let  . Then
. Then  and
and  , which shows that the order of
, which shows that the order of  is
is 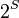 .
.
Similarly we have 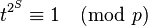 , so the order of
, so the order of  divides
divides 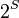 . Suppose the order of
. Suppose the order of  is
is  . Since
. Since  is a square modulo
is a square modulo  ,
,  is also a square, and hence
is also a square, and hence  .
.
Now we set  and with this
and with this  ,
, 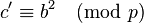 and
and 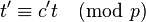 . As before,
. As before, 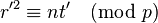 holds; however with this construction both
holds; however with this construction both  and
and 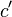 have order
have order  . This implies that
. This implies that  has order
has order  with
with  .
.
If  then
then 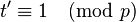 , and the algorithm stops, returning
, and the algorithm stops, returning 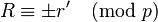 . Else, we restart the loop with analogous definitions of
. Else, we restart the loop with analogous definitions of 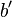 ,
, 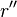 ,
,  and
and  until we arrive at an
until we arrive at an  that equals 0. Since the sequence of S is strictly decreasing the algorithm terminates.
that equals 0. Since the sequence of S is strictly decreasing the algorithm terminates.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号