计算机视觉——图像处理基础
一、图像轮廓和直方图
1.1原理
图像轮廓:因为绘制轮廓需要对每个坐标的像素值施加一个阈值,所以首先需要将图像灰度化。
直方图:用来表征该图像像素值得分布情况。用一定的小区间来指定表征像素值的范围,每个小区间会得到落入该小区间表示范围的像素数目。——》hist()函数:参数二:指定小区间的数目。参数一:只接受一维数组作为输入,因此在绘制图像直方图前,必须对图像进行压平处理。
1.1图像轮廓和直方图得实现
在原点的左上角显示轮廓图像 contour(im,origin='image')。
# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)
im = array(Image.open(r'C:\Users\mangowu\Desktop\1\1.jpg').convert('L')) # 打开图像,并转成灰度图像
figure()
subplot(121)
gray()
contour(im, origin='image')
axis('equal')
axis('off')
title(u'图像轮廓', fontproperties=font)
subplot(122)
hist(im.flatten(), 128)
title(u'图像直方图', fontproperties=font)
plt.xlim([0,260])
plt.ylim([0,11000])
show()
1.3实现效果

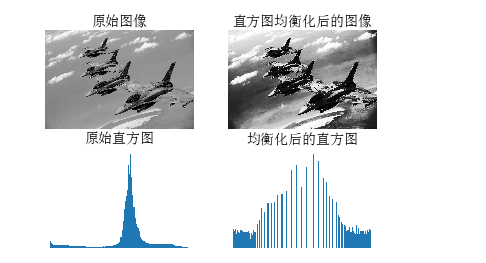
二、直方图的均衡化
2.1 原理
直方图均衡化的计算过程
- 得到原始图片的灰度直方图
- 得到各个灰度级对应的概率密度函数
- 通过概率密度函数得到累积分布函数
- 累计分布函数乘以255,得到每一个灰度级对应的新的灰度
- 通过第4步的结果,将旧灰度映射得到新的灰度,即更新整张图片的灰度
2.2 直方图均衡化的实现
直方图均衡化函数:histeq()。histeq():用于增强灰度值动态范围偏小的图像的对比度,从而实现直方图的均衡化。
from PIL import Image
from pylab import *
from PCV.tools import imtools
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)
im = array(Image.open('C:/Users/mangowu/Desktop/1/1.jpg').convert('L')) # 打开图像,并转成灰度图像
im2,cdf = imtools.histeq(im)
figure()
subplot(2, 2, 1)
axis('off')
gray()
title(u'原始图像', fontproperties=font)
imshow(im)
subplot(2, 2, 2)
axis('off')
title(u'直方图均衡化后的图像', fontproperties=font)
imshow(im2)
subplot(2, 2, 3)
axis('off')
title(u'原始直方图', fontproperties=font)
hist(im.flatten(), 128, normed=True)
subplot(2, 2, 4)
axis('off')
title(u'均衡化后的直方图', fontproperties=font)
hist(im2.flatten(), 128, normed=True)
show()
2.3实现效果
三、高斯滤波
3.1原理
高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,广泛应用于图像处理的减噪过程。高斯滤波是对整幅图像进行加权平均的过程,每一个像素点的值,都由其本身和领域内的其他像素值经过加权平均后得到。
高斯滤波的具体操作:用一个模板扫描图像中的每一个像素,用模板确定的领域内像素的加权平均灰度值去替代模板中心像素点的作用。
对于图像来说,进行平滑和模糊,就是利用周边像素的平均值。
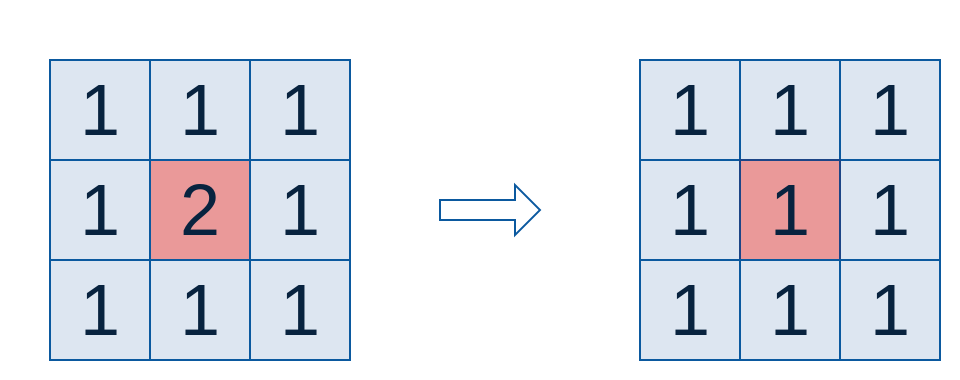
中间点取周围点的平均值,在图形上相当于产生了模糊的效果,中间的失去了细节。
二、高斯滤波实现
使用快速一维分离的方式来计算卷积 filters.gaussian_filter(im, 10) 第二个参数越大,图像越模糊
# encoding:utf-8
from PIL import Image
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
from numpy import *
from scipy.ndimage import filters
from PCV.tools import rof
im = array(Image.open(r'C:\Users\mangowu\Desktop\1\1.jpg').convert('L'))
U, T = rof.denoise(im, im)
G = filters.gaussian_filter(im, 10) # 第二个参数越大,图像越模糊
figure()
gray()
subplot(1, 3, 1)
imshow(im)
#axis(‘equal’)
axis('off')
title(u'原噪声图像')
subplot(1, 3, 2)
imshow(G)
#axis(‘equal’)
axis('off')
title(u'高斯模糊后的图像')
subplot(1, 3, 3)
imshow(U)
#axis(‘equal’)
axis('off')
title(u'ROF降噪后的图像')
show()
三、实现效果

四、总结
对图像的操作与matlab方法相似,易于理解。python很多操作调用各种库里封装好的函数,易于操作和实现。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号