MDP-马尔可夫决策过程

马尔可夫决策过程（MDP）的原始模型是马尔可夫链（Markov Chain, MC），下面先学习一些MC的内容：

1. 马尔可夫性当前状态包含了对未来预测所需要的有用信息，过去信息对未来预测不重要，该就满足了马尔科夫性，严格来说，就是某一状态信息包含了所有相关的历史，只要当前状态可知，所有的历史信息都不再需要，当前状态就可以决定未来，即Xt只与Xt-1有关，与{X0，X1,X2.....,Xt-2}无关，则认为该状态具有马尔科夫性。而具有马尔可夫性的序列X= {X0,X1.......,Xt,....}就是马尔可夫链。 。用公式描述：

\[\mathbb{P}\left[S_{t+1} \mid S_{t}\right]=\mathbb{P}\left[S_{t+1} \mid S_{1}, \ldots, S_{t}\right]\ \]

2. 离散状态的马尔可夫链：由定义在S空间的随机变量Xt（t= 0，1，2....）转移概率Pij。

   Pij= （Xt =i | Xt-1=j）,i=1,2,..... j=1,2......

   其转移概率Pij可表示为状态转移矩阵：P，满足Pij>=0 且矩阵P的列向量之和为1.

\[\mathcal{P}=\text { from }\left[\begin{array}{ccc} \mathcal{P}_{11} & \ldots & \mathcal{P}_{1 n} \\ \vdots \\ \mathcal{P}_{n 1} & \ldots & \mathcal{P}_{n n} \end{array}\right]\]

3. 马尔可夫链 X 在t时刻的状态分布可由（t-1）时刻的状态状态转移概率决定：

\[\pi(t)=P \pi(t-1)\ \]

马尔可夫链在t时刻的状态分布可以通过递推公式\(\pi(t)=P^{t} \pi(0)\)得到，\(P^{t}\)是表明0时刻从状态j出发，时刻t到达i状态的t步状态转移概率矩阵，其为随机矩阵，表明马尔可夫链的状态是由初始分布和转移概率
分布决定的，P矩阵可以随着时刻发生变化。

4. MC的平稳分布： 对于一个马尔可夫链\(X = \left \{ X_{0}, X_{1},...,X_{t},... \right \}\) 存在一个状态\(\pi ^{T } =\left [ \pi_{1} , \pi_{2},\pi_{3} ...\right ]\)，使得\(\pi = P\pi\)则\(pi\)为该马尔可夫链的平稳分布，MDP假设了该马氏链存在平稳分布，切迭代的最终结果就是找到其平稳分布。

5. MC的一些性质：

   • 不可约性：如果一个马尔可夫链的状态空间仅有一个连通类，即状态空间的全体成员，则该马尔可夫链是不可约的，马尔可夫链的不可约性意味着在其演变过程中，随机变量可以在任意状态间转移 。
   • 非周期：一个MC,不存在一个状态，从这一个状态出发，再返回这个状态所经历的时长具有周期性，定理： 不可约和非周期的有限状态马尔可夫链，有唯一的平稳分布。
   • 正常返：对于任意一个状态，从任意的其他状态出发，时间趋于无穷时，第一次到达该状态的概率大于0（无限状态的MC），定理： 不可约，非周期和正常返马尔可夫链，有唯一的平稳分布。
   • 遍历性：若一个马尔可夫链是不可还原的，且有某个状态是遍历的，则该马尔可夫链的所有状态都是遍历的，被称为遍历链。当时间趋于无穷时，遍历链的状态趋于平稳状态，时间均值趋于空间均值（数学期望）。　　　　　　　　　　

马尔科夫过程 Markov Process

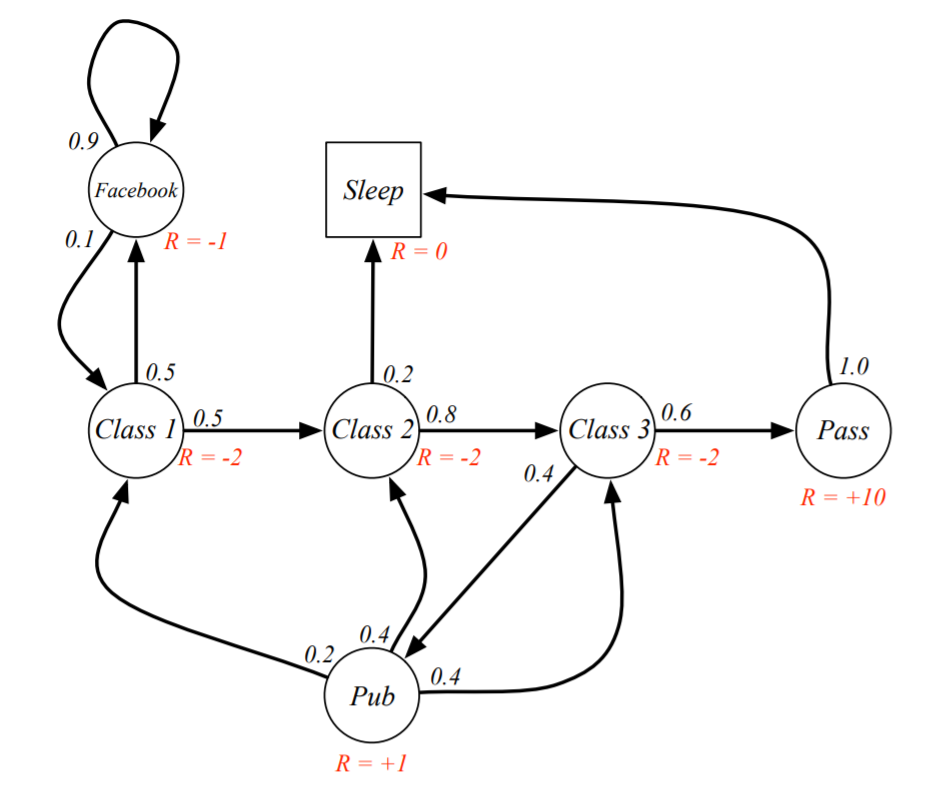
1. 例一：关于学生的马尔可夫链<S,P>,S为状态，P为状态转移矩阵：
   
   其状态转移矩阵如下：

\[\begin{array}{c|ccccc|} & C 1 & C 2 & C 3 & \text { Pass } & \text { Pub } & F B & \text { Sleep } \\ & C 1 & & 0.5 & & & & 0.5 & \\ & C & & & 0.8 & & & & 0.2 \\ & C 3 & & & & 0.6 & 0.4 & & \\ \mathcal{P}= & \text {Pass} & & & & & & & 1.0 \\ & \text {Pub} & 0.2 & 0.4 & 0.4 & & & & \\ & \text {FB} & 0.1 & & & & & 0.9 & \\ & \text {Sleep} & & & & & & & 1 \end{array}\]

其状态转移过程举例如下：当一个学生在上class2时，他有20%的概率睡觉，80%的概率继续听class3.

马尔科夫奖励过程 Markov Reward Process

MRP在MP的基础增加了奖励R（Reward），和衰减系数γ：<S,P,R,γ>。R是一个奖励函数 \(R= \mathbb{E}\left[R_{t+1} \mid S_{t}=s\right]\)， S状态下的奖励是某一时刻(t)处在状态s下在下一个时刻(t+1)能获得的奖励期望。衰减系数 Discount Factor: γ∈ [0, 1], 当γ趋近于0时，会获得一个重视此时刻的评估，当γ趋近于1时，获得一个可以重视远处的评估。从t时刻的收获\(G_{t}\)公式中可以直观感受：

\[G_{t}=R_{t+1}+\gamma R_{t+2}+\ldots=\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \]

价值函数 Value Function：\(v(s)=\mathbb{E}\left[G_{t} \mid S_{t}=s\right]\) 以加入R和γ的学生上课为例

Bellman 方程
对于价值\(V_{(S)}\)的推导：

\[\begin{aligned} v(s) &=\mathbb{E}\left[G_{t} \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right] \end{aligned}\]

最后一行\(G_{t+1}\)变成了 \(V_{(S+1)}\) ,其理由是收获的期望等于收获的期望的期望。
根据推导公式可以得到MRP的Bellman公式：\(v(s)=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right]\)
离散空间的Bellman方程整理得：\(v(s)=\mathcal{R}_{s}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}} v\left(s^{\prime}\right)\)
用矩阵表示bellman方程：v = R + γPv

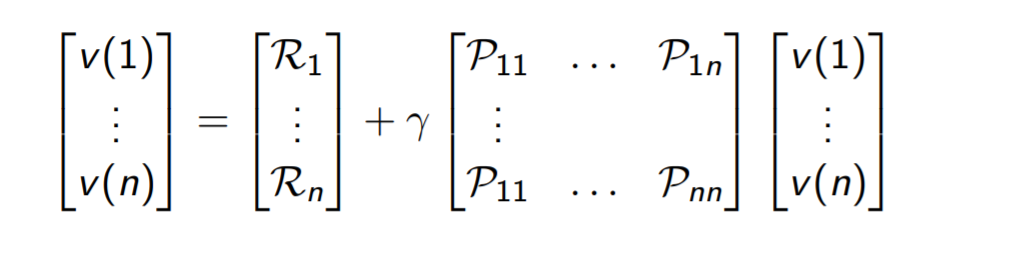
那么这个问题就变成了一个线性方程组的问题：\(V = (E+γP)^{-1}R\)

马尔科夫决策过程 Markov Decision Process
MDP在MRP的基础上增加了变量A（action）表示为<S,A,P,R,γ> ,A表示有限的行为集合。此时的状态转移矩阵\(\mathcal{P}_{s s^{\prime}}^{a}=\mathbb{P}\left[S_{t+1}=s^{\prime} \mid S_{t}=s, A_{t}=a\right]\),奖励函数为\(\mathcal{R}_{s}^{a}=\mathbb{E}\left[R_{t+1} \mid S_{t}=s, A_{t}=a\right]\)。
策略Policy：策略 \(\pi\)是概率的集合或分布，其元素 \(\pi(a|s)\) 为对过程中的某一状态s采取可能的行为a的概率:\(\pi(a \mid s)=\mathbb{P}\left[A_{t}=a \mid S_{t}=s\right]\) 。一个策略完整定义了个体的行为方式，也就是说定义了个体在各个状态下的各种可能的行为方式以及其概率的大小。Policy仅和当前的状态有关，与历史信息无关；同时某一确定的Policy是静态的，与时间无关；但是个体可以随着时间更新策略。
定义\(q_{\pi}(s,a)\)为行为价值函数，表示在执行策略π时，对当前状态s执行某一具体行为a所能的到的收获的期望；或者说在遵循当前策略π时，衡量对当前状态执行行为a的价值大小。行为价值函数一般都是与某一特定的状态相对应的，更精细的描述是状态行为对价值函数。行为价值函数的公式描述如下：

\[q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \]

Bellman期望方程 Bellman Expectation Equation
与上面的MRP的价值函数类似，通过递推可以得到MDP下的状态价值函数和行为价值函数：

\[v_{\pi}(s)=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \]

\[q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \]

最优价值函数：
最优状态价值函数：\(v_{*}=\max _{\pi} v_{\pi}(s)\)
最优行为价值函数: \(q_{*}(s, a)=\max _{\pi} q_{\pi}(s, a)\)
可以通过最大化最优行为价值函数来找到最优策略,对于任何MDP问题，总存在一个确定性的最优策略(个人理解为这里是存在一个唯一的平稳分布)：

\[\pi_{*}(a \mid s)=\left\{\begin{array}{ll} 1 & \text { if } a=\underset{a \in \mathcal{A}}{\operatorname{argmax}} q_{*}(s, a) \\ 0 & \text { otherwise } \end{array}\right.\]

Bellman最优方程 Bellman Optimality Equation

\[v_{*}(s)=\max _{a} q_{*}(s, a)==\max _{a} \mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right) \]

Bellman最优方程是非线性的，没有固定的解决方案，通过一些迭代方法来解决：价值迭代、策略迭代、Q学习、Sarsa等。