素数相关
- 欧拉筛法
- 用数组v[i]来记录这个数的最小质因子
- 依次考虑2-n这些数
- 如果v[i] = i,表示这个数为素数,把这个数存起来
- 否则,扫描所有小于等于v[i]的素数,令v[ip] = p,表示ip这个数的最小质因子是p,被p给筛掉了,这样每个合数就只会被筛一次
点击查看代码
//时间复杂度为O(n)
int prime[300010];
bool vis[4000010];
int cnt = 0;
void Euler_prime(int m)
{
for(int i=2;i<=m;++i)
{
if(cnt>200000) break;//控制打表的质数。
if(!vis[i])
{prime[++cnt]=i;vis[i] = true;}//vis[i]置为true或不置true都可以
for(int j=1;j<=cnt;++j)
{
if(i*prime[j]>m)//判断是否越界
break;
vis[i*prime[j]]=true;//筛数
if(i%prime[j]==0)//时间复杂度为O(n)的关键!
break;
}
}
}
//质因数分解
for(int i = 1;i<=200000;i++)
{
if(prime[i]>sqrt(x)) break;
if(x%prime[i]==0) cout<<prime[i]<<" ";
while(x%prime[i]==0){
x/=prime[i];
}
}
if(x>1) cout<<x;//任意一个正整数n最多只有一个质因数大于根号n
-
素数的性质
1.1~n范围内的素数个数大约为n/ln(n)个
2.素数的分布整体上来说随着数的增大而越来越稀疏,但存在局部的紧密。 -
算数基本定理
何一个大于1的自然数 ,如果N不为质数,都可以唯一分解成有限个质数的乘积 ,这里![image]()
这里![image]() 均为质数,其诸指数
均为质数,其诸指数![image]() 是正整数。
是正整数。
由这个定理易得一个数的正因子个数:![image]()
全体正因子之和:![image]()
例题
给定两个整数L,R,求[L,R]内相邻两个质数的最大差值,(L,R<=2^31)(R-L<=1e6).
首先考虑打表,但2e9范围内的素数太多,数组存不下。然后我们考虑暴力去判断区间内的每一个数是否是素数,使用朴素做法,时间复杂度为O(n√n),无法承受。
考虑优化朴素做法,判断一个数是否为质数,实际上只需要判断这个数能否被小于等于√n的素数整除,而不需要把每一个数去枚举一遍,这样只要把小于等于√2e9的素数打一个表,这样复杂度就是O(n+nlogn),是可以承受的。
筛法例题
题目链接:https://ac.nowcoder.com/acm/contest/26656/1021
关注数据范围为1.3e7,nlogn刚好过不了,必须线性。

点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
//筛法
int num;
const int mod = 1e9+7;
int qpow(int a,int cnt){
int ans = 1;
while(cnt){
if(cnt&1) ans = (ans * a)%mod;
cnt>>=1;
a = (a*a)%mod;
}
return ans%mod;
}
int cnt = 0;
int vis[13000010];
int prime[2000000];
void euler(int n){
for(int i = 2;i<=n;i++){
if(!vis[i]){
vis[i] = qpow(i,num);
prime[++cnt] = i;
}
for(int j = 1;j<=cnt;j++){
if(i*prime[j]>n) break;
vis[prime[j]*i] = ((vis[i]%mod)*(vis[prime[j]]%mod))%mod;
if(i%prime[j]==0) break;
}
}
}
signed main(){
cin>>num;
euler(13000010);
int ans = 1;
for(int i = 2;i<=num;i++){
ans = ans^vis[i];
}
cout<<ans<<endl;
}
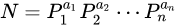
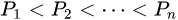 均为质数,其诸指数
均为质数,其诸指数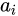 是正整数。
是正整数。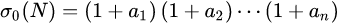
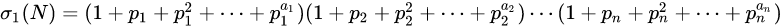

 浙公网安备 33010602011771号
浙公网安备 33010602011771号