8种ADAS横向控制算法PID、Pure Pursuit、Stanley、LQR、MPC、RearWheelFk对比较

一、概述：

本文主要讲解常见的8种自动驾驶系统横向控制算法，内容包含算法原理解析，算法算法误差及应用场景对比，当前量产方案，未来趋势。自动驾驶系统中控制模块包含横向控制和纵向控制；控制模块直接发出线控指令，控制转向系统，制动系统，传动系统，动力系统，是车辆安全的核心模块。自动驾驶系统除控制模块外通常包含以下核心模块：

1.感知（Perception）：

• 功能：通过传感器（摄像头、激光雷达、毫米波雷达、超声波雷达等）感知环境信息，包括车道线、障碍物、交通标志、行人等
• 关键技术：目标检测、语义分割、多传感器融合（Sensor Fusion）。

2.定位（Localization）：

• 功能：结合高精地图、GPS、IMU和轮速计数据，实时确定车辆在全局坐标系中的精确位置（厘米级精度）。

3.决策（Decision Making）：

• 功能：根据感知和定位信息，规划车辆的行为（如跟车、换道、停车、避障等）。
• 实现方式：基于规则的有限状态机（FSM）或强化学习（RL）模型。

3.路径规划（Path Planning）：

• 功能：生成从当前位置到目标位置的全局路径，并实时更新局部避障轨迹。
• 典型算法：A*、RRT*、Frenet坐标系轨迹优化。

4.速度规划（Speed Planning）：

• 功能：根据路径曲率、交通规则、障碍物动态，规划车辆的速度曲线（如匀速、加减速策略）。
• 实现方式：基于安全距离模型（TTC, Time-to-Collision）或优化算法。

5.横向控制（Lateral Control）：功能：控制方向盘转角，使车辆沿规划路径行驶（如车道居中、弯道跟踪）。6.纵向控制（Longitudinal Control）：功能：制油门和刹车，调节车速以保持与前车的安全距离或跟踪目标速度。控制模块是如何工作的呢？接下来进行详细讲解。纵向控制模块是通过调节油门和刹车，控制车速与车距，实现安全、平顺的纵向运动。横向控制模块是通过调整方向盘转角，控制车辆横向位置与航向角，使车辆沿着预期的轨迹行驶。横向控制是车辆是否能够按照规划轨迹行驶的关键，用于自动驾驶的横向控制算法有很多种，每种控制算法有其应用场景和发展过程，以下将对这些算法进行详细讲解和横向对比。

 

 

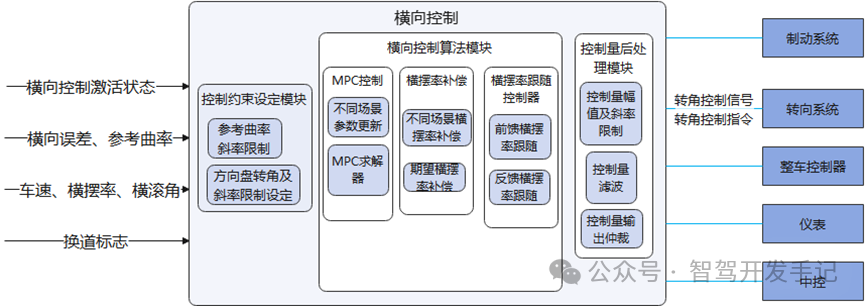
添加图片注释，不超过 140 字（可选）

二、横向控制算法分类

自动驾驶车辆横向控制算法有PID、Pure Pursuit、Stanley、Rear wheel feedback、LQR等常用的控制算法，除以上常见的横向控制算法外，自动驾驶横向控制算法还有：

• 模型预测控制（MPC）：基于车辆动态模型，通过预测未来状态并优化代价函数确定控制输入。
• 基于视觉的横向控制算法：利用摄像头图像提取车道线信息，计算横向偏差和航向偏差进行控制。
• 滑模控制（SMC）：通过设计滑模面实现鲁棒控制，适用于非线性系统。
• 模糊控制：基于模糊逻辑处理不确定性和非线性问题。 三、横向控制算法原理及实现

1.PID控制算法

1)输入：目标横向位置/航向角、实际横向位置/航向角。

2)输出：方向盘转角。

3)原理：PID控制是经典反馈控制方法，通过比例（P）、积分（I）、微分（D）环节线性组合误差信号，实现快速响应与稳态误差消除。PID实时计算目标路径与车辆实际位置的横向偏差ey和航向偏差 eθ，结合比例、积分、微分项生成控制指令。

4)核心公式：

 

 

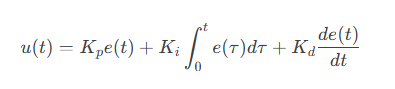
添加图片注释，不超过 140 字（可选）

参数说明：

o Kp：比例增益，决定响应速度，过高会导致振荡。

o Ki：积分增益，消除稳态误差，过高可能引发积分饱和。

o Kd：微分增益，抑制超调，对噪声敏感。

5)应用实例：

o 低速场景（<30 km/h）的园区物流车，横向误差控制在0.1-0.3 m。

o 特斯拉早期Autopilot版本在车道保持中采用PID辅助控制。

2.Pure Pursuit算法

1)输入：车辆位置、速度、预瞄距离、目标路径点。

2)输出：方向盘转角。

3)原理：Pure Pursuit是一种几何跟踪控制算法，也被称为纯跟踪控制算法。该算法最早由R.Wallance在1985年提出，其思想是基于当前车辆的后轮中心位置，在参考路径上以Ld前视距离匹配一个预瞄点，车辆以一定的角度向预瞄点行驶。是指几何路径跟踪算法，通过预瞄点计算转向角，使车辆沿圆弧轨迹逼近目标路径。算法核心在于动态调整预瞄距离 Ld，使其与车速正相关（Ld=k⋅v）。假设车辆后轮中心可以按照一定的转弯半径𝑅行驶至该预瞄点，然后根据前视距离𝑙𝑑、转弯半径𝑅、车辆坐标系下预瞄点的朝向角𝛼之间的几何关系来计算前轮转角𝛿。

 

 

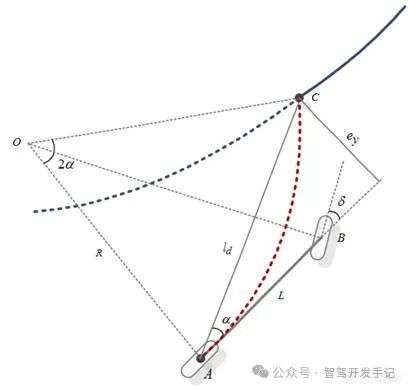
添加图片注释，不超过 140 字（可选）

如上图所示，在三角形OAC中，根据正弦定理可得

 

 

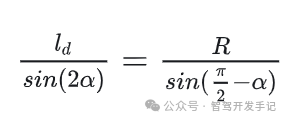
添加图片注释，不超过 140 字（可选）

根据车辆运动学方程可得：

 

 

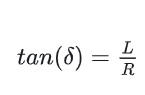
添加图片注释，不超过 140 字（可选）

所以前轮转角为：

 

 

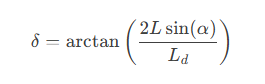
添加图片注释，不超过 140 字（可选）

定义横向误差为后轮中心位置和预瞄点在横向上的误差，如上图中的ey

 

 

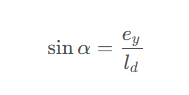
添加图片注释，不超过 140 字（可选）

由以上公示可计算前轮转角：

 

添加图片注释，不超过 140 字（可选）

根据三小函数小角度近似可得：

 

 

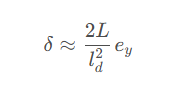
添加图片注释，不超过 140 字（可选）

在pure pursuit方法中，ld可用自动驾驶车辆纵向线速度表示为：ld=λVx+c，（c为常数）。把2L/（l2d）看作比例控制器的参数，ey是系统误差，那么这就相当于一个以横向跟踪误差CTE作为系统误差的比例控制器。

参数说明：

o L：车辆轴距（m），决定车辆转弯半径。

o α：车辆航向与预瞄点连线的夹角（rad）。

o Ld：预瞄距离（m），通常取车速的1.5-2倍时间常数。

o ey横向误差。

4)应用实例：

o 农业机械自动驾驶（如John Deere收割机），横向误差0.2-0.5 m。

o 无人驾驶赛车Indy Autonomous Challenge中路径跟踪。

3.Stanley算法

1)输入：车辆位置、速度、航向角、目标路径点。

2)输出：方向盘转角。

3)原理：Stanley算法是非线性反馈控制，综合横向偏差和航向偏差生成转向指令。该算法是Stanford团队为DARPA挑战赛设计的算法，引入航向偏差修正项和速度相关横向偏差补偿项。

Stanley 算法是一种基于几何路径的轨迹追踪控制器，其设计理念是将参考点设置在前轮中心，而非传统的重心、质心或后轮重心，所以Stanley算法又称为Front wheel feedback算法。这种设计方式使得该算法能够在路径追踪过程中实现全局收敛，并且误差衰减速率不随车辆速度变化而改变。实验结果表明，以前轮中心为参考点的控制器性能优于以重心或后轮重心为参考点的控制器。

 

 

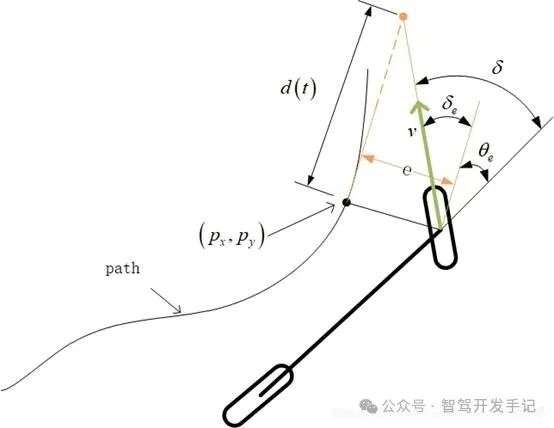
添加图片注释，不超过 140 字（可选）

根据车辆位姿与给定路径的相对几何关系可以直观的获得控制车辆方向盘转角的控制变量，其中包含横向偏差e和航向偏差θe 。

 

 

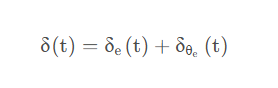
添加图片注释，不超过 140 字（可选）

在不考虑横向跟踪误差的情况下，前轮偏角和给定路径切线方向一致，如图所示。其中θe表示车辆航向与最近路径点切线方向之间的夹角，在没有任何横向误差的情况下，前轮方向与所在路径点的方向相同：

 

 

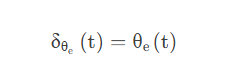
添加图片注释，不超过 140 字（可选）

在不考虑航向跟踪偏差的情况下，横向跟踪误差越大，前轮转向角越大，假设车辆预期轨迹在距离前轮d (t)处与给定路径上最近点切线相交，根据几何关系得出如下非线性比例函数：

 

 

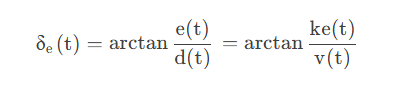
添加图片注释，不超过 140 字（可选）

其中d(t)与车速相关，最后用车速v(t)，增益参数k表示。随着横向误差的增加， arctan函数产生一个直接指向期望路径的前轮偏角，并且收敛受车速v(t)限制。

综合两方面控制因素，基本转向角控制率如下：

 

 

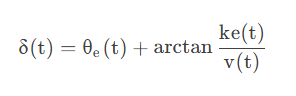
添加图片注释，不超过 140 字（可选）

使用线性自行车运动模型，可以得到横向误差的变化率：

 

 

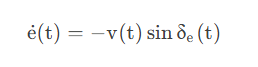
添加图片注释，不超过 140 字（可选）

其中sinδe(t)根据几何关系可知：

 

 

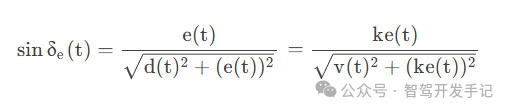
添加图片注释，不超过 140 字（可选）

所以可得：

 

 

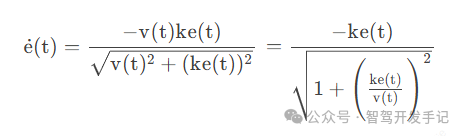
添加图片注释，不超过 140 字（可选）

当横向跟踪误差e(t)很小时， (ke(t)/v(t)) 2→0:

 

 

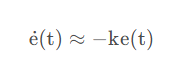
添加图片注释，不超过 140 字（可选）

通过积分上式:

 

 

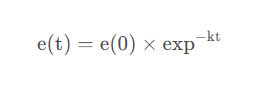
添加图片注释，不超过 140 字（可选）

因此横向误差指数收敛于e(t)=0，参数k决定了收敛速度。对于任意横向误差，微分方程都单调的收敛到0。

o 航向偏差修正：直接调整车辆航向与路径切线对齐。

o 横向偏差补偿：低速时增大转向响应，高速时平滑过渡。

参数说明：

o θe：航向偏差（rad），路径切线与车辆航向的夹角。

o e：横向偏差（m），车辆质心到路径的垂直距离。

o k：增益系数，通常取0.1-0.3。

4)应用实例：

o 大众ID.4的L2级车道居中功能（横向误差<0.15 m）。

o 低速无人配送车在复杂城市道路的路径跟踪。

4.Rear Wheel Feedback算法

1)输入：后轮位置、速度、目标路径。

2)输出：方向盘转角。

3)原理：基于后轮位置反馈，通过运动学模型计算前轮转角。假设后轮严格沿路径运动，以前轮转向角为控制量，通过后轮位置偏差设计反馈控制器：

• 计算后轮到路径的横向偏差 erer。
• 根据车辆运动学模型推导前轮转角与 erer的关系。

4)核心公式：

 

 

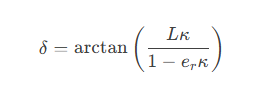
添加图片注释，不超过 140 字（可选）

参数说明：

• κ：路径曲率（m⁻¹），由路径规划模块提供。
• er：后轮横向偏差（m）。

5)应用实例：

• 港口AGV集装箱运输车（横向误差0.3-0.6 m）。
• 叉车自动化改造中的低成本方案。

5.LQR算法

1)输入：车辆状态变量（位置、速度、航向角）、目标状态。

2)输出：方向盘转角。

3)原理：LQR是基于线性二次型最优控制理论，设计状态反馈增益矩阵。将车辆横向动力学建模为线性状态空间方程，通过求解Riccati方程最小化代价函数实现最优控制的方法。

 

 

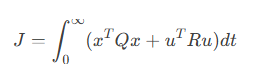
添加图片注释，不超过 140 字（可选）

o 状态变量 x：横向偏差、航向偏差及其导数。

o 控制输入 u：前轮转角或方向盘转角。

4)核心公式：

 

 

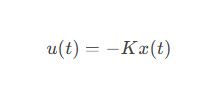
添加图片注释，不超过 140 字（可选）

5)参数说明：

o Q：状态权重矩阵，决定跟踪精度优先级。

o R：控制输入权重矩阵，限制转向剧烈程度。

6)应用实例：

o 丰田TSS 3.0高速公路车道保持（横向误差<0.1 m）。

o 无人机地面跟随车辆的横向控制。

6.MPC算法

1)输入：车辆状态、预测时域路径、动力学模型参数。

2)输出：方向盘转角。

3)原理：MPC是运用滚动时域优化，结合动力学约束与多目标代价函数的控制方法。在每个控制周期内，基于车辆非线性模型预测未来 N步的状态轨迹，求解以下优化问题：

 

 

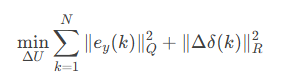
添加图片注释，不超过 140 字（可选）

o 约束条件：转向角速率限制、轮胎摩擦圆等。

4)核心公式：

 

 

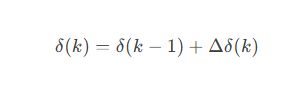
添加图片注释，不超过 140 字（可选）

参数说明：

o N：预测时域（通常5-20步，对应1-5秒）。

o Q,R：误差与控制增量的权重。

5)应用实例：

o 奔驰DRIVE PILOT高速NOA功能（横向误差<0.05 m）。

o 复杂交叉路口无保护左转场景控制。

7.基于视觉的横向控制算法

1)输入：摄像头图像、车道线模型。

2)输出：方向盘转角。

3)原理：通过视觉感知直接生成控制指令，实现端到端横向控制。：

o 图像处理：使用CNN提取车道线特征，输出横向偏差 ey 和航向偏差 eθ。

o 控制映射：通过PID或模糊逻辑将偏差映射为方向盘转角。

4)核心公式：

 

 

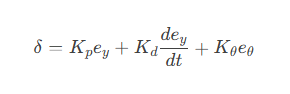
添加图片注释，不超过 140 字（可选）

参数说明：

o Kp，Kd，Kθ：视觉偏差的PID增益。

5)应用实例：

o Mobileye EyeQ4芯片的车道居中功能（横向误差0.1-0.2 m）。

o 特斯拉FSD Beta城市道路无高精地图控制。

四、算法对比与分析

对比维度	PID	Pure Pursuit	Stanley	RearWheelFeedback	LQR	MPC	基于视觉
鲁棒性	中等	低	中等	低	高	高	中等
横向位置误（m）	0.1-0.3（低速）	0.2-0.5	0.05-0.15	0.1-0.3	0.05-0.1	0.02-0.08	0.1-0.3
航向误差	1.5-3.0	2.0-5.0	0.5-1.5	1.5-3.0	0.3-1.0	0.2-0.8	1.0-2.5
路径要求	无	需全局路径	需局部路径	需路径	需路径	需路径	需车道线
超调量	高	中等	低	低	低	低	中等
典型场景	1.停车场泊车 2.低速园区车 3. 简单车道保持	1.农业机械 2.结构化道路 3.中低速跟踪	1.城市复杂路况 2.动态避障 3.高速弯道	低速跟踪	1.高速公路巡航 2.稳定跟车 3.换道控制	1. 动态障碍物场景 2. 极限工况 3. 多目标优化	1.车道保持 2.无地图导航 3.视觉SLAM融合

五、量产方案与未来趋势

1.当前量产NOA方案

当前乘用车量产的NOA（Navigate on Autopilot）方案中，横向控制多采用MPC与LQR结合的优化算法，辅以基于视觉的横向偏差补偿（如特斯拉FSD的“混合控制策略”）。MPC因其对动态环境和多约束的处理能力，成为高速场景下的主流选择。

2.量产车型横向误差的实际表现

• 主流误差范围： 当前量产乘用车的横向控制误差通常控制在 10–30 cm 范围内。例如：
• 低速场景（<30 km/h）：误差可控制在 5–15 cm（如停车场自动泊车）。
• 高速场景（>80 km/h）：误差增大至 15–30 cm，受侧风、路面摩擦系数变化等因素影响显著。
• 典型量产方案案例：
• 主流方案：L4级以下车型（如小鹏NGP、蔚来NOP）普遍采用MPC为主 + LQR修正的混合架构，理想横向误差≤0.1 m；实际误差高速直道误差约10–20 cm，复杂弯道误差达20–35 cm。
• 视觉增强：特斯拉FSD通过8摄像头融合BEV模型，实现无高精地图的横向控制（误差0.15-0.3 m），其中在高速车道保持中横向误差约10–25 cm，弯道误差可能超过30 cm。

3.理论误差与实际误差的差异原因

理论模型的局限性：

• 算法（如Stanley、LQR）的理论推导通常基于简化运动学模型，假设车辆为刚体且忽略轮胎侧偏、悬架动态等非线性因素。
• 例如，Stanley算法的指数收敛性（e(t)=e(0)⋅e−kte(t)=e(0)⋅e−kt）仅在理想条件下成立。

实际干扰因素：

• 传感器噪声：摄像头、激光雷达的感知误差（±5 cm）直接影响横向偏差计算。
• 执行器延迟：方向盘转向系统的机械响应延迟（约100–300 ms）导致控制指令滞后。
• 环境扰动：侧风、路面坡度变化等可引入额外横向偏移（高速时可达10–20 cm）。

4.量产算法的优化策略与误差控制

多传感器融合：

• 结合视觉车道线识别（误差±10 cm）与高精地图（误差±5 cm），通过卡尔曼滤波降低综合感知误差。

动态参数调整：

• 车速自适应：如Stanley算法中预瞄距离Ld=k⋅vLd=k⋅v，避免高速时转向不足。
• 曲率补偿：针对弯道离心力，MPC算法增加路径曲率前馈项，减少轨迹跟踪超调。

鲁棒性增强：

• 死区处理：在直道工况下设置方向盘转角死区（±2°），抑制微小抖动导致的误差波动。
• 零漂修正：通过实时识别方向盘零位偏差（如±5°），动态调整控制指指令。

5.未来趋势与误差改进方向

• 端到端学习控制： 如Waymo的ChauffeurNet，通过深度学习直接映射感知数据到转向指令，减少模型简化带来的误差（目标误差<10 cm）。 高精度执行器：采用线控转向系统（响应延迟<50 ms），提升控制实时性。 V2X协同控制：通过车路协同获取全局路径信息，减少局部规划累积误差。
•  

总结

理论算法（如Stanley、LQR）的横向误差收敛性在理想条件下成立，但实际量产中受传感器、执行器和环境干扰的影响，误差显著增大。当前主流量产方案的横向误差在 10–30 cm 之间，未来通过多模态感知融合与执行器优化，有望将误差进一步压缩至 5–15 cm 以内。

 

参考文献链接

八种量产自动驾驶横向控制算法PID、Pure Pursuit、Stanley、LQR、MPC、RearWheelFk详解及对比