全局平衡二叉树

非常好，学习一下科技，这下可以爆踩树剖

全局平衡二叉树

性质

全局平衡二叉树是一种可以处理树上链修改/查询的数据结构，可以做到：

• \(O(\log n)\) 一条链整体修改
• \(O(\log n)\) 一条链整体查询

还可以 \(O(\log n)\) 求最近公共祖先，子树修改，子树查询等，这些复杂度和重链剖分是一样的。

全局平衡二叉树的主要性质如下：

1. 它由很多棵二叉树通过轻边连起来组成，每一棵二叉树维护了原树的一条重链，其中序遍历的顺序就是这条重链深度单调递增的顺序。每个节点都仅出现在一棵二叉树中。
2. 边分为重边和轻边，重边是包含在二叉树中的边，维护的时候就像正常维护二叉树一样，记录左右儿子和父节点。轻边从一颗二叉树的根节点指向它所对应的重链顶端节点的父节点。轻边维护的时候“认父不认子”，即只能从子节点访问到父节点，不能反过来。注意，全局平衡二叉树中的边和原树中的边没有对应关系。
3. 算上重边和轻边，这棵树的高度是 \(O(\log n)\) 级别的。这条是保证复杂度的性质。

第一张图是原树，以节点 \(1\) 为根节点。第二张图是建出来的全局平衡二叉树，其中虚线是轻边，实线是重边，一棵二叉树用红圈表示。

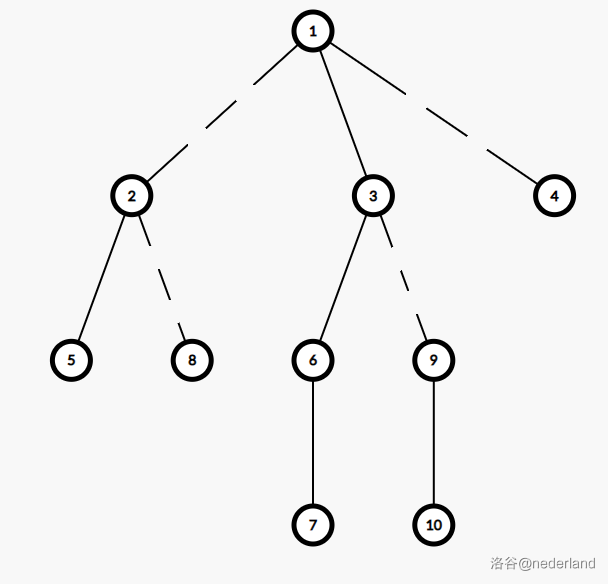
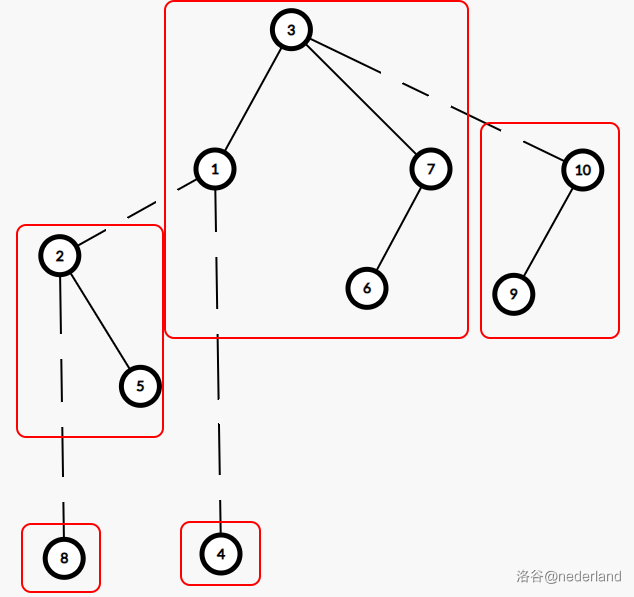
建树

首先是像普通重链剖分一样，一次 dfs 求出每个节点的重儿子。然后从根开始，找到根节点所在的重链，对于这些点的轻儿子递归建树，并连上轻边。然后我们需要给重链上的点建一棵二叉树。我们先把重链上的点存到数组里，求出每个点轻儿子的 size 和 \(+1\)。然后我们按照这个求出这条重链的加权中点，把它作为二叉树的根，两边递归建树，并连上重边。

可能不是很好理解，代码如下：（这题解怎么这么喜欢do while啊？）

std::vector<int> G[N];
int n, fa[N], son[N], siz[N];
void dfsS(int u) {
	siz[u] = 1;
	for (int v : G[u]) {
		dfsS(v);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]]) son[u] = v;
	}
}
int b[N], sum[N], l[N], r[N], f[N], ss[N];
// 给b中[bl,br)内的点建二叉树，返回二叉树的根
int cbuild(int bl, int br){
	int l=bl,r=br,mid,ans;
	while(l<=r){
		int mid=(l+r)>>1;
		if (2*(sum[mid]-sum[bl])<=sum[br]-sum[bl]) l=mid+1,ans=mid;
		else r=mid-1;
	}
	// 二分求出按sum加权的中点。不使用二分而是直接扫一遍复杂度也对
	int rt=b[ans];
	siz1[rt]=br-bl+1; // ss：二叉树中重子树的大小
	if(ans>bl){
        l[y]=cbuild(bl, x);
        fa[l[y]]=y;
    }if(ans<br){
        r[y]=cbuild(x+1, br);
        fa[r[y]]=y;
    }
	return rt;
}
int build(int x){
	int y=x;
    for(;y;y=son[y]){
        for4(to,v[y])
		if(to!=son[y]) fa[build(v)]=y;
    }//就是按照重儿子遍历下去
    //递归建树并连轻边，注意要从二叉树的根连边，不是从儿子连边
	y=0;
    for(;x;x=son[x]){
        b[++y]=x;
        sum[y]=sum[y-1]+siz[x]-siz[son[x]]
    }
	return cbuild(0, y);
}

由代码可以看出建树的时间复杂度是 \(O(n\log n)\)。首先我们cbuild就是\(O(n\log n)\)的，因为，我们每次递归下去siz都会/2，然后每个点最多进一次cbuild，然后就好了。

接下来我们可以证明树高是 \(O(\log n)\) 的：考虑从任意一个点跳父节点到根。由重链剖分的性质可得跳轻边最多 \(O(\log n)\) 条；因为cbuild每次递归下去siz都会/2，所以二叉树高度不超过 \(O(\log n)\)，所以跳重边最多也是 \(O(\log n)\) 条。整体树高就是 \(O(\log n)\) 的。

修改

每一棵二叉树维护了原树的一条重链，其中序遍历的顺序就是这条重链深度单调递增的顺序。每个节点都仅出现在一棵二叉树中。

链修改:
每一棵二叉树维护了原树的一条重链，其中序遍历的顺序就是这条重链深度单调递增的顺序。每个节点都仅出现在一棵二叉树中。
观察一下一条链在一颗二叉树上的呈现情况，那么我们一条链肯定是一个二叉树的一个联通块，我们直接维护子树和，因为树高最多为log，然后就可以了。这个要标记永久化。

怎么说呢，这个东西实现一些区间和还是比较简单的，但是万一是什么赋值什么的我也不太会了，这个还是很神秘的

然后就好了。

[P4751]
全局平衡二叉树就是为了这个！
这题是单点修改矩阵，然后整个链查询。比如我们修改了一个点，然后我们这个点到根进行加。我们要快速完成二叉树的剖掉一个子树的求和。我们改一个点的时候只会影响到二叉树的\(log\)个点，所以我们不停往上跳，像平衡树那样push_up即可

然后有点忘记掉ddp了，复习一下。
设\(dp[u][0/1]\)为这个点选/不选的最大代价

\(dp[u][0]=\sum max(dp[u][0],dp[u][1])\)
\(dp[u][1]=\sum dp[u][0]\)

然后我们矩阵乘法的定义是

for1(i,1,n){
    for1(j,1,n){
        for1(k,1,n){
            c[i][j]=max(c[i][j],a[i][k]+b[k][j])
        }
    }
}

或者我们还是要像重链剖分一样维护轻儿子和重儿子。那么我们维护的时候就还是这么搞，最下面那个二叉平衡树一个\(sum\)，每次跳一个轻链就乘以下，然后再乘以下\(sum\)的矩阵，然后就做完了。是吗，让我想想，对的对的

所以感觉全局平衡二叉树的本质就是把每条重链重构成一个二叉树。

那么我们修改一个点的矩阵时就向上更新\(sum\)，矩阵的结合律确实要考虑一下。然后更新链顶。怎么更新呢？也很简单，减掉原来的，再加上后面的。

想想矩阵
\(f[u][0]=max(f[son[u]][0]+g[u][1],f[son[u]][1]+g[u][1])\)$

\(f[u][1]=f[son[u]][0]+g[u][0]+a[u]\)

然后还有一些边边角角，叶子的矩阵是dp方程

f[son[u][0]] f[son[u][1]]
-1e9 -1e9

g[u][1] g[u][0]+a[u]
g[u][1] -1e9

然后发现写了一坨自己不是特别熟悉的东西，向题解学习，发现可以重构成平衡树

有一个比较神奇的地方就是重构二叉树的时候我们的\(siz\)是\(siz[x]-siz[son[x]]\)，然后我们再重构

然后就比较搞笑了，这个矩阵乱乘，然后按道理边界不会有问题啊？

为什么啊！为什么要从后往前乘啊？
我以前ddp不是从前往后的吗？

首先，我们的dp方程是放在后面的，所以啊！