关于dfs序求lca的一点思考

最近学了一点黑科技，这就是一个。有一个结论

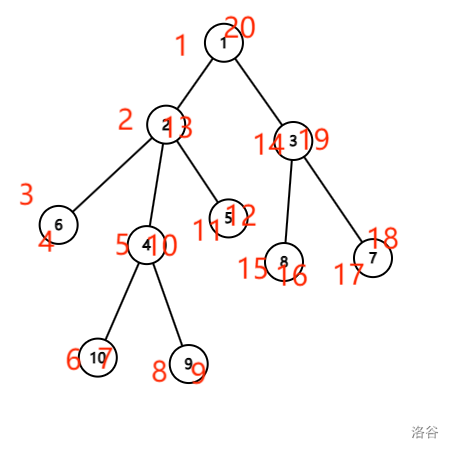
比如这就是一个\(dfn\)序。在代码中，常常对\(beg\)和\(ed\)都开一个数组。如果一个点是\(x,y\)的\(lca\)记为\(g\)，那么有以下结论\(beg[g]<min(beg[x],beg[y]),ed[g]>max(ed[x],ed[y])\)
感性理解即可。所以我们就可以在符合的点找深度最大的。这是一种思路，常常是用来压缩多次\(lca\)的，如P7103。然后这还有个\(O(n \log n)-O(1)\)求lca的做法。是在beg[x]和ed[y]中找深度最小的节点，他的父亲就是\(lca\)。比如图中\(6,5\)的\(lca,dfn\)中\(3-12\)中有\(6,4,10,9,5\)这几个节点，用\(rmq\)维护一下就可以了

然后学了\(dfs\)序的\(lca\)，现在总该会了吧。我们看看\(dfn[x]\)到\(dfn[y]\)的节点到底是哪些，是\(x\)往下走的节点，直到走到\(y\)，那么一定走到一个节点使得其为\(lca\)的\(son\)，对于\(x\)为\(y\)祖先，只需将查询区间变为\([dfn[x]+1,dfn[y]]\)即可