单调队列+决策单调性dp学习笔记
What Is Monotonic Queue
单调队列是一种特殊的队列数据结构,用于维护一定的单调性,通常是单调递增或单调递减。
单调队列的主要特点是,队列中的元素满足特定的单调性要求,使得队列的头部元素(或者尾部元素,取决于具体问题)始终是当前队列中的最大(或最小)值。这种特性使得单调队列可以高效地处理一些需要在不断变化的窗口或序列中找到最大(或最小)值的问题。
Monotonic Queue Can Do What
单调队列在解决一些与窗口和单调性有关的问题时非常有用。以下是一些可以使用单调队列解决的常见问题:
-
滑动窗口最大/最小值: 给定一个数组和一个固定大小的窗口,需要在窗口在数组上滑动的过程中,快速找到每个窗口的最大或最小值。
-
连续子数组的平均值大于阈值的个数: 给定一个数组和一个阈值,找到所有长度为固定值的连续子数组,使得子数组的平均值大于给定的阈值。
-
下一个更大元素: 给定一个数组,对于每个元素,找到在其右边第一个比它大的元素。
这些问题在实际应用中非常常见,而单调队列可以帮助有效解决这些问题,因为它们可以在\(O(n)\)的时间复杂度内进行操作,而不是传统的\(O(n^{2})\)解法。通过维护单调性,单调队列可以在滑动窗口或者数组遍历的过程中高效地找到满足特定条件的元素。
How To Solve These Question
1.滑动窗口最大/最小值
例题:- P1886 滑动窗口 /【模板】单调队列
这题之前使用线段树做的,但是\(nlogn>n\),1.55s>1.33s。用单调队列整整快了0.22s也不是很多。
当使用单调队列来解决滑动窗口最大/最小值问题时,需要维护一个滑动窗口,以及一个单调递减队列。单调队列用于存储当前窗口内的元素的下标(因为要保持单调队列元素在窗口内),使得队列的头部始终是窗口内的最值元素。以下是解决滑动窗口最大值问题的方法:
假设有一个数组 \(arr\) 和一个窗口大小 k,我们需要找到每个窗口的最大值。
创建一个单调递减队列 deque,用于存储元素在窗口中的下标。
遍历数组,对于每个元素 \(i\) 进行以下操作:
在每个新元素要加入窗口时,从队列尾部开始,将所有比新元素小的元素下标出队,以保持队列的单调递减性质。
将当前元素下标入队到队列尾部。
对于每个窗口的起始位置,计算窗口内的最大值并记录。
#include<bits/stdc++.h>
using namespace std;
long long n,k,a[1000005];
deque<int>q;//双端队列
int main(){
cin>>n>>k;
for(long long i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
while(!q.empty()&&q.front()<i-k+1){//保证元素在窗口内
q.pop_front();
}
while(!q.empty()&&a[i]<=a[q.back()]){//保证队列内单调递增(队首为区间最小值)
q.pop_back();
}
q.push_back(i);
if(i>=k) cout<<a[q.front()]<<" ";
}
cout<<endl;
while(!q.empty()){//同上
q.pop_front();
}
for(int i=1;i<=n;i++){
while(!q.empty()&&q.front()<i-k+1){
q.pop_front();
}
while(!q.empty()&&a[i]>=a[q.back()]) {
q.pop_back();
}
q.push_back(i);
if(i>=k) cout<<a[q.front()]<<" ";
}
return 0;
}
2.连续子数组的平均值大于阈值的个数
Leetcode 1343
本人没有leetcode账号qwq,只能看题面了
因为滑动窗口长度为\(k\),所以用双端队列即可
#include<bits/stdc++.h>
using namespace std;
int n,a[1000005],k,t,sum=0,ans=0;
deque<int>q;
int main(){
cin>>n>>k>>t;
t=k*t;//平均值>=t -> 子数组数的和>=k*t
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
while(!q.empty()&&q.front()<i-k+1){//超出范围就pop
sum-=a[q.front()];
q.pop_front();
}
q.push_back(i);
sum+=a[i];
if(sum>=t) ans++;//看看可不可以
}
cout<<ans<<endl;
return 0;
}
3.下一个更大元素
例题: P1901 发射站
XJOI上 \(n^{2}\) 过百万
假设我们有一个数组 arr,我们要为每个元素找到在其右边第一个比它大的元素。我们可以使用一个单调递减队列来解决这个问题。队列中的元素按照从大到小的顺序排列,当我们遍历数组时,如果当前元素大于队列末尾的元素,那么我们就可以得到队列末尾元素的下一个更大元素。
1.创建一个空的 deque
遍历数组,对于每个元素执行以下操作:
如果队列不为空,并且当前元素大于等于队列末尾的元素,那么说明队列末尾的元素找到了下一个更大元素。我们将队列末尾的元素弹出,并将其下标与当前元素建立映射,表示下一个更大元素的位置。
将当前元素的下标入队到队列中,以便稍后可以根据下标获取元素。
遍历完成后,队列中剩余的元素表示没有找到下一个更大元素的位置,可以标记为 -1 或数组长度。
#include<bits/stdc++.h>
using namespace std;
long long n,h[1000005],v[1000005],ans[1000005];
void getmax() {
stack<long long>stk;//单调栈
for (long long i=1;i<=n;i++){//对于每一个i进行操作
while(!stk.empty()){
if(h[i]<=h[stk.top()]) break;//不符合要求
long long j=stk.top();
if(!stk.empty()){
ans[i]+=v[j];//h[j]<h[i] -> j向i发射
}
stk.pop();
}
if(!stk.empty()) ans[stk.top()]+=v[i];//没有别的高就是i向stk.top()发射
stk.push(i);
}
}
int main(){
cin>>n;
for(long long i=1;i<=n;i++){
cin>>h[i]>>v[i];
}
getmax();
long long maxx=-1;
for(long long i=1;i<=n;i++){
maxx=max(maxx,ans[i]);
}
cout<<maxx<<endl;
return 0;
}
4.决策单调性
单调队列
例题:最大子串和
很简单想到一个\(O(n \log n)\)类似线段树的做法(学ds学的)
然而这个显然可以先求一个前缀和,然后对于每一位在前面找到一个最小的前缀和,然后取\(max\)即可,这是\(O(n)\)的
但如果子串长度不能超过呢?在\([r-m+1,r]\)取\(min\)有不有让你想起什么?滑动窗口,没错,就是单调队列,然后就很简单了
q.push_back(0); //因为是前缀和,可以减去s[0]
for(int i=1;i<=n;i++){
while((!q.empty())&&(i-q.front()>m)) q.pop_front();//因为是前缀和,所以是(i-q.front()>m)
ans=max(ans,s[i]-s[q.front()]);
while((!q.empty())&&(s[q.back()]>=s[i])) q.pop_back();
q.push_back(i);
}
POJ 1821
以后看到可以用dp做的题目就硬着头皮做下去,一般都是可以靠优化通过的。
一开始的dp方程(要按照这个规范写dp)
for(int i=1;i<=m;i++){
for(int j=0;j<=n+1;j++) dp[i][j]=dp[i-1][j];
for(int r=a[i].s;r<=min(n,a[i].s+a[i].l-1);r++){
for(int l=max(1,r-a[i].l+1)-1;l<=a[i].s-1;l++){
dp[i][r]=max(dp[i][r],dp[i-1][l]+a[i].p*(r-l+1));
}
}
}
然后发现最内层循环是一段范围,容易想到线段树
for(int i=1;i<=m;i++){
build(0,n,1,i);
for(int j=0;j<=n+1;j++) dp[i][j]=dp[i-1][j];
for(int r=a[i].s;r<=min(n,a[i].s+a[i].l-1);r++){
dp[i][r]=max(dp[i][r],getmax(0,n,1,max(1,r-a[i].l+1)-1,a[i].s-1)+a[i].p*r);
}
}
然后就可以了
最后放下单调队列,感觉单调队列可以被一些多一只log的ds给搞掉,这些带log的ds我还是比较熟练的。但单调队列也不是不会,放在这边吧(有点大)
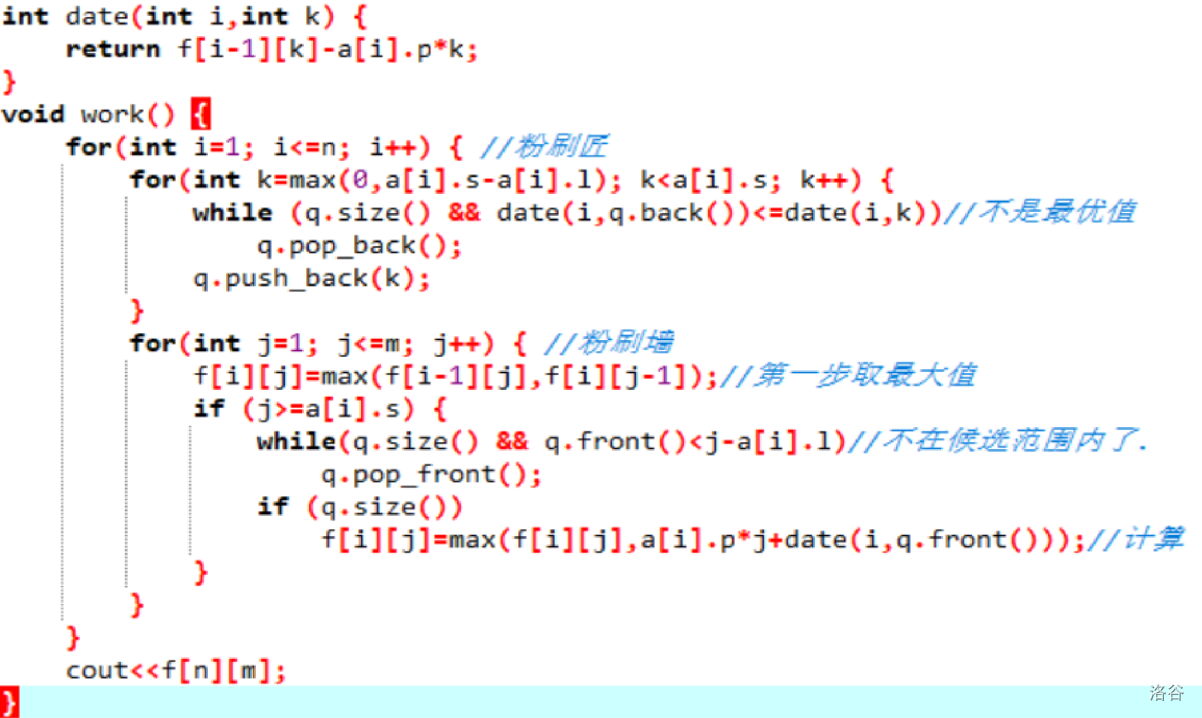
非常好的单调队列优化多重背包
总结:
\(F[i]=min/max{c(i)+d(j)+K}\) 是可用单调队列优化的基本条件,\(c(i)\) 关于 \(i\) 的多项式,\(d(j)\) 同理,\(K\) 常数
斜率优化是单调队列优化的推广
我们知道,有些 \(DP\) 方程可以转化成 \(DP[i]=f[j]+x[i]\) 的形式,其中 \(f[j]\) 中保存了只与 \(j\) 相关的量。这样的 \(DP\) 方程我们可以用单调队列进行优化,从而使得 \(O(n^{2})\) 的复杂度降到 \(O(n)\)。
具体来说就是枚举 \(i\),然后使用单调队列找到i的最优决策点 \(j\),然后就可以了。
那我们要如何处理我们的 \(dp\) 式子呢。斜率优化和单调队列都是处理 \(min/max\) 的,所以我们要枚举 \(i\),将式子全部拆开,整理成 \(F[i]=min/max(c(i)+d(j)+K)\) 再把里面常数拎出来 \(F[i]={(单调队列)d(j)}+c(i)+K\) 的样子。
斜率优化
如果 \(F[i]=min{c(i)+d(j)+e(i,j)+K}\),如何进行优化?
邦邦的ppt还是烂了
从POJ1180任务安排的解法二开始
for(int i=2;i<=n;i++){
for(int j=1;j<i;j++){
dp[i]=min(dp[i],dp[j]+sumt[i]*(sumw[i]-sumw[j])+s*(sumw[n]-sumw[j]));
}
}
按照上面单调队列的方式优化
\(dp[i]=min(dp[j]+sumt[i]*sumw[i]-sumt[i]*sumw[j]+s*sumw[n]-s*sumw[j]);\)//拆括号
\(dp[i]=min(dp[j]-sumw[j]*(sumt[i]+s))+sumt[i]*sumw[i]+s*sumw[n]\)//常数拎出
\(dp[j]=dp[i]+sumw[j]*(sumt[i]+s)-sumt[i]*sumw[i]-s*sumw[n]\)//拆掉min (与j相关的项放左边)
\(dp[j]=dp[i]+sumw[j]*(sumt[i]+s)\)//丢掉常数
看ppt,非常清楚(我原来的理解全部假了,很搞笑)
然后因为斜率是 \((sumt[i]+s)\) 所以一定是从左往右做单调队列
具体实现这篇题解也很清楚
而很多题解没讲到的一点是为了去除 \(/\) 号,都选择了移项。而因为 \(sumw[i]\) 单增,直接移项即可
放下我自己的理解吧,因为我的每一个点都是 \((sumw[j],dp[j])\) 而 \(dp[j]\) 和 \(sumw[j]\) 都是单增的,而 \((s+sumt[j])\) 也是单增的,因为我们维护的是一个凹包,所以大概就是这样子了
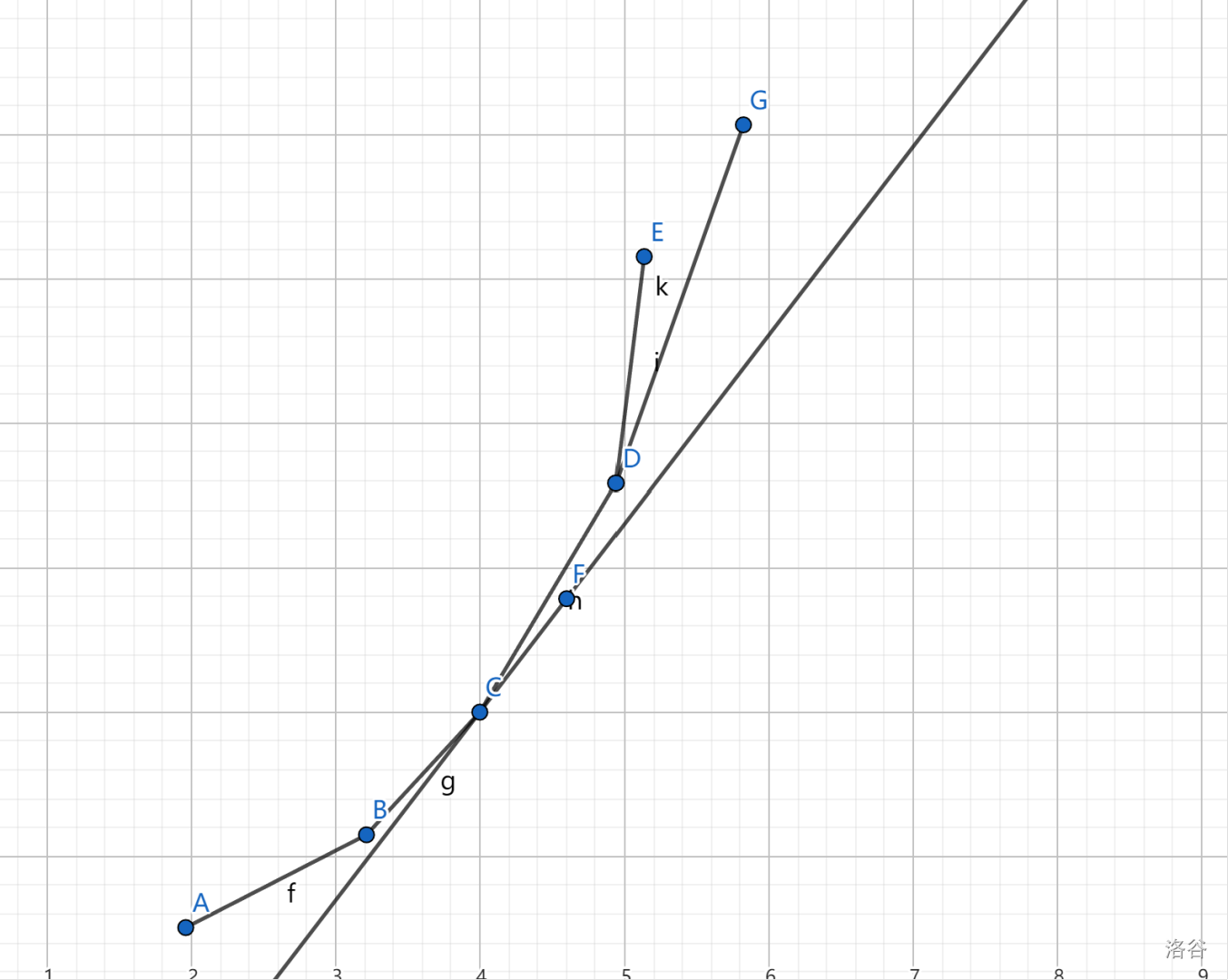
因为我们要找切线,而斜率 \((s+sumt[i])\) 是单增的,所以就从队尾删即可。而我们要维护凹包,所以从队头删,比如这个 \(E\) 点。
看加强版
破防了,在P5785 [SDOI2012] 任务安排中,\(t_{i}\) 有可能是负的,所以斜率 \((s+sumt[i])\) 不确定。所以我们就要在凹包上二分。(不二分还是有60分)
所以当我们遇到 \(0=a(i)+b(j)+c(i,j)+K\)
要处理成 \(b(j)=c(i,j)+a(i)\)(\(k\) 扔到外面了)
比如摆渡车。
容易写出 dp 方程
for(long long i=0;i<=maxx+m+1;i++){
dp[i]=i*sum[i]-sumt[sum[i]];
}
for(long long i=1;i<=maxx+m+1;i++){
for(long long j=0;j<=i-m;j++){
dp[i]=min(dp[i],dp[j]+(sum[i]-sum[j])*i-(sumt[sum[i]]-sumt[sum[j]]));
}
}
然后拆开
\(dp[i]=min(dp[i],dp[j]+sum[i]*i-sum[j]*i-sumt[sum[i]]+sumt[sum[j]])\)(拆括号)
\(dp[i]=dp[j]+sum[i]*i-sum[j]*i-sumt[sum[i]]+sumt[sum[j]]\)(拆掉min)
\(dp[i]=dp[j]-sum[j]*i+sumt[sum[j]]\)(丢掉常数)
\(dp[j]=sum[j]*i-sumt[j]+dp[i]\) 整理成一般式
然后注意在斜率优化时,我们常常会移项,这时要考虑正负性(最好是分讨一下)
double getk(int i,int j){
if(sum[i]-sum[j]==0) return (double)(dp[i]+sumt[i]-dp[j]-sumt[j])*1e9;<-------这一行要格外注意。因为两个除以0的也要比较
return (double)(dp[i]+sumt[i]-dp[j]-sumt[j])*1.0/(double)(sum[i]-sum[j]);
}
for(long long i=0;i<=maxx+m-1;i++){
if(i>=m){//如果第二层循环有范围的话就要这样写
while((r>l)&&(getk(q[r],q[r-1])>=getk(i-m,q[r-1]))) r--;
r++;
q[r]=i-m;
}
while((r>l)&&(getk(q[l+1],q[l])<=i)) l++;
if(l<=r) dp[i]=min(dp[i],dp[q[l]]+(sum[i]-sum[q[l]])*i-(sumt[i]-sumt[q[l]]));
}
四边形不等式
用来解决 \(dp[i]=\min\limits_{j=0}^{i-1} dp[i]+v[i,j]\)(可以为 \(min\) 或 \(max\))
1. 定义
如果对于二维序列 \(w\) 中任意四个整数 \(a \leq b \leq c \leq d\) 都有 \(w_{a,d} + w_{b, c} \geq w_{a, c} + w_{b, d}\),则称 \(w\) 满足足四边形不等式关系。
蒙日矩阵:满足四边形不等式的就是蒙日矩阵。四边形不等式本质是差分数组 \(\ge 0\)
2. 性质
若对于任意两个整数 \(i < i + 1 \leq j < j + 1\),都有 \(w_{i, j + 1} + w_{i + 1, j} \geq w_{i, j} + w_{i + 1, j+1}\),那么 \(w\) 满足四边形不等式。
证明:
利用差分理解即可
上述的结论通常用于证明 \(v\) 满足四边形不等式,与下文的 DP 优化关联不大。
PS:为什么叫四边形不等式?

对于任意四边形,显然有对角线的和 \(\geq\) 两对边之和,如图,\(AD+BC \geq AC+BD\)。证明方式为三角形两边之和大于第三边。
3. 优化 DP
考虑一类决策性 DP,其转移方程形如 \(f_i = \min \limits _{0 \leq j < i} \{f_j + v_{j, i}\}\)。这类转移方程通常是类似这样的题目:\(n\) 个数,要分成若干连续段,定义每一段的价值,要求最小化每段价值之和。这时我们设 \(f_i\) 表示前 \(i\) 个数分段的最小价值和,那么枚举 \(j\) 即枚举 \(i\) 属于哪一段,\(v_{j,i}\) 则是这一段的价值。
最优决策:\(f_{i}\) 转移的 \(j\)
对于这一类问题,可以使用四边形不等式。
- 性质 1
随着 \(i\) 递增,\(p_{i}\) 也递增
- 性质 2
若 \(j\) 对 \(i\) 的转移比 \(x\) 对 \(i\) 的转移优,则对于 \(i^{'}>i\),\(j\) 也比 \(x\) 优。
因为这里的 \(j\) 是任意取的,所以性质 1 是性质 2 的特殊版。而我们普通的决策单调性没有这个性质,或者说满足这个就满足了四边形不等式。
证明:
首先可以证明
由于 \(j\) 比 \(x\) 对 \(i\) 的贡献更优,所以有:\(f_j + v_{j, i} \leq f_x + v_{x, i}\)。因为 \(v\) 满足四边形不等式关系,则有 \(v_{x, i^\prime} + v_{j, i} \geq v_{x, i} + v_{j, i^\prime}\),移项变为 \(v_{j, i^\prime} - v_{j, i} \leq v_{x, i^\prime} - v_{x, i}\)。
将最后一个不等式和第一个不等式相加,有 \(f_j + v_{j, i^\prime} \leq f_x + v_{x, i^\prime}\)。
证毕。
如何优化 DP
我们可以设初始时每个 \(i\) 的决策点都为 \(0\),然后从前往后,依次用决策点算出 \(f_i\) 并尝试用 \(i\) 作为新的决策点更改其他点。
由于上面的性质成立,所以如果 \(f_i\) 可以更新 \(f_x\),那么一定可以更新 \(f_{x+1}\) 到 \(f_n\)。所以 \(f_i\) 能更新的点一定是末尾一段。假设能更新的是 \(p \sim n\),我们的目标就是找到 \(p\)。容易发现是可以二分的。
我们考虑维护一个队列,每个点维护三个数 \(l,r,c\),表示 \(l \sim r\) 每个点的当前最优决策都为 \(c\)。这个队列是对于 \(c\) 的单调队列(也就是说这个 \(c\) 是单调递增的,这个 \(l\sim r\) 组成了 \([l+1,n]\))。
我们对于 \(i\),先从后往前找到 \(p\) 所在的 \(l,r,c\),在这个过程中把必然不优的给移除出双端队列。然后在挑出 while 的 \([l,r]\) 中二分 \(p\) 的位置并更新队列即可。
当然也有一些其他实现方法,例如分治维护,复杂度也是 \(O(n \log n)\),当然分治维护实用性貌似没这么好?
特别注意:
上文的做法对于四边形不等式是正确的,但对于普通的决策单调性是错误的。
对于普通的决策单调性 DP,只能保证最终的决策点是单调的,换句话说,只能保证性质 \(1\) 成立而不能保证性质 \(2\) 成立。
我们在维护单调队列进行更新的部分时,不能保证能找到 \(p\)。\(f_i\) 能更新的不一定是末尾一段。
所以可以看出,四边形不等式得到的结论强于决策单调性的。
注意,四边形不等式是证明 \(p\) 单调性的一种充分不必要方式。即证明 \(v\) 满足四边形不等式可以推出 \(p\) 单调,但 \(p\) 单调不一定要求 \(v\) 满足四边形不等式。
可能会有小朋友问为什么不可以这样写
int q[100005],l=1,r=0;
for1(i,1,n){
while(l<r&&dp[q[l]]+calc(q[l],i)>dp[q[l+1]]+calc(q[l+1],i)) l++;
dp[i]=dp[q[l]]+calc(q[l],i);
q[++r]=i;
}
意思就是队首就是最优决策点,但是!我们的 \(dp[q[l]]+calc(q[l],i)\) 并不是单调的,可能我们做完之后最优决策点还在后面,这个我们只能 \(O(n)\) 枚举了。所以这就是我们斜率优化和四边形不等式的意义了。
例题
P3195 [HNOI2008]玩具装箱
\(ans=\sum (j-i+sum[i]-sum[j-1]-L)^{2}\)
打表证明四边形不等式
P3515
我们考虑顺序做一遍,倒序做一遍来解决前后问题
dp[i]=max(h[j]+\sqrt{i-j})-h[i]
注意到这题非常逆天,这个dp都不用求,只是要求这个最大值。重新思考一下。还是正常决策单调性吧,这题是不是不符合四边形不等式
QOJ9737
考虑dp。dp[i]=min(dp[j]+v[sum[i]-sum[j-1]]-c)
考虑决策单调性,注意到b单调不降,
二分栈,直接四边形不等式即可
UOJ852
我们还是dp,我们dp[i]为交换元素只在1~i范围内交换次数最少
dp[i]=dp[j]+v[i+1][j],首先需要i+1~j AB相等。然后我们贪心解决里面的问题即可。具体来说,我们split出里面所有的B,然后我们减一下它的相对位置即可。对于A同理。这个我们前缀和即可。然后我们就得到了\(n^{2}\) 的做法。这个前缀和显然可以 \(O(n)\) 处理,考虑后面的决策单调性,一点也没有。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号