二叉树

一、二叉树的定义

二叉树是一种树型结构，特点是每个结点至多只有两棵子树，并且有左右子树之分，次序不能颠倒。

二、二叉树性质

性质一： 在二叉树第i层上至多只有2ⁿ(i-1)个结点

性质二：深度为k的二叉树至多有2ⁿ(k)-1个结点

性质三：对任何一棵二叉树T如果其终端结点数为n0,度为2的结点数为n2,则，n0=n2+1

性质四：具有n个结点的完全二叉树的深度为└㏒2n┘+1

满二叉树：每一层结点数都是最大结点数

完全二叉树：对结点按照从上到下，从左到右编号，当且仅当每一个结点都与满二叉树编号相同

 三、二叉树存储结构

1、顺序存储

#define MAXSIZE 100
typedef TElemType SqBiTree[MAXSIZE];
SqBiTree bt;

2、链式存储结构

typedef struct BiTNode{
    TElemType data;
    struct BiNode *lchild,*rchild;//左右孩子指针
}BiTNode *Bitree;

 四、二叉树的建立和应用

 

#include<iostream.h>
#include<stdlib.h>
typedef struct BiTNode{
    char data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void CreateBiTree(BiTree &T)
{
    char ch;
    cin>>ch;
    if(ch=='#')
        T=NULL;
    else
    {
        if(!(T = (BiTNode *) malloc(sizeof(BiTNode)))) 
            exit(1);
        T->data=ch;  //生成根结点
        CreateBiTree(T->lchild);  //构造左子树
        CreateBiTree(T->rchild);  //构造右子树
    }
}
void PreOrderTraversal(BiTree T)//先序遍历输出
{
    if(T)
    {
        cout<<T->data;
        PreOrderTraversal(T->lchild);
        PreOrderTraversal(T->rchild);
    }
}
void InOrderTraversal(BiTree T)//中序遍历输出
{
    if(T)
    {
    
        InOrderTraversal(T->lchild);
            cout<<T->data;
        InOrderTraversal(T->rchild);
    }
}
void PostOrderTraversal(BiTree T)//后序遍历输出
{
    if(T)
    {
    
        PostOrderTraversal(T->lchild);
        PostOrderTraversal(T->rchild);
            cout<<T->data;
    }
}
int Depth(BiTree T)//树的深度
{
    if(T==NULL)
        return 0;
    else
    {
        int i=Depth(T->lchild);
        int j=Depth(T->rchild);
        if(i>j)
            return i+1;
        else
            return j+1;
    }

}
int NodeCount(BiTree T)//统计所有结点个数
{
    if(T==NULL)
        return 0;
    else
        return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}
int LeafCount(BiTree T)//统计叶子个数
{ 
    if(T==NULL)
        return 0;
    else if(!(T->lchild||T->rchild))//左右孩子结点都为空则为叶子结点
        return 1;
    else
    {
        return LeafCount(T->lchild)+LeafCount(T->rchild);
    }
}
void PrintLeafNode(BiTree T)//找出叶子结点
{
    if(T)
    {
        if(!(T->lchild||T->rchild))
            cout<<T->data<<" ";
        else
        {
            PrintLeafNode(T->lchild);
            PrintLeafNode(T->rchild);
        }

    }
}
int  main()
{
    BiTree T;
    cout<<"先序遍历输入(以#结束)";
    CreateBiTree(T);
    int n;
    n=Depth(T);
    cout<<"树的深度："<<n<<endl;
    n=NodeCount(T);
    cout<<"结点个数："<<n<<endl;
    n=LeafCount(T);
    cout<<"叶子结点个数："<<n<<endl;
    cout<<"叶子结点为："<<endl;
    PrintLeafNode(T);
    cout<<"\n先序遍历输出：";
    PreOrderTraversal(T);
    cout<<endl;
    cout<<"中序遍历输出：";
    InOrderTraversal(T);
    cout<<endl;
    cout<<"后序遍历输出：";
    PostOrderTraversal(T);
    cout<<endl;
    return 1;
}

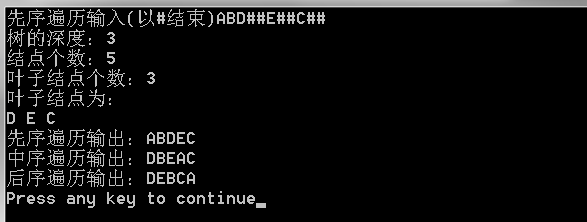
运行结果：