寒假第一周小结
刷题
acwing寒假算法题
https://www.acwing.com/activity/content/88/
算法学习
一、acwing基础算法课
打卡

二、暴力求解法
-
通过问题的分析简单枚举
-
枚举排列、排列生成
<1.通过“求下一个排列”>
点击查看代码
#include<cstdio>
#include<algorithm>//包含next_permutation
using namespace std;
int main(){
int n,p[10];
scanf(“%d”,&n);
for(int i=0;i<n;i++) scanf(“%d ”,&p[i]);
sort(p,p+n); //排序,得到p的最小排列
do{
for(int i=0;i<n;i++) printf(“%d ”,&p[i]);//输出排列p
printf(“\n”);
}while(next_permutation(p,p+n)); //求下一个排列
return 0;
}
<2.解答树>
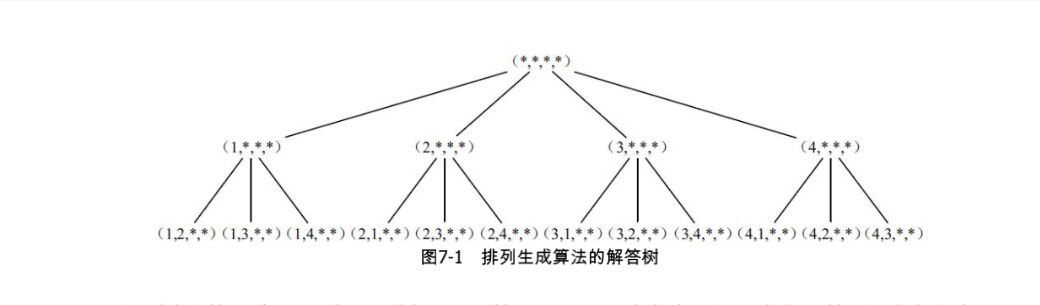

3.子集生成
<1.增量构造法>
点击查看代码
void print_subset(int n,int *A,int cur){
for(int i=0;i<cur;i++) printf("%d ",A[i]);//打印当前集合
printf("\n");
int s=cur?A[cur-1]+1:0;//确定当前元素的最小可能值
for(int i=s;i<n;i++){
A[cur]=i;
print_subset(n,A,cur+1);//递归构造子集
}
}
<2.位向量法>
点击查看代码
void print_subset(int n,int *B,int cur){
if(cur==n){
for(int i=0;i<cur;i++)
if(B[i]) printf("%d",i);//打印当前集合
printf("\n");
return ;
}
B[cur]=1; //选第cur个元素
print_subset(n,B,cur+1);
B[cur]=0; //不选第cur个元素
print_subset(n,B,cur+1);
}
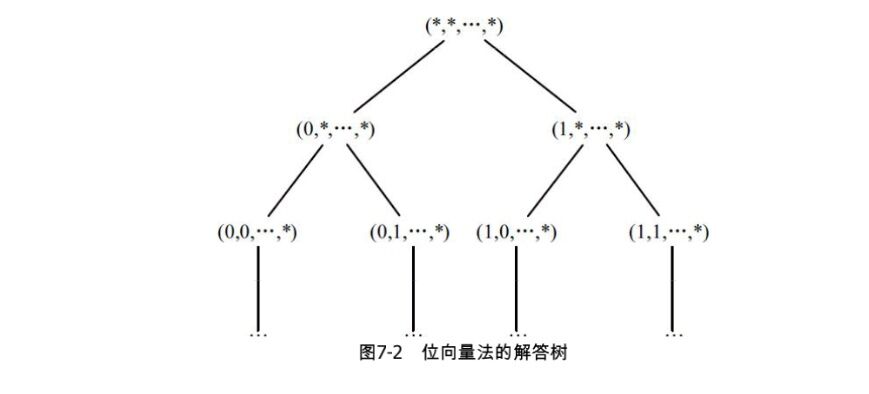
题目:枚举、哈希
二进制和三进制有一位不同,求十进制
点击查看代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;
int get(string s,int b)//将b进制的数转化成十进制
{
int res = 0;
//秦九韶算法
for (auto c: s)
res = res * b + c - '0';
return res;
}
int main()
{
string a,b;
cin >> a >> b;
unordered_set<int> S;
for (auto& c: a)
{
c ^=1;
S.insert(get(a, 2));
c ^=1;
}
for (auto& c:b)
{
char t = c;
for (int i = 0; i < 3;i++ )
if (i + '0' != t)
{
c = i + '0';
int x = get(b, 3);
if (S.count(x))
{
cout << x <<endl;
return 0;
}
}
c = t;
}
return 0;
}
< 3.二进制法 >
"1"存在,"0"不在
<4.回溯法>
典型:
八皇后问题 还不能写出完整代码,只能背模板
点击查看代码
void search(int cur){
if(cur == n) tot++;//递归边界。只要走到了这里,所有皇后必然不冲突//tot解的个数
else for(int i = 0;i<n;i++){
int ok = 1;
C[cur] = i;//尝试把第cur行的皇后放在第i列
for(int j = 0;j < cur;j++)//检查是否和前面的皇后冲突
if(C[cur] == C[j] || cur-C[cur] == j-C[j] ||cur+C[cur] == j+C[j])
{ok=0;break;}
if(ok) search(cur+1);//如果合法,则继续递归
}
}
二维数组的求法,提高程序效率
void search(int cur){
if(cur == n) tot++;
else for(int i = 0;i < n;i++){
if(!vis[0][i] && !vis[1][cur+i] && ! vis[2][cur-i+n]){
//利用二维数组直接判断
C[cur] = i;//如果不用打印解,整个C数组都可以省略
vis[0][i] = vis[1][cur+i]=vis[2][cur-i+n] = 1;//修改全局变量
search(cur+1);
vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n]=0;//!!!改回来
}
}
}
素数环



 浙公网安备 33010602011771号
浙公网安备 33010602011771号