数据结构——八大排序算法(java部分实现)
java基本排序算法
1.冒泡排序
顶顶基础的排序算法之一,每次排序通过两两比较选出最小值(之后每个算法都以从小到大排序举例)图片取自:[小不点的博客](Java的几种常见排序算法 - 小不点丶 - 博客园 (cnblogs.com))
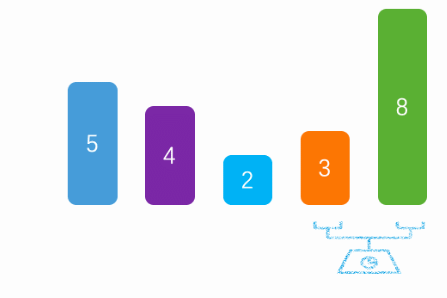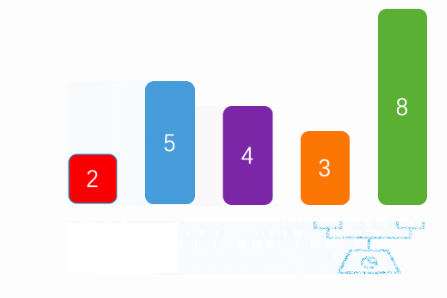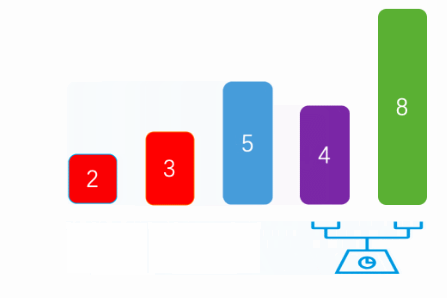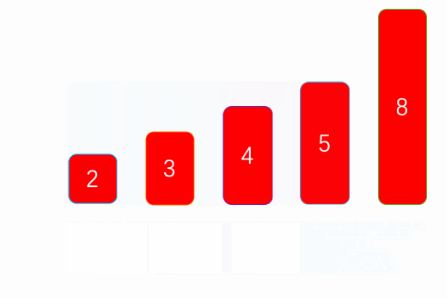
public static void main(String[] args) {
int arr[] = {8, 5, 3, 2, 4};
//外层循环,遍历次数
for (int i = 0; i < arr.length; i++) {
//内层循环一次,获取一个最大值
for (int j = 0; j < arr.length - i - 1; j++) {
//如果当前值比后一个值小,则交换
if (arr[j] < arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
由于是一个双重循环,所以冒泡排序的时间复杂度为O(n²)
2.选择排序
先选择第一个值为默认的最小值并将该元素设置为指针元素,再把这个最小值和它后面的所有元素比较,相当于做了一次固定一个元素的冒泡,如果存在比它小的则交换,遍历一次后选出最小值与当前的指针元素互换,之后在最小值右边的新数组执行同样的操作,直到选出length个“最小值”。
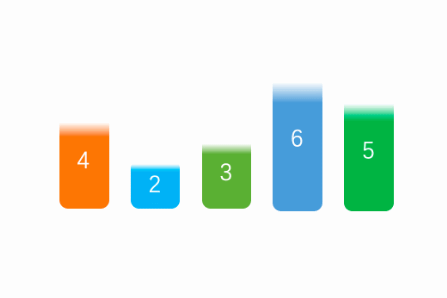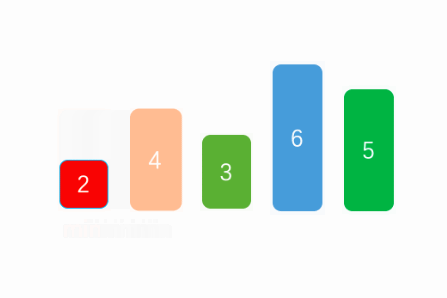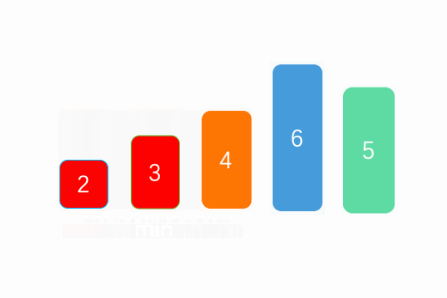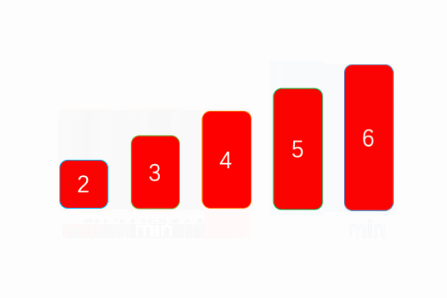
public static void main(String[] args) {
int[] arr = new int[]{1,6,8,5,11,2,15,3,66};
for(int i=0;i<arr.length;i++){
//记录最小值的值和下标,初始化为第一个元素
int min=arr[i];
int index = i;
//遍历一次寻找最小值
for(int j=i+1;j<arr.length;j++) {
//发现有更小的值则交换min和arr[i]的值
if (arr[j] < min) {
min = arr[j];
index = j;
}
}
//交换当前指针元素和"选择"出的最小值的值
int temp = arr[i];
arr[i]=arr[index];
arr[index]=temp;
}
System.out.println(Arrays.toString(arr));
}
跟冒泡排序一样存在双重循环,所以选择排序的时间复杂度为O(n²)
3.插入排序
可以想象成每次向一个有序的子序列里插入一个数并保证序列有序性,算法开始将数组的第一个元素当成有序子序列,第二个元素当成待插入元素,以此类推,该待插入元素会从子序列尾部逐个跟元素比较,直到该元素大于前一个元素为止

public static void main(String[] args) {
int[] arr = new int[]{1, 6, 8, 5, 11, 2, 15, 3, 66};
//外层循环,从第二个数开始逐个插入
for (int i = 1; i <arr.length; i++) {
int insert=i;//记录待插入值的下标
int index = i-1;//记录当前待插入位置
//逐个向前交换,直到子序列升序
while(index>=0&&arr[insert]<arr[index]){
int temp = arr[insert];
arr[insert]=arr[index];
arr[index]=temp;
index--;insert--;
}
}
System.out.println(Arrays.toString(arr));
}
有双重循环,所以插入排序的时间复杂度为O(n²)
4.希尔排序
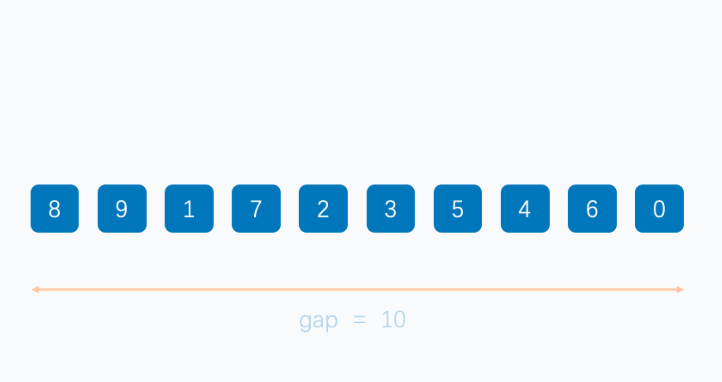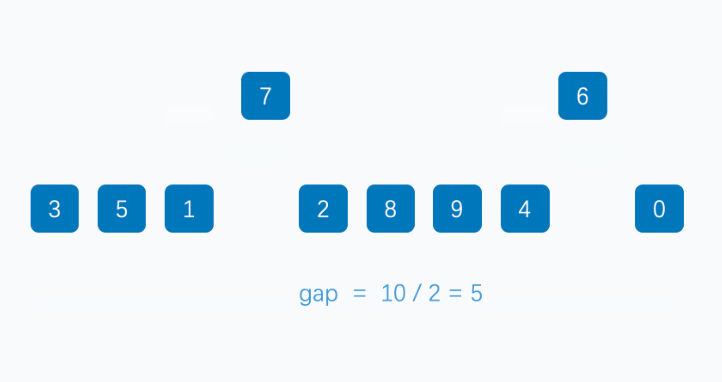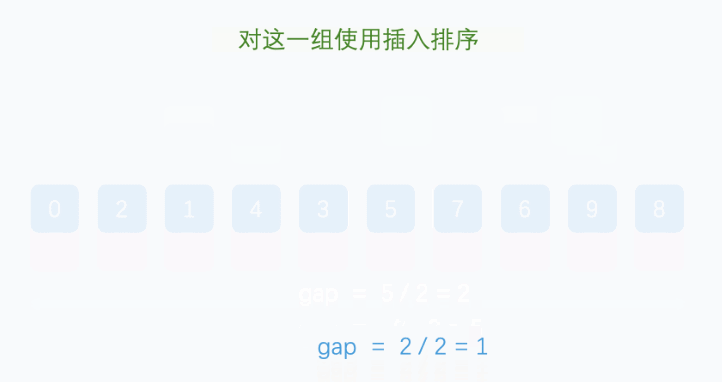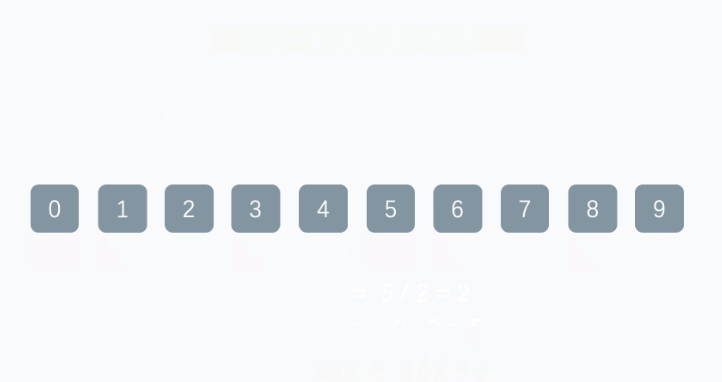
该算法是对插入排序的一种优化算法,它基于分组+排序,设置了一个分组间隔k,一般设置为数组长度的一半,然后从第一个元素开始分组,比如下标为n的元素就和下标为n+k的元素为一组,当数组长度为奇数时,分组1会比其他分组多一个元素,之后在每个分组内进行插入排序,然后对新数组进行分组排序,新间隔为原分组间隔的一半,直到间隔为1,对整个数组进行一次插排结束。
public static void main(String[] args) {
int[] arr = new int[]{1,6,8,5,11,2,15,3,66};
//控制分组间隔,排序步长
for(int i=arr.length/2;i>=1;i/=2){
//控制执行插排的次数
for(int j=i;j<arr.length;j++){
//执行一次步长为i的插入排序
for(int k=j;k>0&&k-i>=0;k-=i){
if(arr[k]<arr[k-i]){
int temp = arr[k];
arr[k]=arr[k-i];
arr[k-i]=temp;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
我在刚开始看到希尔排序的时候,我匪夷所思呀,为什么不直接执行一次插排,而反而折腾了好多次执行了数次插入排序,看起来好像是在做无用功而非是"优化",但实际上当数据量庞大起来后,希尔排序的优势是非常突出的
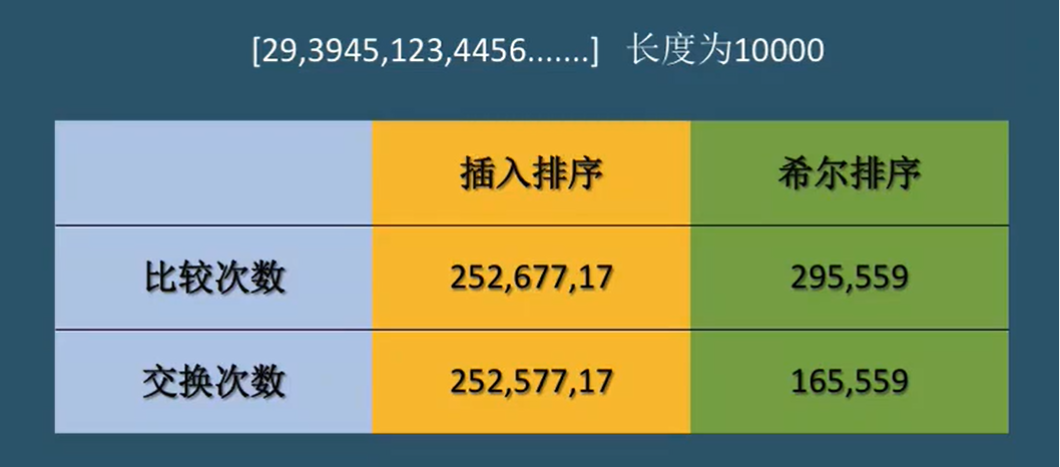
这是某bilibili博主做的一次测试,可以看到希尔排序的次数几乎是指数式的减少的,这是因为,希尔排序避免了插入排序每次都需要从后面开始逐个比较,如果当前数组是一个已经接近有序的序列,那么,插排几乎在做大篇幅的无用功,而希尔排序直接让该元素与"极元素"作比较,不管是在有序还是无序的数组都要优于插排。
平均时间复杂度O(n log n)
5.快速排序
快速排序在定义上时比较好理解的,即随机选取一个"中间数",然后将数组中所有小于中间数的放到中间数的左边,大于的放到右边,然后再对左右子序列执行同样的操作,直到子序列元素为1时,排序完成。
但用算法实现的话比较麻烦,为了节省空间复杂度(当数组规模非常大时,直接copy一份的代价是非常大的),设置了两个指针,low(指向最低位)和high(指向最高位),开始将中间数预存(即此时的low指向的数),high先从右往左扫描,如果high指向的数小于中间数,则将该数赋值给low指向的数组空间,随后low++,之后low从左往右扫描,如果low指向的数大于中间数,则将该数赋值给high指向的空间,随后highj++,high接着扫描,直到low==high,这便递归结束。

public static void main(String[] args) {
int[] arr = new int[]{1,6,8,5,11,2,15,3,66};
int low=0,high=arr.length-1;
fastSort(arr,low,high);
System.out.println(Arrays.toString(arr));
}
public static void fastSort(int[] arr,int low,int high){
if(high-low<1)//如果当前数组只有一个元素,则是有序的
return;
int end =high;//记录当前的高指针的值,用于递归
boolean flag=true;//指示当前该移动哪个指针
int midNumber = arr[low];//默认将第一个元素设置为中间元素
while(true){
if(flag){//移动高指针
if(arr[high]<midNumber){
arr[low++]=arr[high];
flag=false;
}else if(arr[high]>=midNumber)
high--;
}else{//移动低指针
if(arr[low]>midNumber){
arr[high--]=arr[low];
flag=true;
}else if(arr[low]<=midNumber)
low++;
}
if(low==high){
arr[low]=midNumber;
break;
}
}
fastSort(arr,0,low-1);
fastSort(arr,low+1,end);
}
递归开始的判断之所以不用highlow是因为,当子序列是一个一个有序的两个元素的数组时,下次递归将会出现high=-1,low=0的情况,不满足highlow会报出数组下标异常

平均时间复杂度O(n log n)
6.归并排序
归并排序是将数组先拆分在合并的一种算法,具体实现是,先将数组分为单个元素为一组的组别,然后两两合并,合并的时候进行排序,使合并的子序列是有序的,逐层俩俩合并,直到合并成一个完整的数组。

平均时间复杂度O(n log n)
7.堆排序
将待排序序列构造成一个大顶堆(升序建大顶堆,对大顶堆不了解的朋友可以先看看数据结构的二叉树和大小顶堆),此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
如何构造大顶堆呢,先将待排序数组展开为一个完全二叉树,之后从数的第一个非叶子节点开始扫描,扫描顺序由左向右,由下往上,如果发现有子节点大于父节点的情况存在,则调换节点位置,在继续扫描。直到建成大顶堆。
算法平均时间复杂度:O(n log n)
8.基数排序
将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
基数排序按照优先从高位或低位来排序有两种实现方案:
-
MSD(Most significant digital) 从最左侧高位开始进行排序。先按k1排序分组, 同一组中记录, 关键码k1相等, 再对各组按k2排序分成子组, 之后, 对后面的关键码继续这样的排序分组, 直到按最次位关键码kd对各子组排序后. 再将各组连接起来, 便得到一个有序序列。MSD方式适用于位数多的序列。
-
LSD (Least significant digital)从最右侧低位开始进行排序。先从kd开始排序,再对kd-1进行排序,依次重复,直到对k1排序后便得到一个有序序列。LSD方式适用于位数少的序列。
平均时间复杂度:O(d*(n+r)) d 为位数,r 为基数,n 为原数组个数


 浙公网安备 33010602011771号
浙公网安备 33010602011771号